1. 基于皮尔森相关性的相似度 —— Pearson correlation-based similarity
皮尔森相关系数反应了两个变量之间的线性相关程度,它的取值在[-1, 1]之间。当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。
用数学公式表示,皮尔森相关系数等于两个变量的协方差除于两个变量的标准差。
协方差(Covariance):在概率论和统计学中用于衡量两个变量的总体误差。如果两个变量的变化趋于一致,也就是说如果其中一个大于自身的期望值,另一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,则协方差为负值。
标准差(Standard Deviation):标准差是方差的平方根
方差(Variance):在概率论和统计学中,一个随机变量的方差表述的是它的离散程度,也就是该变量与期望值的距离
基于皮尔森相关系数的相似度有两个缺点:
同样的场景在现实生活中也经常发生,比如两个用户共同观看了200部电影,虽然不一定给出相同或完全相近的评分,他们之间的相似度也应该比另一位只观看了2部相同电影的相似度高吧!但事实并不如此,如果对这两部电影,两个用户给出的相似度相同或很相近,通过皮尔森相关性计算出的相似度会明显大于观看了相同的200部电影的用户之间的相似度。
Mahout对基于皮尔森相关系数的相似度给出了实现,它依赖一个DataModel作为输入。
同时,Mahout还针对缺点(1)进行了优化,只需要在构造PearsonCorrelationSimilarity时多传入一个Weighting.WEIGHTED参数,就能使有更多相同评分项目的用户之间的相似度更趋近于1或-1。
- UserSimilarity similarity1 = new PearsonCorrelationSimilarity(model);
- double value1 = similarity1.userSimilarity(1, 5);
- UserSimilarity similarity2 = new PearsonCorrelationSimilarity(model, Weighting.WEIGHTED);
- double value2 = similarity2.userSimilarity(1, 5);
Similarity of User1 and User5 with weighting: 0.9655694890769175
2. 基于欧几里德距离的相似度 —— Euclidean Distance-based Similarity
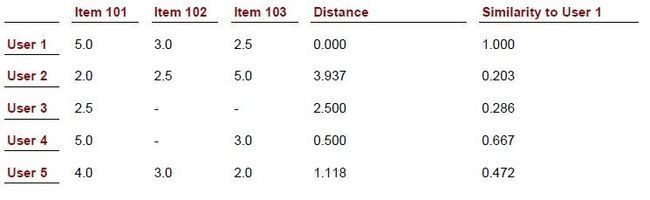
只要至少有一个共同评分项,就能用欧几里德距离计算相似度;如果没有共同评分项,那么欧几里德距离也就失去了作用。其实照常理理解,如果没有共同评分项,那么意味着这两个用户或物品根本不相似。
3. 余弦相似度 —— Cosine Similarity
与欧几里德距离类似,基于余弦相似度的计算方法也是把用户的喜好作为n-维坐标系中的一个点,通过连接这个点与坐标系的原点构成一条直线(向量),两个用户之间的相似度值就是两条直线(向量)间夹角的余弦值。因为连接代表用户评分的点与原点的直线都会相交于原点,夹角越小代表两个用户越相似,夹角越大代表两个用户的相似度越小。同时在三角系数中,角的余弦值是在[-1, 1]之间的,0度角的余弦值是1,180角的余弦值是-1。
借助三维坐标系来看下欧氏距离和余弦相似度的区别:
从图上可以看出距离度量衡量的是空间各点间的绝对距离,跟各个点所在的位置坐标(即个体特征维度的数值)直接相关;而余弦相似度衡量的是空间向量的夹角,更加的是体现在方向上的差异,而不是位置。如果保持A点的位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦相似度cosθ是保持不变的,因为夹角不变,而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征,分别适用于不同的数据分析模型:欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异;而余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦相似度对绝对数值不敏感)。
Mahout没有专门给出基于余弦相似度的实现。
4. 调整余弦相似度 —— Adjusted Cosine Similarity
5. 斯皮尔曼相关 —— Spearman Correlation
斯皮尔曼相关性可以理解为是排列后(Rank)用户喜好值之间的Pearson相关度。《Mahout in Action》中有这样的解释:假设对于每个用户,我们找到他最不喜欢的物品,重写他的评分值为“1”;然后找到下一个最不喜欢的物品,重写评分值为“2”,依此类推。然后我们对这些转换后的值求Pearson相关系数,这就是Spearman相关系数。
斯皮尔曼相关度的计算舍弃了一些重要信息,即真实的评分值。但它保留了用户喜好值的本质特性——排序(ordering),它是建立在排序(或等级,Rank)的基础上计算的。
回顾前面表中User1~5对Item101~103的喜好(评分)值,通过斯皮尔曼相关系数计算出的相似度为:
我们发现,计算出来的相似度值要么是1,要么是-1,因为这依赖于用户的喜好值和User1的喜好值是否趋于“一致变化”还是呈“相反趋势变化"。
- UserSimilarity similarity1 = new SpearmanCorrelationSimilarity(model); // construct a Spearman Correlation-based Similarity
结果:
考虑到Spearman Correlation的效率,可以把SpearmanCorrelationSimilarity包装一层Cache,具体做法为:
- UserSimilarity similarity2 = new CachingUserSimilarity(new SpearmanCorrelationSimilarity(model), model);
这样,每次计算的结果会直接放入Cache,下一次计算的时候可以立即得到结果,而不是重新再计算一次。
6. 基于谷本系数的相似性度量 —— Tanimoto Coefficient-based Similarity
更准确的说法为:Tanimoto Coefficient主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Tanimoto Coefficient只关心个体间共同具有的特征是否一致这个问题。Tanimoto Coefficient又被叫做Jaccard Coefficient,其值等于两个用户共同关联(不管喜欢还是不喜欢)的物品数量除于两个用户分别关联的所有物品数量。
也就是关联的交集除于关联的并集,用公式表示为: