Trie Tree
给你100000个长度不超过10的单词。对于每一个单词,我们要判断他出没出现过,如果出现了,第一次出现第几个位置。
这题当然可以用hash来,但是我要介绍的是trie树。在某些方面它的用途更大。比如说对于某一个单词,我要询问它的前缀是否出现过。这样hash就不好搞了,而用trie还是很简单。
现在回到例子中,如果我们用最傻的方法,对于每一个单词,我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是O(n^2)。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd,那么在他前面的单词中,以b,c,d,f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的,在以a开头中的单词中,我们只要考虑以b作为第二个字母的……这样一个树的模型就渐渐清晰了……
假设有b,abc,abd,bcd,abcd,efg,hii这6个单词,我们构建的树就是这样的。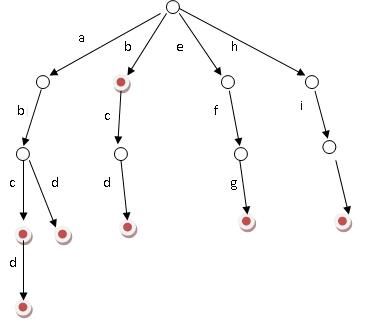
对于每一个节点,从根遍历到他的过程就是一个单词,如果这个节点被标记为红色,就表示这个单词存在,否则不存在。
那么,对于一个单词,我只要顺着他从跟走到对应的节点,再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色,就相当于插入了这个单词。
这样一来我们询问和插入可以一起完成,所用时间仅仅为单词长度,在这一个样例,便是10。
我们可以看到,trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表,或者用数组来模拟动态。空间的花费,不会超过单词数×单词长度。
Problem Description
Ignatius最近遇到一个难题,老师交给他很多单词(只有小写字母组成,不会有重复的单词出现),现在老师要他统计出以某个字符串为前缀的单词数量(单词本身也是自己的前缀).
Input
输入数据的第一部分是一张单词表,每行一个单词,单词的长度不超过10,它们代表的是老师交给Ignatius统计的单词,一个空行代表单词表的结束.第二部分是一连串的提问,每行一个提问,每个提问都是一个字符串.
注意:本题只有一组测试数据,处理到文件结束.
Output
对于每个提问,给出以该字符串为前缀的单词的数量.
Sample Input
banana
band
bee
absolute
acm
ba
b
band
abc
Sample Output
2
3
1
0
用字典树来做:
代码抄于杭电课件上:
Code
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
struct dictree
{
struct dictree *child[26];
int n;
};
struct dictree *root;
void insert(char *source)
{
int len,i,j;
struct dictree *current,*newnode;
len=strlen(source);
if(len==0) return ;
current=root;
for(i=0;i<len;i++){
if(current->child[source[i]-'a']!=0){
current=current->child[source[i]-'a'];
current->n=current->n+1;
}
else{
newnode=(struct dictree *)malloc(sizeof(struct dictree));
for(j=0;j<26;j++)
newnode->child[j]=0;
current->child[source[i]-'a']=newnode;
current=newnode;
current->n=1;
}
}
}
int find(char *source)
{
int i,len;
struct dictree *current;
len=strlen(source);
if(len==0) return 0;
current=root;
for(i=0;i<len;i++){
if(current->child[source[i]-'a']!=0)
current=current->child[source[i]-'a'];
else
return 0;
}
return current->n;
}
int main()
{
char temp[11];
int i,j;
root=(struct dictree *)malloc(sizeof(struct dictree));
for(i=0;i<26;i++)
root->child[i]=0;
root->n=2;
while(gets(temp),strcmp(temp,"")!=0)
insert(temp);
while(scanf("%s",temp)!=EOF){
i=find(temp);
printf("%d\n",i);
}
字典树(Trie)是一种用于快速字符串检索的多叉树结构。其原理是利用字符串的公共前缀来降低时空开销,从而达到提高程序效率的目的。
它有如下简单的性质: (1) 根节点不包含字符信息; (3) 一棵m度的Trie或者为空,或者由m棵m度的Trie组成。 搜索字典项目的方法为: (1) 从根结点开始一次搜索; (2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树 并转到该子树继续进行检索; (3) 在相应的子树上,取得要查找关键词的第二个字母, 并进一步选择对应的子树进行检索。 (4) 迭代过程…… (5) 在某个结点处,关键词的所有字母已被取出,则读取 附在该结点上的信息,即完成查找。2. 实现 (1) 节点#define NUM_CHARS 26
struct Trie_Node {
char* data; // 附加数据
Trie_Node* branch[NUM_CHARS]; // 指针域
int branches; // 存放该节点的后续节点分支数
Trie_Node()
{
data = NULL;
branches = 0;
for( int i=0 ; i<NUM_CHARS ; ++i )
branch[i] = NULL;
};
};
(2) 插入字典项目int Trie::Insert( const char* word , const char* entry )
{
int result = 1, position = 0;
if( root == NULL ) root = new Trie_Node;
char ccode;
Trie_Node *location = root;
while( location!=NULL && *word!=0 )
{
if (*word>='A' && *word<='Z') ccode = *word-'A';
else if (*word>='a' && *word<='z') ccode = *word-'a';
else return 0; // 不合法的单词
if( location->branch[ccode] == NULL )
location->branch[ccode] = new Trie_Node;
location = location->branch[ccode];
position++;
word++;
}
if (location->data != NULL) result = 0;//欲插入的单词已经存在
else
{
location->data = new char[strlen(entry)+1];
strcpy(location->data, entry);
}
return result;
};
(3) 搜索int Trie::Search(const char* word, char* entry ) const
{
int position = 0;
char ccode;
Trie_Node *location = root;
while( location!=NULL && *word!=0 )
{
if (*word>='A' && *word<='Z') ccode = *word-'A';
else if (*word>='a' && *word<='z') ccode = *word-'a';
else return 0;// 不合法的单词
location = location->branch[ccode];
position++;
word++;
}
if ( location != NULL && location->data != NULL )
{
strcpy(entry,location->data);
return 1;
}
else return 0;// 不合法的单词
}
3. 应用 a. HDOJ 1251 统计难题题目请参见:http://acm.hziee.edu.cn/showproblem.php?pid=1251代码实现:#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#define NUM_CHARS 26
class Trie
{
protected:
struct Trie_Node {
char* data;
int branches;
Trie_Node* branch[NUM_CHARS];
Trie_Node()
{
data = NULL;
branches = 0;
for( int i=0 ; i<NUM_CHARS ; ++i )
branch[i] = NULL;
};
};
Trie_Node* root;
public:
Trie() : root(NULL);
int PrefixCount( const char* prefix )
{
int position = 0;
char ccode;
Trie_Node *location = root;
while( location!=NULL && *prefix!=0 )
{
if (*prefix>='a' && *prefix<='z') ccode = *prefix-'a';
else return -1;// 不合法的单词
location = location->branch[ccode];
position++;
prefix++;
}
if ( location != NULL ) return location->branches;
else return 0; // 未找到
};
void CountBranches()
{
this->CountBranches( root );
};
int CountBranches( Trie_Node *start )
{
int sum = 0;
for( int i=0 ; i<NUM_CHARS ; i++ )
if( start->branch[i]!=NULL )
sum += CountBranches( start->branch[i] );
if( start->data != NULL ) sum++;
start->branches = sum;
return sum;
};
int Insert( const char* word , const char* entry )
{
int result = 1, position = 0;
if( root == NULL ) root = new Trie_Node;
char ccode;
Trie_Node *location = root;
while( location!=NULL && *word!=0 )
{
if (*word>='a' && *word<='z') ccode = *word-'a';
else return 0;// 不合法的单词
if( location->branch[ccode] == NULL )
location->branch[ccode] = new Trie_Node;
location = location->branch[ccode];
position++;
word++;
}
if (location->data != NULL) result = 0;//欲插入的单词已经存在
else
{
location->data = new char[strlen(entry)+1];
strcpy(location->data, entry);
}
return result;
};
};
int main()
{
Trie t;
char word[11];
while( true )
{
gets( word );
if( strlen(word)==0 ) break;
t.Insert( word , "S" );
}
t.CountBranches();
while( gets(word)>0 )
printf("%d\n",t.PrefixCount(word));
delete[] word;
return 0;