简介
binary search是一个几乎大家耳熟能详的问题，只要一提到这个问题，似乎立马就有人把代码都浮现在头脑里了。它本质上就是通过不断的折半查找来缩小范围，这样可以达到一个很理想的运行效率。这个方法本身有几个小的地方值得注意。另外，通过binary search引申出来的一些问题也是各种各样，这里也针对两个比较有意思的问题做了一点分析。
binary search的思路和实现
如果用一个比较简单直白的语言来介绍binary search的话，无非就是在一个已经排好序的数组里，通过每次将元素的中间值和目标元素来比较，如果中间值大的话，则在前面部分范围内继续查找，否则在后面的部分继续查找。每次求的这个中位数就将数组分成了两半。这样后面每次查找的范围也就缩小了。假设一个数组的元素有n个，每次执行一个折半元素范围就减少一半。从直观上来看，顶多lgN次的折半也就得到一个结果了。所以，binary search方法的时间复杂度为lgn。
下面是binary search的两个实现：
public static int search(int[] a, int val)
{
int start = 0;
int end = a.length - 1;
int middle;
while(start <= end)
{
middle = start + (end - start) / 2;
if(val > a[middle])
{
start = middle + 1;
}
else if(val < a[middle])
{
end = middle - 1;
}
else
return middle;
}
return -1;
}
public static int recSearch(int[] a, int start, int end, int val)
{
if(start > end)
return -1;
int middle = start + (end - start) / 2;
if(val == a[middle])
return middle;
else if(val > a[middle])
return recSearch(a, middle + 1, end, val);
else
return recSearch(a, start, middle - 1, val);
}
看这些具体的代码，实际上有几个细节是很值得注意的。1. 我们在while循环里面比较的条件是start <= end。 这里一定要把等于的情况也考虑进去。因为有可能在搜索到start == end这一步，我们还是需要判断一下是否和结果相等，否则会漏掉这么一种特殊的情况。2. 在求两个数start, end的中位数的时候，一般我们会笼统的用(start + end) / 2这种方式。但是，在数字比较大的情况下，如果start + end > Integer.MAX_VALUE的话，则会使得首先括号里的运算产生溢出，进而产生不正确的结果。所以为了避免这种情况需要使用start + (end - start) / 2。
引申出来的几个问题
可以说，前面讨论的binary search没什么新奇的，最不济细心看看也就都弄明白了。可是如果在这个问题的基础上结合一些其他情况引申出来的问题，事情就会复杂很多：
问题一：
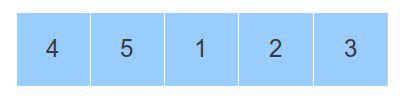
前面我们讨论的binary search是基于所有的元素都是排好序的情况，而且一般是从小到大的顺序。现在考虑一种特殊情况，如果我们有一部分元素循环移位了k个位置，那么和原来的顺序比较可能会有如下的结果：
现在，在这种情况下，如果我们也期望达到logn的元素查找效果的话，该怎么去做呢？根据上图的描述，如果我们将一个递增的数组循环移位若干位的时候，它将会变成一个由两个递增的序列组成的数组。在这两个序列中间是由一个最大值和最小值作为间隔隔开，好像突然间冒出来的一个坎。由于这么个移位，我们如果取数组中间值mid的时候，它可能落在前面那个递增的串上也可能落在后面那个递增的串上。
经过前面这部分的讨论，我们可以得到重要的一点就是，我们对数组取中值，它只可能落在两个递增的串上面。现在，我们再对这两种情况进行讨论：
1. 假定是落在前面的递增串上
按照前面的理解，如果取的中值点能落在前面的串上，则前面这个串至少要涵盖到n/2这么长的长度。也就是说整体的数组移位要超过数组长度的一半。比如下图：
这个时候，如果我们要来查找需要的目标值，可能就需要进行一些比较。由于mid是在前面的递增串中，我们需要看目标值是否正好落在这个递增的范围内，也就是说判断是否val <= a[mid] && val >= a[start]，如果是的，则可以在这个范围内按照二分法的思路继续缩小范围。
同时，我们还要考虑，如果目标值不在这个区域内，那么可能目标值比a[mid]大，也可能目标值比a[start]小。因为mid是落在前面的递增串，它后面的值是可能存在比它更大的。比a[start]小的值也有可能落在后面那个递增的串上。所以，在这种情况下，也就是val < a[start] || val > a[mid]，我们需要在数组的后面部分来搜索目标值。
2. 落在后面的递增串上
落在后面的递增串典型情景如下图：
和前面的讨论类似，我们需要比较目标值是否在后面的递增串内，如果在，则满足val >= a[mid] && val <= a[end]。我们继续在mid和end之间查找。否则，则有val < a[mid] || val > a[end]，对于这种情况，则在start和mid之间查找。
好了，经过前面的这么些讨论，我们知道在这两种情况下的选择。那么，还有一个问题就是，你怎么知道它这个mid值是落在前面的递增串还是后面的递增串呢？通过仔细观察移位后的情况，我们发现，如果a[mid] >= a[start]，则我们可以说明它落在前面的递增串；如果a[mid] <= a[end]，则说明它落在后面的递增串。
有了前面的讨论，我们就可以很容易的写出一个二分搜索方法的变体：
public static int genericSearch(int[] a, int value) {
int start = 0, end = a.length - 1;
int mid;
while(start <= end) {
mid = start + (end - start) / 2;
if(a[mid] == value)
return mid;
if(a[mid] <= a[end]) {
if(value >= a[mid] && value <= a[end])
start = mid + 1;
else end = mid - 1;
} else {
if(value >= a[start] && value <= a[mid])
end = mid - 1;
else start = mid + 1;
}
}
return -1;
}
这里除了上面讨论的地方，还有一个要注意的点就是当里面的元素有相等的情况该如何考虑和处理。实际运行程序的时候，很可能会出现这个时候start == mid或者end == mid的情况。所以，我们在比较的地方判断的时候要加上等号。
还有一个有意思的地方就是，虽然我们是针对数组元素移位的情况进行的讨论，如果我们用一个已经排序的数组运行这一段程序，也可以有效的把元素查找出来。为什么呢？你猜:)
问题二：
给定两个已经排序的数组，求它们的中位数。对于这个中位数，我们的理解可能会存在一定的偏差。一般来说会把这个数字当成一个数组中间的那个元素。比如说[1, 2, 3, 4, 5]，对于它来说，中位数是3。可是对于有偶数个元素的数组呢？它的n/2和n/2 + 1是最中间的两个元素。
实际上，中位数指的是如下的关系：
median = a[n/2 + 1] (如果n为奇数)
median = (a[n/2] + a[n/2 + 1]) /2 (如果n为偶数)
对于奇数个元素来说，它最中间的那个元素确实是使得它两边的元素一样多。而对于偶数个的元素来说，它最中间的是两个元素，所以要取这两个元素的平均值。
基于上述的讨论，假设我们有两个数组[1, 2, 3] [5, 6, 7]，那么它们的中间值则为(3 + 5) / 2 = 4。现在，这个问题就归结为求给定两个数组里的第k个值。我们这里的中间值正好是求第k个值的一种特例。
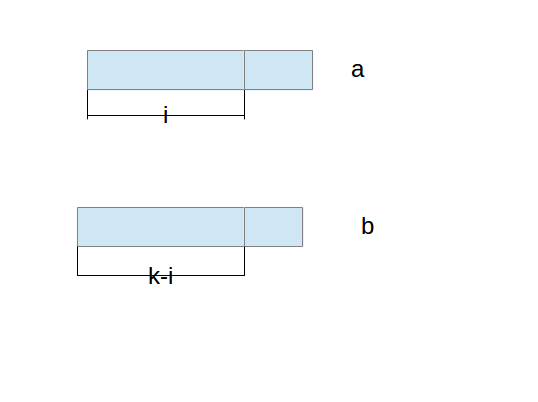
现在，我们就从一个一般的情况来分析取第k个元素的场景。假设我们要取第k个元素的时候，在数组a中间选择的元素点是i，这个i表示的是a中间的第i个，不是索引i。那么，对应的在另外一个数组b中间对应位置的k-i个是我们需要比较的对象。它们的关系如下图：
如果这个时候位置为i的元素，也就是数组a里a[i - 1]的元素大于对应比较的元素，即b[k - i - 1]的元素，这表示至少k-i个元素和ii-1个元素是比我们目前第i个元素小的。如果这个时候，a[i-1]比b[k-i-1]后面那个元素小的话，则表示刚好它就是我们要找的元素。否则我们就要再缩小范围来比较。
我们该怎么来调整这个搜索范围呢？针对这两种情况来讨论，假如a[i - 1] > b[k - i]，这个时候表示a串中第i个元素它在对应的数组b中排到比期望的还要靠后才满足a[i-1] < a[m], m > k - i。所以这个时候我们要找的元素肯定在a[i - 1]的左边范围内。因为在a[i-1]右边的只会更大。这种情况如下：
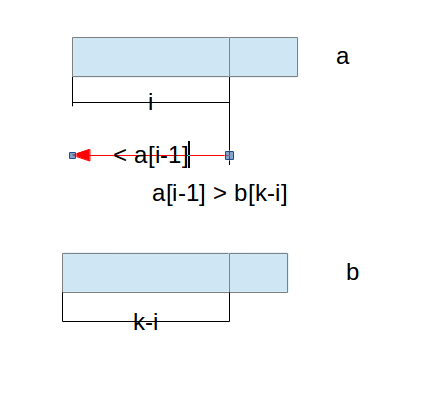对于另外一种情况，就是如果a[i-1] < b[k - i - 1]，那么表示a[i-1]这个元素所大于的元素还不到k个，这个时候需要去看a[i-1]后面的元素，如下图：
按照这边的讨论，我们相当于找到了一个逐步递归的步骤。但是递归的结束条件是什么呢？假设我们已经访问到数组a最小的元素，也就是a[0]了。这个时候，我们只需要直接去看b[k-1]。这里的k-1其实是相对于b数组的起始位置来说的。因为前面的每次递归我们都采用类似二分法的方式将搜索的范围减少一半。另外，如果我们要找的元素为第1个了，这个时候只要比较a[0], b[0]中间两者最小的那个就可以了。这里的a[0], b[0]也是相对位置。
还要一个前面没有澄清的问题，就是我们假设是在数组a中间取到第i个元素。那么最开始我们该设定到哪个位置比较合适呢？随便乱取一个？从二分法的角度来说，我们可以先取k/2个元素，假设a[k/2-1]这个元素也满足> b[k/2-1]并且<b[k/2]的话不就是正好吗？如果没有则按照前面给定的递归关系进行调整。
这个问题最磨人的地方在于它的各种边界条件非常多。这还没完。我们前面是说假设要在a[]里面去取第k/2个元素。可是如果k/2比数组的长度还要大呢？这不是折腾死个人吗？对于这种情况，我们就需要去选择k/2和a[]长度中的最小值。然后再去计算b中间对应位置的元素。所以这部分的逻辑伪代码应该是这样：
pa = Math.min(k / 2, m); // m为a[]的长度 pb = k - pa;
有了前面的这些讨论，我们可以得出如下的代码：
public class Solution {
public double findMedianSortedArrays(int A[], int B[]) {
int m = A.length;
int n = B.length;
int total = m + n;
if(total % 2 == 1)
return findMedian(A, 0, m, B, 0, n, total / 2 + 1);
else
return (findMedian(A, 0, m, B, 0, n, total / 2) +
findMedian(A, 0, m, B, 0, n, total / 2 + 1)) / 2.0;
}
private double findMedian(int[] a, int al, int ar, int[] b, int bl, int br, int k) {
if(ar > br) return findMedian(b, bl, br, a, al, ar, k);
if(ar == 0) return b[bl + k - 1];
if(k == 1) return Math.min(a[al], b[bl]);
int pa = Math.min(k / 2, ar);
int pb = k - pa;
if(a[al + pa - 1] <= b[bl + pb - 1]) return findMedian(a, al + pa, ar - pa, b, bl, br, k - pa);
return findMedian(a, al, ar, b, bl + pb, br - pb, k - pb);
}
}
代码中间有一些细节需要注意。因为每次我们是去计算k/2, m的最小值。然后去比较。如果两个节点的位置不对，要么就是在a[]数组上去看另外一段的位置，这样对应的参数ar, br需要相应的减少pa或者pb。同时，对应的位置查找参数k也要减去相应的pa, pb。
总结
binary search本身的思想比较简单，可是由它引申出来的问题可以有很多。对于第二个问题，目前的理解和表示还是不够深刻，后续会继续完善对它的表述。
参考资料
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=binarySearch