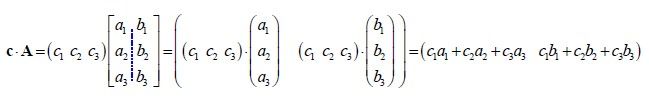线性代数与几何的关系：一方面几何是线性代数的描述，而另一方面线性代数是几何的推导
f(x) = T*x ：这是一个典型的1D的线性函数，T是该函数的算子。它的几何意义是：以X为轴的1维点x的集合到以Y为轴的1维点y的集合的映射。而T就是其映射条件，T也是一个1D的矩阵。这样看来其实我们写程序的每一个函数都相当于一次映射，只不过返回的结果和输入的参数的维度不一定一样。
从1D推向3D：f(x,y,z) = T*(x,y,z) 此时的T是一个3D的转换矩阵，而我们模型的点，从世界坐标映射到视图坐标，转换矩阵Tv即相当于这两个空间的一次转换。
向量的几何意义：
1.向量的点积：
a⋅b = |a|*|b|*cos(o) = a1*b1 + a2*b2 +..+an*bn; 对位向乘。几何意义：向量内积的几何解释就是一个向量在另一个向量上的投影的积。
2.向量的叉积：
a X b = |a||b|sin(o)*N= (a2*b3 - a3*b2, a3*b1-a1*b3, a1*b2-a2*b1) ：N为垂直于aXb平面的向量。它最大的意义就是求面的单位法向量。
3.向量的单位向量表示：
ab = a*b + aXb ：ab为向量的直积，就是两个向量的矩阵乘法，a的每个数跟b的每个数乘。
4.向量的逆运算：已知向量a和a*b的结果K，aXb的结果c，可以求出b来。这里需要列方程式：
a*b = K ，aXb = c ，-----> b = (K*a - aXc)/a*a ：特殊时候还是可以通过这种方式做逆运算的
5.向量与矩阵的关系：一个n维向量是一个 1n矩阵。
矩阵：
1.矩阵的加法：
A+B ：对位相加 A+n ：n和A的每一位对应相加 n*A n和A的每一位进行相乘。
2.矩阵与向量的乘法：
从几何意义上来讲，相当于矩阵对向量进行空间映射。从数学意义上来讲，可以把向量当做一个1n矩阵如果向量在左，可以把向量当做一个n1矩阵，如果向量在右。
向量与矩阵乘法的特殊用途：
(1,0,0)*A ：把矩阵A的第“1”所在的行取出来，这里是第一行。
A*(1,0,0) ：把矩阵的第“1”所在的列取出来，这里是第一列。
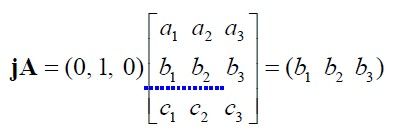
此外jA 单位向量左乘矩阵还有一种用途，就是求转换矩阵。例如，已知法线空间的三个单位向量在世界空间的坐标。想求法线空间转换到世界空间的矩阵真心容易，上述就是法线空间的单位向量根据转换矩阵，转换到世界空间。所以求转换矩阵的时候，只需要把世界空间的3个坐标按顺序放置就行了。
3.特殊矩阵与向量乘：
(1)旋转矩阵：
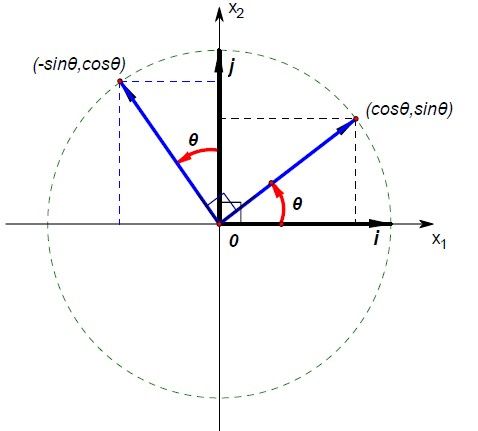
从上面可知，其实想求出转换矩阵，只需要知道单位坐标系矩阵，对应的转换结果就行了。而旋转很容易理解从上图：（注意旋转是逆时针的）
4.矩阵之间相乘：尽管矩阵可以看做是一组向量，但是这里把相乘的矩阵都当做转换因子来看待。那么，矩阵向乘的几何意义就是转换的累积，在做骨骼动画的时候，会用到这一点来反应每一个关键的位置和方向的变化。由于矩阵*矩阵是对原始向量的累积变换，那么，矩阵的幂就相当于多次使用同一个矩阵进行累积转换。
设
为
距阵，
为
距阵，则矩阵 
可以左乘矩阵 
（注意：距阵
的列数等与矩阵 
的行数），所得的积为一个 
距阵
，即
这里有一个左乘的概念，而且乘后的结果不一定跟两个因素的类型相同，41x14 = 44，同样14x41 = 11，所以在乘的时候需要自己先对乘后结果的维度有谱。
单元矩阵乘任何矩阵等于任何矩阵。
左乘：前面的矩阵的每一列跟后面的矩阵的每一行相乘。
5.转置矩阵：如果两个A和B矩阵互为转置，就是前面A的行对应后面B的列。矩阵的转置很常用，但是其作用也就是改变乘积的顺序，并无特殊的几何意义。
6.逆矩阵：我们知道，矩阵是用来把向量从一个系变换到另一个系的算子，而逆矩阵就是把向量从另一个系又转换回来的矩阵。矩阵乘逆矩阵 = 单位矩阵。
逆矩阵的性质：
如果M是非奇异矩阵，则该矩阵的逆的逆等于原矩阵：(M-1)-1=M.
单位矩阵的逆势它本身：I-1=I
矩阵转置的逆等于它逆的转置：(MT)-1=(M-1)T
矩阵乘积的逆等于矩阵的逆的相反顺序的乘积：(AB)-1= B-1 A-1
正交矩阵：若方阵M是正交的，则当且仅当M与它转置MT的乘积等于单位矩阵。MMT=I.
如果一个矩阵式正交的，那么它的转置等于它的逆：MT= M-1。
若一个矩阵是正交的，它必须满足：
矩阵的每一行都是单位向量。
矩阵的所有行都相互垂直。