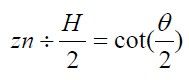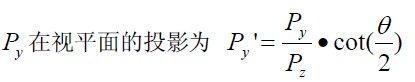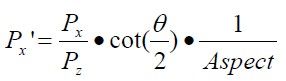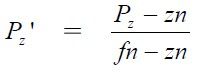基础转换矩阵:3D 基础矩阵推导 矩阵的变换是线性代数的基础,也是图形相关的技术的基础,如果做好图形渲染,仅仅了解这些基础是远远不够的。还需要比较清楚的是3D中的6次向量空间的变换的几何意义,以及变换矩阵的推导。
向量空间转换和顶点坐标转换的区别:其实没区别都是把顶点从一个坐标空间转换到另一个。只不过模型的转换只针对模型本身,例如模型转换到世界空间,你可以说它是从模型空间转换到世界空间,也可以说它就是模型在世界空间里面的转换,因为世界中的所有模型转换的规则并不全都一样。但是,模型从世界空间转换到视图空间就是空间坐标系的转换了,因为空间里面的所有顶点的转换规则都一样。
视点变换矩阵:
世界空间(World Space)转换到视图空间(Eye Space)的矩阵
// Lookat 表示是view转换矩阵 LH 是左手系
// pEye 摄像机的坐标位置 pAt 前方,这也算是一个方向向量了
// pUp 上方也是一个方向向量
D3DXMATRIX* WINAPI D3DXMatrixLookAtLH ( D3DXMATRIX *pOut, CONST D3DXVECTOR3 *pEye, CONST D3DXVECTOR3 *pAt, CONST D3DXVECTOR3 *pUp );
方法体的实现:
zaxis = normal(At - Eye)
xaxis = normal(cross(Up, zaxis))
yaxis = cross(zaxis, xaxis)
xaxis.x yaxis.x zaxis.x 0
xaxis.y yaxis.y zaxis.y 0
xaxis.z yaxis.z zaxis.z 0
-dot(xaxis, eye) -dot(yaxis, eye) -dot(zaxis, eye) 1
1.pEye是视点的位置,也就是摄像机的位置,pAt是一个视角方向上的一个点,而不是描述视角方向的方向向量,这是因为
zaxis = normal(At - Eye) 方法向量是通过 At - Eye 计算出来的,而不是直接为at。
2.蛋疼的是Up又是一个方向向量,因为xaxis = normal(cross(Up, zaxis)),两个向量的叉乘能够得到他们的法向量。这里利用的是up和zaxis 组成的是一个垂直的平面,而它的法向量肯定是指向xaxis x轴了。
3.cross(zaxis, xaxis)根据已知的两个轴求出第三个轴来,我这里有个疑问up难道不跟yaxis 相等吗?或许这里强调的是一种更灵活的操作,就是up它只是在yz平面上,但并不要求它与zaxis 垂直。
4.我们知道3x3矩阵只是对顶点做了相应的旋转和缩放,而-dot(xaxis, eye) -dot(yaxis, eye) -dot(zaxis, eye)则是对位置的移动,保证世界坐标的原点移动到视图坐标的原点,也就是相机的位置。
5.视点变换矩阵的获取:
void CameraControl::updateView()
{
float3 up, position, lookAt;
float yaw, pitch, roll;
D3DXMATRIX rotationMatrix;
position = mBean.position;
lookAt = mBean.lookAt;
up = mBean.up;
pitch = mBean.angleX;
yaw = mBean.angleY;
roll = 0;
// 1.根据旋转因子,获取旋转矩阵 angleX,angleY,这里不以z为轴进行旋转
D3DXMatrixRotationYawPitchRoll(&rotationMatrix, yaw, pitch, roll);
// 2.这里对两个方向向量进行旋转
D3DXVec3TransformCoord(&lookAt, &lookAt, &rotationMatrix);
D3DXVec3TransformCoord(&up, &up, &rotationMatrix);
// 3.这个完全是因为LookAtLH的参数不是方向向量而是一个点
lookAt = position + lookAt;
// Finally create the view matrix from the three updated vectors.
D3DXMatrixLookAtLH(&mView, &position, &lookAt, &up);
}
透视投影矩阵的推导:
投影空间:在投影空间中,视图空间的视锥变成为一个长方体,首先这里视图空间本身是一个与世界空间一样的大空间,它也不是被截成了一个视锥。只不过转换到投影空间的,只是视图空间里的视锥部分的内容。视图空间到投影空间的转换,主要是把透视空间椎体里面的内容转换到投影空间,投影空间本身是一个矩形的。
矩形的左裁剪面为x = -1,右为x = 1,上为 y = 1,下为 y = -1,近裁剪面为 z = 0 (这里是0不是-1,这个主要是对应深度模板来的),远裁剪面为 z = 1。
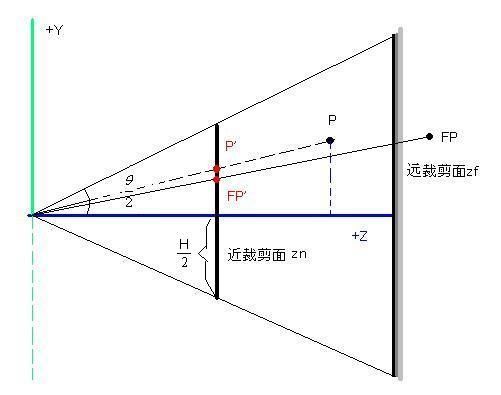
从这个图可以看出P是视锥里面的一个点,而P1是映射到近裁剪面的一个点,最终P在透视空间里面的结果Pt为(P1.x,P1.y,P.z)当然还要对Pt进行缩放,使其比例为上面说道的(1,1,0),(-1,-1,-1)这个矩阵里面。
如图,现在已知Py,Pz和近裁剪面zn求P1y。 P1y/zn = Py/Pz,所以最终结果为:
然后把这些式子转换成矩阵:
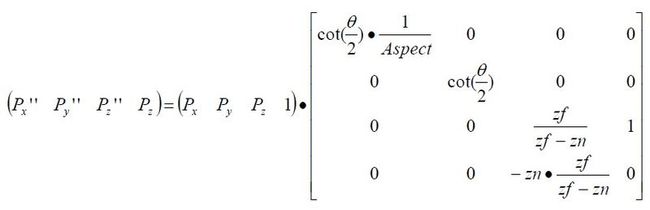
视图空间转换到透视空间,做了两件事,一个是等比例缩放,把视锥缩放到一个矩形里面,然后就是调整比例,把比例调整到一个(1,1,0)(-1,-1,-1)里面。
需要注意的是:此转换没有对结果进行归一化。
// fovy 投影角度 Aspect 宽和高的比率 zn 近截面的z值 zf 远截面的z值 D3DXMATRIX* WINAPI D3DXMatrixPerspectiveFovLH ( D3DXMATRIX *pOut, FLOAT fovy, FLOAT Aspect, FLOAT zn, FLOAT zf );
屏幕空间:
从透视空间转换到屏幕空间的这个过程,是在光栅化的时候进行的,所以,你在PS里面获取到的float4 piPosition : SV_POSITION;这个顶点位置信息已经不是透视空间里的了。所以,如果想获取透视空间的position请不要使用SV_POSITION这个语义来进行描述。
总结:
1.在所有需要变换的内容当中,有顶点和向量之分,对于顶点来说位置的移动是有意义的,而对于向量来说,位置的移动反而会改变向量的方向。原则上来说,位置使用4x4矩阵进行转换,而向量用3x3的矩阵进行转换,因为第四行和第四列是用于平移的。
2.摄像机位置和方向,光源的位置和方向,是不需要进行世界矩阵变换的,因为他们本身就是身处世界空间之中。这个如果不清楚,很容易在VS里面乘一个世界转换矩阵。当然,也有特殊情况,就是你的模型够复杂,并且里面有相对模型不变的光源,这个时候光源的位置是模型空间的,那么在转换的时候是需要进行世界坐标转换的。从这里可以看出,事无绝对,最根本的还是得清楚你在干什么。
3.原则上来说,对于一些类似光照计算,或者其他的会用到顶点位置信息或光源,摄像机的信息的计算。都应该在世界空间,或者视角空间里面进行处理。因为这个时候,顶点之间的相对位置没有异变,放在透视空间或者屏幕空间会使结果不可控。
4.所有D3DX的工具方法,都是这样一个原则:1.左手系,2.顺时针为正,3.向量*矩阵。它对应了最终描述的结果。
5.在使用基础矩阵进行转换的时候:先平移,再旋转,后缩放。
6.每次转换过方向向量后,都有必要对其进行归一化。
7.通过D3DX提供的方法获取的世界矩阵,视图矩阵,透视矩阵,在shader里面转换顶点前都需要进行转置,这是我最费解的地方。不是说好了,左手系,向量*矩阵的么,为啥用的时候还需要进行一次转置呢?先这样做吧 - -。
网上的一段文字,难道方向向量,非等比例缩放也不行吗?
之前看过一些文章,说道mesh顶点的空间变换,从本地坐标系变换到世界坐标系,位置信息是乘以世界矩阵,而点的法向量要变换到世界空间下,是要乘以世界矩阵的逆矩阵的转置矩阵。网上有关于这样做的证明。只是之前在项目中,一开始我并不知道要这样做,都是乘以世界矩阵,但是用于光照方程,或者说计算球形贴图坐标的时候,也并没有出错,最后的效果都是满意的,疑惑了很久。
最近翻看《实时计算机图形学》一说,才明白其中原因。因为项目中我用到的世界矩阵中,大部分都是只包括了平移信息和旋转信息,没有去做scale的变换,都是1:1的比例在绘制。问题就在这里,因为法向量是一个方向向量,不是矢量,在变换的过程中,把法向量变为齐次坐标的时候,W分量要设置为0,也就是忽略了平移变换。所以这个世界矩阵就可以看成是一个3*3的旋转举证,而所有的旋转矩阵都是正交矩阵。正交矩阵有一个特性,就是正交举证的逆矩阵等于他的转置矩阵。所以正交矩阵的逆矩阵的转置矩阵就是正交矩阵的转置矩阵的转置矩阵,也就是正交矩阵自己(上面一段话很绕口啊)!
所以,这时候的世界矩阵的逆矩阵的转置矩阵就是世界矩阵,所以我得到了想要的结果。如果出现了scale信息,且各个轴不是1:1的比例的话。这时候的世界矩阵就不能算是正交的,就会出现问题。