有限记忆程序与有限状态换能机器

有限记忆程序与有限状态换能机器

译自：《 An Introduction to the Theory of Computation 》by Eitan Gurari

刘建文略译（ http://blog.csdn.net/keminlau ）

KEY:信息处理 计算理论 形式语言 编程语言

Preface

计算（Computations）是为解题而设计的。程序（Programs）是描述计算的载体，机器（computers）是执行程序的装置。计算机科学领域关注两个对象——程序和机器。“程序”包括研究程序设计的方法论，比如算法、数据结构和编译原理等；“机器”包括研究执行程序的机器的开发方法，比如操作系统（KEMIN:OS了实现虚拟机器，机器涵盖了机器指令及其操作的数据的性质）。因此可得，程序、机器、问题（problems）和计算是计算机科学的核心课题，全面厘清它们的性质非常重要。性质包括属性和关系。

本书探索与程序、机器、问题和计算相关的一些重要概念。这些探索会转为对数学理论和模型的研究，比如自动机和形式语言。理论和模型提供一种简便的研究手段，因为理论和模型忽略不相关的细节。

Chapter 2 studies finite-memory programs. The notion of a state is introduced as an abstraction for a location in a finite-memory program as well as an assignment to the variables of the program. The notion of state is used to show how finite-memory programs can be modeled by abstract computing machines, called finite-state transducers.

第二章探讨有限记忆的程序（finite-memory programs）。状态（state）的概念被用来对有限记忆程序内的位置（location ）进行抽象和对程序的变量的赋值（assignment ）的抽象。状态的概念是用来展示如何将有限记忆的程序建模成一种抽象计算机 ，叫有限状态换能器（transducers）。（有关于信息与状态的更多内容看这里 。）

The transducers are essentially sets of states with rules for transition between the states. The inputs that can be recognized by finite-memory programs are characterized in terms of a class of grammars, called regular grammars. The limitations of finite-memory programs, closure properties for simplifying the job of writing finite-memory programs, and decidable properties of such programs are also studied.

换能器的本质是一集状态和转换该集状态的操作规则的[组合 ]。有限记忆程序的输入（或者有限状态换能器所识别的语言）由一种特定的语法来刻画，这种语法叫正则语法（regular grammars）。有限记忆程序的局限、简化编写有限记忆程序的闭包性质（closure properties）和有限记忆程序的可判定性（decidable properties）在本章也被探讨。

第三章……

Chapter 2 FINITE-MEMORY PROGRAMS

Finite-memory programs are probably one of the simplest classes of programs for which our study would be meaningful.

1. 1. The first section of this chapter motivates the investigation of this class.
2. 2. The second section introduces the mathematical systems of finite-state transducers, and shows that they model the computations of finite-memory programs.
3. 3. The third section provides grammatical characterizations for the languages that finite-memory programs accept, and
4. 4. the fourth section considers the limitations of those programs.
5. 5. The fifth section discusses the importance of closure properties in the design of programs, and their applicability for finite-memory programs.
6. 6. And the last section considers properties that are decidable for finite-memory programs.

2.1 Motivation

It is often useful when developing knowledge in a new field to start by considering restricted cases and then gradually expand to the general case. Such an approach allows a gradual（逐渐的, 徐徐的, 渐增的 ） increase in the complexity of the argumentation（争论, 论证, 论点, 讨论 ）. In particular, it is a quite common strategy in the investigation of infinite systems to start by considering finite subsystems. We take a similar approach here by using programs with finite domains of variables, called finite-memory programs or finite-domain programs, first.

每当我们进入一个新研究领域时，“先[特殊]后[一般]”的方法很管用。所谓“先[特殊]后[一般]”是指，我们先研究该领域的特殊现象的例子，再进一步通过抽象上升到通用的一般的现象例子。为什么这个种方法管用？因为一开始新领域给我们的信息是缺乏的，并且很可能是不全面的，冰山一角是很难拨开复杂现象背后那一般性的本质的。而透过特殊例子，我们可以对复杂事物有直接的相对完整的切片式的感性认识，然后再逐步增加特殊例子的复杂度，操作方法是调整现象产生的环境参数，认识第二个特殊例子（复杂的复就是重复），并与第一个特殊例子进行比较，找出相同处与不同处，反复这个过程，直到牢牢掌握复杂现象的本质。同样的模式也适用于用作研究无限系统的策略，就是透过研究无限系统的有限情况着手。

如何确定相对完整的[特殊例子]？确定它又有什么用？

这个似乎比较难把握，因为事物联系是连续的，没有明显的断层；要相对多完整取决于你研究的深度和广度。

特殊例子具体有些什么内容？

这个更难了，先确定变量X是什么，再确定X的取值范围；

我们取用后一种模式来研究程序（program），先考虑程序在变量可取有限值的（finite domains of variables）情况着手，这种程序叫[有限记忆程序]（finite-memory programs）或[有限域程序]（finite-domain programs）。举一些有限记忆程序的例子：

第一，词法分析器

编译器的词法分析器就是一个有限记忆程序，它主要的任务是扫描源码输入，对源码的符号进行分拣归类。

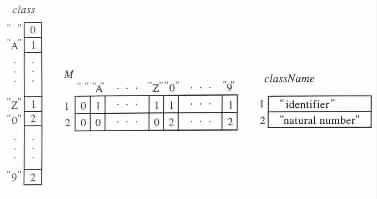
Example 2.1.1 Let LEXANL be the finite-memory program in Figure 2.1.1(a).

Figure 2.1.1(b)

程序的域假定等于 {" ", "A", . . . , "Z", "0", . . . , "9", 0, 1, 2}, 其中 " " 为初始值；函数class, className, and M 由表Figure 2.1.1(b) 定义。

词法分析程序LEXANL 对输入的标号（tokens）进行判断，分类成标识符和自然数。标识符起始于一个字母，后跟任意字母或数字；自然数则一个或多个数字组成；标号间以一个或多个空格符分隔。

可以很简单地修改函数class, className, 和M的定义来扩展LEXANL 的标号识别功能。

第二，通信协议

Protocols for communicating processes are also examples of systems that are frequently
designed as finite-memory programs. In such systems, each process is represented by a finite-memory program. Each channel from one process to another is abstracted by an implicit queue, that is, by a first-in-first-out memory. At each instance the queue holds those messages that have been sent through the channel but not received yet. Each sending of a message is represented by the writing of the message to the appropriate channel. Each receiving of a message is represented by the reading of the message from the appropriate channel.

自然现象的数学建模方法论

FSM, as a mathematical modeling methodology, can be used to describe physical phenomena as well as abstract concepts When FSM is used to describe one complicated system, the systematic model are abstracted as a “black-box”, whose input and output are only observable

有限记忆程序有一些有趣的可判定性质

In Section 2.6 it is shown that finite-memory programs have some interesting decidable properties. Such decidable properties make the finite-memory programs also attractive as tools for showing the complexity of some seemingly unrelated problems.

有限记忆程序有多少？什么东西有限？真的很有限？

Computer programs that use no auxiliary memory, except for holding the input and output values, are by definition examples of finite-memory programs. However, such programs can deal with domains of high cardinality（基数性） (i.e., 2^k for computers with k bits per word), and as a result their designs are generally not affected by the finiteness of their domains. Consequently, such programs should not generally be considered as "natural" finite-memory programs.

2.2 Finite-State Transducers

Central to the investigation of finite-memory programs is the observation that the set of all the states reachable in the computations of each such program is finite. As a result, the computations of each finite-memory program can be characterized by a finite set of states and a finite set of rules for transitions between those states.

那到底有限记忆程序主要研究什么重要的内容？答案是[有限记忆程序]在计算操作过程所能到达的状态全集，这个集合是有限的。因此，有限记忆程序的[计算性质 ]可以由[有限的状态集 ]和[有限的状态转换规则集 ]完全描述。

Abstracted Finite-Memory Programs

Specifically, let P be a finite-memory program with m variables x1, . . . , xm, and k instruction segments I1, . . . , Ik. Denote the initial value of the variables of P with Θ.

Each state of P is an (m + 1)-tuple [i, v1, . . . , vm], where i is an integer between 1 and k, and v1, . . . , vm are values from the domain of the variables. Intuitively, a state [i, v1, . . . , vm] indicates that the program reached instruction segment Ii with values v1, . . . , vm in the variables x1, . . . , xm, respectively.

假设P是一支有限记忆程序，P有m个变量 x1, . . . , xm, 和k条指令（instruction segments）I1, . . . , Ik，变量的初始值均为Θ。
那么P的状态是一个 (m + 1)元组 [i, v1, . . . , vm]，其中，i 取值于1到k之间的整数，v1, . . . , vm取值程序域。
很显然的，状态[i, v1, . . . , vm]表明了程序P到达了指令Ii ，并且各变量（v1, . . . , vm）分别取值为x1, . . . , xm。

The computational behavior of P can be abstracted by a formal system <Q, ∑, Δ, δ, q0, F>, which is defined through the algorithm below. In the formal system
Q ：represents the set of states that P can reach.
δ：represents the set of transitions that P can take between its states.
∑：represents the set of input values that P can read.
Δ：represents the set of output values that P can write.
q0：represents the initial state of P.
F ：represents the set of accepting states that P can reach.

程序P的[计算行为（computational behavior ）]可用一形式系统<Q, ∑, Δ, δ, q0, F>来描述，系统各元素的定义：
KEMIN:注意，是对程序的动态行为进行刻画和描述，而且用到了形式系统，这种定义方式跟一般对静态概念的的定义形式不一，本质却是一样的。
Q ：程序P能到达的状态集合
δ：程序P的状态转换规则集
∑：程序P的输入的集合
Δ：程序P的输出集合
q0：程序P的初始状态
F ：程序P的接受状态的集合

以上形式系统的元素：Q, ∑, Δ, δ, q0, F的具体定义可以通过以下的步骤来一步一步的确定：(original:http://blog.csdn.net/keminlau/archive/2009/12/19/5039826.aspx)

The algorithm determines the sets Q, , , , and F by conducting a search for the elements of the sets.

• Step 1 Initiate Q to the set containing just q0 = [1,Θ , . . . ,Θ ], and δ to be an empty set. q0 is called the initial state of P, and δ is called the transition table of P.
• Step 2 Add the state p = [j, u1, . . . , um] of P to Q, if for some state q = [i, v1, . . . , vm] in Q the following condition holds: P can, by executing Ii with values v1, . . . , vm in its variables, reach Ij with u1, . . . , um in its variables, respectively.
• Step 3 Add (q, , (p, )) to , if P, by executing a single instruction segment, can go from state q in Q to state p in Q while reading and writing . For notational convenience, in what follows (q, , (p, )) will be written as (q, , p, ). Each tuple in is called a transition rule of P.
• Step 4 Repeat Steps 2 and 3 as long as more states can be added to Q or more transition rules can be added to .
• Step 5 Initialize , , and F to be empty sets.
• Step 6 If (q, , p, ) is a transition rule in and then add to . Similarly, if (q, , p, ) is a transition rule in and , then add to . Each in is called an input symbol of P, and is called the input alphabet of P. Similarly, each in is called an output symbol of P, and is called the output alphabet of P.
• Step 7 Insert to F each state [i, v1, . . . , vm] in Q for which Ii is a conditional accept instruction. The states in F are called the accepting , or the final , states of P.

By definition δ is a relation from Q × (∑∪{ε}) to Q × (Δ∪{ε}). Moreover, the sets Q, ∑, Δ, δ, q0, F are all finite because the number of instruction segments in P, the number of variables in P, and the domain of the variables of P are all finite.

Finite-State Transducers

In general, a formal system M consisting of a six-tuple <Q, , , , q0, F> is called a finite-state transducer if it satisfies the
following conditions.
Q is a finite set, whose members are called the states of M.
is an alphabet, called the input alphabet of M. Each symbol in is called an input symbol of M.
is an alphabet, called the output alphabet of M. Each symbol in is called an output symbol of M.
is a relation from Q × ( { }) to Q × ( { }), called the transition table of M. Each tuple (q, , (p, )), or simply (q, , p, ), in is called a transition rule of M.
q0 is a state in Q, called the initial state of M.
F is a subset of Q, whose states are called the accepting , or the final , states of M.

Configurations and Moves of Finite-State Transducers

Intuitively, a finite-state transducer M = <Q, , , , q0, F> can be viewed as an abstract computing machine. The computing
machine consists of a finite-state control, an input tape, a read-only input head, an output tape, and a write-only output head
(see Figure 2.2.4).

Computations of Finite-State Transducers

The computations of the finite-state transducers are defined in a manner similar to that for the programs. An accepting
computation of a finite-state transducer M is a sequence of moves of M that starts at an initial configuration and ends at an
accepting configuration. A nonaccepting , or rejecting, computation of M is a sequence of moves on an input x for which the
following conditions hold.
a. The sequence starts from the initial configuration of M on x.
b. If the sequence is finite, then it ends at a configuration from which no move is possible.
c. M has no accepting computation on x.
Each accepting computation and each nonaccepting computation of M is said to be a computation of M.

Relations and Languages of Finite-State Transducers

The relation computed by a finite-state transducer M = <Q, , , , q0, F>, denoted R(M), is the set { (x, y) | (q0x, ) * (xqf, y)
for some qf in F }. That is, the relation computed by M is the set of all the pairs (x, y) such that M has an accepting computation
on input x with output y.
The language accepted , or recognized, by M, denoted L(M), is the set of all the inputs that M accepts, that is, the set { x | (x, y)
is in R(M) for some y }. The language is said to be decided by M if, in addition, M halts on all inputs, that is, on all x in *.
The language generated by M is the set of all the outputs that M has on its inputs, that is, the set { y | (x, y) is in R(M) for some
x }.

From Finite-State Transducers to Finite-Memory Programs

The previous discussion shows us that there is an algorithm that translates any given finite-memory program into an equivalent finite-state transducer, that is, into a finite-state transducer that computes the same relation as the program. Conversely, there is also an algorithm that derives an equivalent finite-memory program from any given finite-state transducer. The program can be a "table-driven" program that simulates a given finite-state transducer M = <Q, , , , q0, F> in the manner described in Figure 2.2.10.

It follows that the finite-state transducers characterize the finite-memory programs, and so they can be used for designing and analyzing finite-memory programs. As a result, the study conducted below for finite-state transducers applies also for finite-memory programs.
Finite-state transducers offer advantages in
a. Their straightforward graphic representations, which are in many instances more "natural" than finite-memory programs.
b. Their succinctness, because finite-state transducers are abstractions that ignore those details irrelevant to the study
undertaken.
c. The close dependency of the outputs on the inputs.