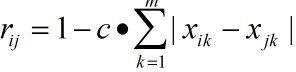基于模糊等价关系的模糊聚类程序实现
模糊数学已经使用到各个领域,其在图像的分割中也是常用的经典方法,而且实时在其基础上能有些创新。本文通过两天来对模糊数学基础知识学习进行个小的poject巩固。本文标题兼主要内容为基于模糊等价关系的模糊聚类程序实现。
为什么要把模糊聚类分析基于模糊等价关系之上呢?模糊等价关系是同时满足自反性、对称性和传递性的模糊关系,因此必定有如下特性:
(1)自反性:保证关系中元素和元素本身是同一类
(2)对称性:保证元素A与B同类,则B与A也同类
(3)传递性:若A与B同类,B与C同类,则A与C同类
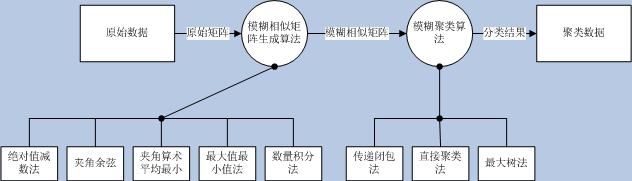
一般的聚类分析流程图如下
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:模糊聚类分析
clc
% 1)原始矩阵
disp('1)原始矩阵')
A = [5 5 3 2;
2 3 4 5;
5 5 2 3;
1 5 3 1;
2 4 5 1]
% 2)计算相似矩阵M
disp('2)计算相似矩阵M')
M = abs_sub(A, 5, 4)
% 3)计算模糊等价矩阵
disp('3)计算模糊等价矩阵')
N = matrix_com(M, 5)
% 4)λ聚类分析
r = 0.4;
sprintf('4)λ聚类分析(λ=%0.1f)', r)
Q = cluster(N, r)
Ø 下面分步骤实现每个过程中的调用函数
(1)获取原始矩阵
| 地方 |
空气 |
水 |
土壤 |
植被 |
| A |
5 |
5 |
3 |
2 |
| B |
2 |
3 |
4 |
5 |
| C |
5 |
5 |
2 |
3 |
| D |
1 |
5 |
3 |
1 |
| E |
2 |
4 |
5 |
1 |
由上表很容易一一对应获得矩阵
A = [5 5 3 2;
2 3 4 5;
5 5 2 3;
1 5 3 1;
2 4 5 1]
矩阵的行代表对象,矩阵的列代表对象具有的性质。
(2)计算相似矩阵
方法很多,这里使用很简单的绝对值减法,其数学公式如下
代表相似矩阵中的第i行第j列元素,代表A矩阵的第i行第j列元素。
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:绝对值减数法计算相对矩阵
function y = abs_sub(array, m, n);
% array - Input array original array
% m - number of objects
% n - number of properties
c = 0.1;
temp = 0;
for i = 1:m
for j = 1:m
for k = 1:n
temp = temp + abs(array(i,k)-array(j,k));
end
y(i,j) = 1 - c*temp;
temp = 0;
end
end
(3)计算模糊等价矩阵
这里利用离散数学里面的关系的合成运算方法,通过迭代计算等价矩阵。
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:模糊矩阵合成计算传递闭包
function y = matrix_com(array, m);
% array - Input array original array
% m - number of objects
% n - number of properties
flag = 0;%是否找到传递闭包的标志
temp = 0;
cnt = 0;
while ~flag
y = temp;
for i=1:m
for j=1:m
temp(i,j) = 0;
for k=1:m
if cnt==0
temp(i,j)=max(temp(i,j),min(array(i,k), array(k,j)));
else
temp(i,j)=max(temp(i,j),min(y(i,k), y(k,j)));
end
end
end
end
cnt = cnt + 1;
if y == temp
flag = 1;%传递闭包已找到
end
end
(4)截值聚类分析
很简单,比如有矩阵
A = [5 5 3 2;
2 3 4 5;
5 5 2 3;
1 5 3 1;
2 4 5 1]
使用截值r=3,则将A矩阵中比3小的值置0,大于等于3的值置1。结果为
A = [1 1 1 0;
0 1 1 1;
1 1 0 1;
0 1 1 0;
0 1 1 0]
使用简单的matlab程序实现如下
%作者:夏侯佐鑫
%日期:2012-07-15
%功能:λ聚类分析
function y = cluster(array, r);
% array -模糊相似矩阵或模糊等价矩阵
% r -聚类截距
if r>1 | r<0
error('第二个参数必须小于1');
end
len = length(array);
for i=1:len
for j=1:len
if array(i,j)>=r
y(i,j) = 1;
else
y(i,j) = 0;
end
end
end
Ø 最后通过matlab输出结果进一步认识整个模糊聚类的过程
1)原始矩阵
A =
5 5 3 2
2 3 4 5
5 5 2 3
1 5 3 1
2 4 5 1
2)计算相似矩阵M
M =
1 1/10 4/5 1/2 3/10
1/10 1 1/10 1/5 2/5
4/5 1/10 1 3/10 1/10
1/2 1/5 3/10 1 3/5
3/10 2/5 1/10 3/5 1
3)计算模糊等价矩阵
N =
1 2/5 4/5 1/2 1/2
2/5 1 2/5 2/5 2/5
4/5 2/5 1 1/2 1/2
1/2 2/5 1/2 1 3/5
1/2 2/5 1/2 3/5 1
4)λ聚类分析(λ=0.6)
Q =
1 0 1 0 0
0 1 0 0 0
1 0 1 0 0
0 0 0 1 1
0 0 0 1 1
所以,当r=0.6时,最终分类结果为{A,C},{D,E},{B,C}三组。选择不同的r值得到不同的分类结果。