- Python算法L5:贪心算法
小熊同学哦
Python算法算法python贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点:缺点:结语贪心算法(GreedyAlgorithm)是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是,在保证每一步局部最优的情况下,希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
- 非对称加密算法————RSA理论及详情
hu19930613
转自:https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前,所有的加密方法都是同一种模式:(1)甲方选择某一种加密规则,对信息进行加密;(2)乙方使用同一种规则,对信息进行解密。由于加密和解密使用同样规则(简称"密钥"),这被称为"对称加密算法"(Symmetric-keyalgorithm)。这种加密模式有一个最大弱点
- 数据结构 1
五花肉村长
数据结构算法开发语言c语言visualstudio
1.什么是数据结构数据结构(DataStructure)是计算机存储和组织数据的方式,是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法(Algorithm)就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识,可以去看《剑指offer》和《
- 三点or多点的变换矩阵求解opencv & eigen
合工大机器人实验室
C++矩阵opencv线性代数
《Estimating3-DRigidBodyTransformations:AComparisonofFourMajorAlgorithms》,它使用SVD方法计算T和t。只要算出变换矩阵,就可以算出A坐标系的一个点P在坐标系B里的对应点坐标,即R为3x3的转换矩阵,t为3x1的位移变换向量,这里点坐标均为3x1的列向量(非齐次形式,齐次形式下为4x1列向量,多出的一个元素值补1而已)。理论上只
- 详解贪心算法
凭君语未可
算法软考算法贪心算法
贪心算法什么是贪心算法?贪心算法的特点贪心算法的应用场景贪心算法的基本思路贪心算法的经典应用1.活动选择问题2.最小硬币找零问题3.霍夫曼编码问题贪心算法的正确性贪心算法的优缺点总结什么是贪心算法?贪心算法(GreedyAlgorithm)是一种基于每一步都选择当前最优解的算法设计思想。它在每个阶段总是做出在当前看来最优的选择(局部最优解),而不回溯或考虑整个问题的全局最优性。它期望通过这样逐步构
- 算法设计与分析 合并排序的递归实现算法
Jxcupupup
算法算法算法设计与分析
合并排序的递归实现算法。输入:先输入进行合并排序元素的个数,然后依次随机输入(或随机生成)每个数字。输出:元素排序后的结果,数字之间不加任何标识符。示//完整代码在GitHub上//https://github.com/Jxcup/Course_Algorithm_Analysis-Design/blob/main/MergeSort_iteration.cpp//合并排序递归#includeus
- c语言输入两个字符串 按字典数序比较大小,算法学习笔记(一)C++排序函数、映射技巧与字典树...
Nature自然科研
c语言输入两个字符串按字典数序比较大小
1.头文件algorithm中有函数sort()用于排序,参数为:排序起始地址,排序结束地址,排序规则(返回bool型)例如,要将array[]={5,7,1,2,9}升序排列,则使用:boolcmp(inta,intb);intmain(){intarray[]={5,7,1,2,9};sort(array,array+5,cmp);for(inti=0;icoutb)returnfalse;e
- 遗传算法(Genetic Algorithm,GA)-基于MATLAB环境实现
朱佩棋(代码版)
启发式算法启发式算法算法matlab
1.GA简介geneticalgorithm,美国Holland教授创立,基于达尔文进化论和孟德尔的遗传学说。遗传算法类比了生物界中自然选择、交叉、变异等自然进化方式,利用数码串类比染色体,通过选择、交叉、变异等遗传算子模拟生物的进化过程。1.1遗传算法的流程1.编码伪代码:2.产生初始群体Chooseinitialpopulation3.计算适应度Evaluatethefitnessofeach
- 【译】Swift算法俱乐部-布隆过滤器
Andy_Ron
Swift算法俱乐部本文是对SwiftAlgorithmClub翻译的一篇文章。SwiftAlgorithmClub是raywenderlich.com网站出品的用Swift实现算法和数据结构的开源项目,目前在GitHub上有18000+⭐️,我初略统计了一下,大概有一百左右个的算法和数据结构,基本上常见的都包含了,是iOSer学习算法和数据结构不错的资源。andyRon/swift-algori
- AdaBoost算法(AdbBoost Algorithm)—有监督学习方法、非概率模型、判别模型、非线性模型、非参数化模型、批量学习
剑海风云
ArtificialIntelligence人工智能机器学习提升方法AdaBoost
定义输入:训练数据集T={(x1,y1),(x2,y2),⋯ ,(xN,yN)}T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中,xi∈χ⊆Rn,yi∈y={−1,+1}x_i\in\chi\subseteqR^n,y_i\in{\tty}=\{-1,+1\}xi∈χ⊆Rn,yi∈y={−1,+1}
- Study Plan For Algorithms - Part29
五月的风与火
StudyPlanForAlgorithmspython算法数据结构
1.在排序数组中查找数字统计一个数字在排序数组中出现的次数。方法一:defsearch(nums,target):returnhelper(nums,target)-helper(nums,target-1)defhelper(nums,target):i=0j=len(nums)-1whileitargetor(lowerandnums[mid]>=target):right=mid-1else
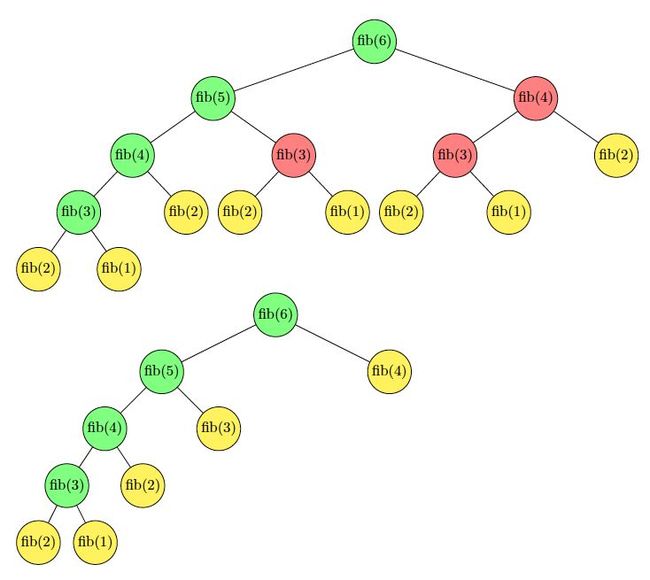
- 斐波纳契数列(f(n)=f(n-1)+f(n-2))问题
剑海风云
Algorithm算法数列
packageorg.nxt.algorithm.series;importjava.math.BigInteger;/***fibonacciseries*@authornanxiaotao**/publicclassFibonacciSeries{privatestaticBigInteger[][]matrix(BigInteger[][]arrLeft,BigInteger[][]arrR
- Kamada-Kawai 布局算法简介,nx.kamada_kawai_layout(G)
小桥流水---人工智能
人工智能深度学习机器学习算法算法python人工智能
nx.kamada_kawai_layout(G)是NetworkX中用于图布局的一个函数,它基于Kamada-Kawai弹簧嵌入算法(Kamada-KawaiSpringLayoutAlgorithm)。这是一个经典的力导向布局算法,它特别适用于中小型图的可视化,能够让节点的位置更直观地反映它们之间的关系。Kamada-Kawai布局算法简介Kamada-Kawai算法是一种用于图的二维或三维可
- 翻译 Compaction wiki
i_need_job
网址:https://github.com/facebook/rocksdb/wiki/Compaction有道CompactionCompactionalgorithmsconstraintheLSMtreeshape.Theydeterminewhichsortedrunscanbemergedbyitandwhichsortedrunsneedtobeaccessedforareadoper
- Go-Snowflake 项目教程
喻季福
Go-Snowflake项目教程go-snowflake❄AnLockFreeIDGeneratorforGolangbasedonSnowflakeAlgorithm(Twitterannounced).项目地址:https://gitcode.com/gh_mirrors/go/go-snowflake项目介绍Go-Snowflake是一个基于Go语言实现的分布式唯一ID生成器,灵感来源于Tw
- 2023ICPC济南站训练补题
farawaytravelerchy
ACM-ICPC训练补题算法python
title:2023ICPC济南站VP补题记录(第48届)date:2024-01-1812:16:23mathjax:truetags:XCPCcategories:Algorithm文章目录2023ICPC济南站训练补题注:暂时更新vp时ac的4道题,其余题目之后持续更新[Problem-D-LargestDigit](https://codeforces.com/gym/104901/pro
- 【算法】浅析贪心算法
Ustinian_310
算法贪心算法python
贪心算法:高效解决问题的策略1.引言在计算机科学和优化领域,贪心算法是一种常用的解决问题的策略。它以当前情况为基础,做出最优选择,从而希望最终结果也是最优的。本文将带你了解贪心算法的原理、使用方法及其在实际应用中的意义,并通过代码示例和图示帮助大家更好地理解。2.贪心算法简介2.1定义贪心算法(GreedyAlgorithm)是一种在每一步选择中都采取当前状态下最优(即最有利)的选择,从而希望导致
- OpenCV结构分析与形状描述符(8)点集凸包计算函数convexHull()的使用
jndingxin
OpenCVopencv人工智能计算机视觉
操作系统:ubuntu22.04OpenCV版本:OpenCV4.9IDE:VisualStudioCode编程语言:C++11算法描述查找一个点集的凸包。函数cv::convexHull使用斯克拉斯基算法(Sklansky’salgorithm)来查找一个二维点集的凸包,在当前实现中该算法的时间复杂度为O(NlogN)。函数cv::convexHull是OpenCV库中的一个功能,用于计算一组二
- Java算法之判断平衡二叉树
持续输出...
#Java算法算法
判断一棵二叉树是否是平衡二叉树(即AVL树)是一个常见的问题。平衡二叉树的定义是:对于树中的每个节点,其左右子树的高度差不超过1。我们可以通过递归的方法来判断一棵二叉树是否是平衡的packagecom.huawei.od.huawei.algorithm;/***@ClassName:IsBalancedBinaryTree是否是平衡二叉树*@Desc:判断一棵二叉树是否是平衡二叉树(即AVL树)
- Python深度学习-环境
cunzai1985
tensorflowpython深度学习人工智能anaconda
Python深度学习-环境(PythonDeepLearning-Environment)Inthischapter,wewilllearnabouttheenvironmentsetupforPythonDeepLearning.Wehavetoinstallthefollowingsoftwareformakingdeeplearningalgorithms.在本章中,我们将学习为Python
- 探索图形算法的奇妙世界:goraph
孔岱怀
探索图形算法的奇妙世界:goraphgoraphPackagegoraphimplementsgraphdatastructureandalgorithms.项目地址:https://gitcode.com/gh_mirrors/go/goraph在编程领域,数据结构和算法是构建高效应用的基础。今天,我们要向您推荐一款名为【goraph】的开源项目,它是一个用Go语言实现的图形数据结构及其算法库。
- 【小白深度教程 1.5】手把手教你用立体匹配进行双目深度估计,以及 3D 点云生成(含 Python 代码解读)
小寒学姐学AI
从零开始的深度补全和深度估计3dpython人工智能计算机视觉自动驾驶深度学习笔记
【小白深度教程1.5】手把手教你用立体匹配进行双目深度估计,以及3D点云生成(含Python代码解读)1.立体匹配的原理2.块匹配算法(BlockMatchingAlgorithm)2.1代码中的立体匹配过程概述2.2代码原理及公式2.2.1.窗口匹配和代价函数(SAD)2.2.2.匹配过程2.2.3.视差图生成2.3代码的整体算法流程2.4性能与优化3.加载双目图像计算视差4.读取相机参数并计算
- 关于多变量超扭曲算法的到达时间评估
beegreen
控制与信号处理算法动态规划数学建模
关于多变量超扭曲算法的到达时间评估I.引言II.问题陈述III.李雅普诺夫函数的性质IV.到达时间估计V.原始系统的到达时间估计VI.最差干扰VII.数值问题和示例A.示例VIII.结论致谢参考文献REFERENCESOnMultivariableSuper-TwistingAlgorithmReachingTimeAssessment摘要——本文提供了一种基于线性矩阵不等式(LMI)的程序,用于
- SSH Secure File Transfer Client连接远程设备报“algorithm negotiation failed”错的解决方法
成长Bar
uinx/linuxnegotiationfailedalgorithmnegotiatio
SSHSecureFileTransferClient连接远程设备报“algorithmnegotiationfailed”错的解决方法sshclient报algorithmnegotiationfailed的解决方法之一是修改sshd的配置文件,请参考以下三个步骤进行解决该问题。第一步:进入配置文件/etc/ssh/sshd_config第二步:在配置文件中添加Ciphersaes128-cbc
- 机器学习系列12:反向传播算法
SuperFengCode
机器学习系列机器学习神经网络反向传播算法梯度检验机器学习笔记
当我们要运用高级算法进行梯度下降时,需要计算两个值,代价函数和代价函数的偏导数:代价函数我们之前已经知道怎么求了,现在只需要求代价函数的偏导数即可。采用如下方法,先进行前向传播算法,然后再进行反向传播算法(BackpropagationAlgorithm),反向传播算法与前向传播算法方向相反,它用来求代价函数的偏导数。具体过程看下图:用δ作为误差,计算方法为:有时我们在运用反向传播算法时会遇到bu
- [Algorithm][综合训练][栈和排序][加减]详细讲解
DieSnowK
[OJ]#[综合训练]Algorithm算法综合训练栈和排序加减C++详细讲解
目录1.栈和排序1.题目链接2.算法原理详解&&代码实现2.加减1.题目链接2.算法原理详解&&代码实现1.栈和排序1.题目链接栈和排序2.算法原理详解&&代码实现解法:栈+贪心->每次尽可能先让当前需要的最大值弹出去vectorsolve(vector&a){intn=a.size();vectorhash(n+1,false);vectorret;intaim=n;stackst;for(au
- What are some of halcon‘s best algorithms that opencv doesn‘t implement
0010000100
OpenCVopencv人工智能
HALCON,ahighlyoptimizedmachinevisionlibrary,offersarangeofadvancedalgorithmsthatOpenCVeitherdoesn’timplementorhandlesdifferently.SomeofthekeystrengthsofHALCONcomparedtoOpenCVinclude:Shape-BasedMatchin
- [ A*实现 ] C++,矩阵地图
Arik (IoT)
移动机器人路径规划路径规划
参考文献:A*寻路算法C++简单实现(csdn.net)ROSpackageofAstaralgorithm(github.com)实现代码:https://gitee.com/upcgyl/astar.git存在问题:地图目前必须是可搜索到路径周围点寻找太过复杂OpenList和CloseList结构不统一导致查找函数需要写两个后续优化:思考二叉堆的实现方式优化地图输入区分linux端:增加Op
- [C++] C++11详解 (四)lambda表达式
水墨不写bug
Cppc++开发语言
标题:[C++]C++11详解(四)lambda表达式@水墨不写bug目录一、lambda表达式lambda表达式语法lambda表达式与仿函数关系正文开始:一、lambda表达式作为C++学习者,你一定对algorithm中的sort函数十分熟悉,sort函数默认可以对自定义类型的数据按照升序排序。在实际生活中,我们常常遇到的场景是需要对自定义类型对象排序。如何对自定义类型排序?其实就是按照某一
- 令牌桶算法:原理与代码实现
Lill_bin
杂谈网络服务器运维大数据java开发语言后端
引言令牌桶算法(TokenBucketAlgorithm)是一种网络流量整形(TrafficShaping)和速率限制(RateLimiting)的算法。它能够限制数据传输的平均速率,同时允许某种程度的突发传输。在许多场景中,如网络带宽管理、API速率限制等,令牌桶算法都得到了广泛的应用。原理令牌桶算法的核心思想是使用一个虚拟的“桶”来存储令牌,每个令牌代表一个数据包的传输权限。系统按照固定的速率
- 安装数据库首次应用
Array_06
javaoraclesql
可是为什么再一次失败之后就变成直接跳过那个要求
enter full pathname of java.exe的界面
这个java.exe是你的Oracle 11g安装目录中例如:【F:\app\chen\product\11.2.0\dbhome_1\jdk\jre\bin】下的java.exe 。不是你的电脑安装的java jdk下的java.exe!
注意第一次,使用SQL D
- Weblogic Server Console密码修改和遗忘解决方法
bijian1013
Welogic
在工作中一同事将Weblogic的console的密码忘记了,通过网上查询资料解决,实践整理了一下。
一.修改Console密码
打开weblogic控制台,安全领域 --> myrealm -->&n
- IllegalStateException: Cannot forward a response that is already committed
Cwind
javaServlets
对于初学者来说,一个常见的误解是:当调用 forward() 或者 sendRedirect() 时控制流将会自动跳出原函数。标题所示错误通常是基于此误解而引起的。 示例代码:
protected void doPost() {
if (someCondition) {
sendRedirect();
}
forward(); // Thi
- 基于流的装饰设计模式
木zi_鸣
设计模式
当想要对已有类的对象进行功能增强时,可以定义一个类,将已有对象传入,基于已有的功能,并提供加强功能。
自定义的类成为装饰类
模仿BufferedReader,对Reader进行包装,体现装饰设计模式
装饰类通常会通过构造方法接受被装饰的对象,并基于被装饰的对象功能,提供更强的功能。
装饰模式比继承灵活,避免继承臃肿,降低了类与类之间的关系
装饰类因为增强已有对象,具备的功能该
- Linux中的uniq命令
被触发
linux
Linux命令uniq的作用是过滤重复部分显示文件内容,这个命令读取输入文件,并比较相邻的行。在正常情 况下,第二个及以后更多个重复行将被删去,行比较是根据所用字符集的排序序列进行的。该命令加工后的结果写到输出文件中。输入文件和输出文件必须不同。如 果输入文件用“- ”表示,则从标准输入读取。
AD:
uniq [选项] 文件
说明:这个命令读取输入文件,并比较相邻的行。在正常情况下,第二个
- 正则表达式Pattern
肆无忌惮_
Pattern
正则表达式是符合一定规则的表达式,用来专门操作字符串,对字符创进行匹配,切割,替换,获取。
例如,我们需要对QQ号码格式进行检验
规则是长度6~12位 不能0开头 只能是数字,我们可以一位一位进行比较,利用parseLong进行判断,或者是用正则表达式来匹配[1-9][0-9]{4,14} 或者 [1-9]\d{4,14}
&nbs
- Oracle高级查询之OVER (PARTITION BY ..)
知了ing
oraclesql
一、rank()/dense_rank() over(partition by ...order by ...)
现在客户有这样一个需求,查询每个部门工资最高的雇员的信息,相信有一定oracle应用知识的同学都能写出下面的SQL语句:
select e.ename, e.job, e.sal, e.deptno
from scott.emp e,
(se
- Python调试
矮蛋蛋
pythonpdb
原文地址:
http://blog.csdn.net/xuyuefei1988/article/details/19399137
1、下面网上收罗的资料初学者应该够用了,但对比IBM的Python 代码调试技巧:
IBM:包括 pdb 模块、利用 PyDev 和 Eclipse 集成进行调试、PyCharm 以及 Debug 日志进行调试:
http://www.ibm.com/d
- webservice传递自定义对象时函数为空,以及boolean不对应的问题
alleni123
webservice
今天在客户端调用方法
NodeStatus status=iservice.getNodeStatus().
结果NodeStatus的属性都是null。
进行debug之后,发现服务器端返回的确实是有值的对象。
后来发现原来是因为在客户端,NodeStatus的setter全部被我删除了。
本来是因为逻辑上不需要在客户端使用setter, 结果改了之后竟然不能获取带属性值的
- java如何干掉指针,又如何巧妙的通过引用来操作指针————>说的就是java指针
百合不是茶
C语言的强大在于可以直接操作指针的地址,通过改变指针的地址指向来达到更改地址的目的,又是由于c语言的指针过于强大,初学者很难掌握, java的出现解决了c,c++中指针的问题 java将指针封装在底层,开发人员是不能够去操作指针的地址,但是可以通过引用来间接的操作:
定义一个指针p来指向a的地址(&是地址符号):
- Eclipse打不开,提示“An error has occurred.See the log file ***/.log”
bijian1013
eclipse
打开eclipse工作目录的\.metadata\.log文件,发现如下错误:
!ENTRY org.eclipse.osgi 4 0 2012-09-10 09:28:57.139
!MESSAGE Application error
!STACK 1
java.lang.NoClassDefFoundError: org/eclipse/core/resources/IContai
- spring aop实例annotation方法实现
bijian1013
javaspringAOPannotation
在spring aop实例中我们通过配置xml文件来实现AOP,这里学习使用annotation来实现,使用annotation其实就是指明具体的aspect,pointcut和advice。1.申明一个切面(用一个类来实现)在这个切面里,包括了advice和pointcut
AdviceMethods.jav
- [Velocity一]Velocity语法基础入门
bit1129
velocity
用户和开发人员参考文档
http://velocity.apache.org/engine/releases/velocity-1.7/developer-guide.html
注释
1.行级注释##
2.多行注释#* *#
变量定义
使用$开头的字符串是变量定义,例如$var1, $var2,
赋值
使用#set为变量赋值,例
- 【Kafka十一】关于Kafka的副本管理
bit1129
kafka
1. 关于request.required.acks
request.required.acks控制者Producer写请求的什么时候可以确认写成功,默认是0,
0表示即不进行确认即返回。
1表示Leader写成功即返回,此时还没有进行写数据同步到其它Follower Partition中
-1表示根据指定的最少Partition确认后才返回,这个在
Th
- lua统计nginx内部变量数据
ronin47
lua nginx 统计
server {
listen 80;
server_name photo.domain.com;
location /{set $str $uri;
content_by_lua '
local url = ngx.var.uri
local res = ngx.location.capture(
- java-11.二叉树中节点的最大距离
bylijinnan
java
import java.util.ArrayList;
import java.util.List;
public class MaxLenInBinTree {
/*
a. 1
/ \
2 3
/ \ / \
4 5 6 7
max=4 pass "root"
- Netty源码学习-ReadTimeoutHandler
bylijinnan
javanetty
ReadTimeoutHandler的实现思路:
开启一个定时任务,如果在指定时间内没有接收到消息,则抛出ReadTimeoutException
这个异常的捕获,在开发中,交给跟在ReadTimeoutHandler后面的ChannelHandler,例如
private final ChannelHandler timeoutHandler =
new ReadTim
- jquery验证上传文件样式及大小(好用)
cngolon
文件上传jquery验证
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
<script src="jquery1.8/jquery-1.8.0.
- 浏览器兼容【转】
cuishikuan
css浏览器IE
浏览器兼容问题一:不同浏览器的标签默认的外补丁和内补丁不同
问题症状:随便写几个标签,不加样式控制的情况下,各自的margin 和padding差异较大。
碰到频率:100%
解决方案:CSS里 *{margin:0;padding:0;}
备注:这个是最常见的也是最易解决的一个浏览器兼容性问题,几乎所有的CSS文件开头都会用通配符*来设
- Shell特殊变量:Shell $0, $#, $*, $@, $?, $$和命令行参数
daizj
shell$#$?特殊变量
前面已经讲到,变量名只能包含数字、字母和下划线,因为某些包含其他字符的变量有特殊含义,这样的变量被称为特殊变量。例如,$ 表示当前Shell进程的ID,即pid,看下面的代码:
$echo $$
运行结果
29949
特殊变量列表 变量 含义 $0 当前脚本的文件名 $n 传递给脚本或函数的参数。n 是一个数字,表示第几个参数。例如,第一个
- 程序设计KISS 原则-------KEEP IT SIMPLE, STUPID!
dcj3sjt126com
unix
翻到一本书,讲到编程一般原则是kiss:Keep It Simple, Stupid.对这个原则深有体会,其实不仅编程如此,而且系统架构也是如此。
KEEP IT SIMPLE, STUPID! 编写只做一件事情,并且要做好的程序;编写可以在一起工作的程序,编写处理文本流的程序,因为这是通用的接口。这就是UNIX哲学.所有的哲学真 正的浓缩为一个铁一样的定律,高明的工程师的神圣的“KISS 原
- android Activity间List传值
dcj3sjt126com
Activity
第一个Activity:
import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Map;import android.app.Activity;import android.content.Intent;import android.os.Bundle;import a
- tomcat 设置java虚拟机内存
eksliang
tomcat 内存设置
转载请出自出处:http://eksliang.iteye.com/blog/2117772
http://eksliang.iteye.com/
常见的内存溢出有以下两种:
java.lang.OutOfMemoryError: PermGen space
java.lang.OutOfMemoryError: Java heap space
------------
- Android 数据库事务处理
gqdy365
android
使用SQLiteDatabase的beginTransaction()方法可以开启一个事务,程序执行到endTransaction() 方法时会检查事务的标志是否为成功,如果程序执行到endTransaction()之前调用了setTransactionSuccessful() 方法设置事务的标志为成功则提交事务,如果没有调用setTransactionSuccessful() 方法则回滚事务。事
- Java 打开浏览器
hw1287789687
打开网址open浏览器open browser打开url打开浏览器
使用java 语言如何打开浏览器呢?
我们先研究下在cmd窗口中,如何打开网址
使用IE 打开
D:\software\bin>cmd /c start iexplore http://hw1287789687.iteye.com/blog/2153709
使用火狐打开
D:\software\bin>cmd /c start firefox http://hw1287789
- ReplaceGoogleCDN:将 Google CDN 替换为国内的 Chrome 插件
justjavac
chromeGooglegoogle apichrome插件
Chrome Web Store 安装地址: https://chrome.google.com/webstore/detail/replace-google-cdn/kpampjmfiopfpkkepbllemkibefkiice
由于众所周知的原因,只需替换一个域名就可以继续使用Google提供的前端公共库了。 同样,通过script标记引用这些资源,让网站访问速度瞬间提速吧
- 进程VS.线程
m635674608
线程
资料来源:
http://www.liaoxuefeng.com/wiki/001374738125095c955c1e6d8bb493182103fac9270762a000/001397567993007df355a3394da48f0bf14960f0c78753f000 1、Apache最早就是采用多进程模式 2、IIS服务器默认采用多线程模式 3、多进程优缺点 优点:
多进程模式最大
- Linux下安装MemCached
字符串
memcached
前提准备:1. MemCached目前最新版本为:1.4.22,可以从官网下载到。2. MemCached依赖libevent,因此在安装MemCached之前需要先安装libevent。2.1 运行下面命令,查看系统是否已安装libevent。[root@SecurityCheck ~]# rpm -qa|grep libevent libevent-headers-1.4.13-4.el6.n
- java设计模式之--jdk动态代理(实现aop编程)
Supanccy2013
javaDAO设计模式AOP
与静态代理类对照的是动态代理类,动态代理类的字节码在程序运行时由Java反射机制动态生成,无需程序员手工编写它的源代码。动态代理类不仅简化了编程工作,而且提高了软件系统的可扩展性,因为Java 反射机制可以生成任意类型的动态代理类。java.lang.reflect 包中的Proxy类和InvocationHandler 接口提供了生成动态代理类的能力。
&
- Spring 4.2新特性-对java8默认方法(default method)定义Bean的支持
wiselyman
spring 4
2.1 默认方法(default method)
java8引入了一个default medthod;
用来扩展已有的接口,在对已有接口的使用不产生任何影响的情况下,添加扩展
使用default关键字
Spring 4.2支持加载在默认方法里声明的bean
2.2
将要被声明成bean的类
public class DemoService {