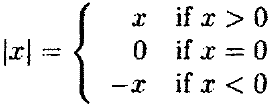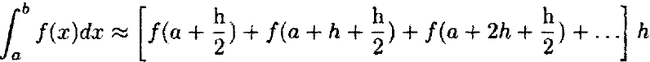Lisp-Stat 翻译 —— 第三章 Lisp编程
第三章 Lisp编程
上一章我们使用了一些内建的Lisp函数和Lisp-Stat函数来运行一些有趣的运算。我们构建的表达式中的一些还是相当复杂的。当你发觉自己多次键入相同的表达式的时候(当然你使用的数据可能略微有些不同),你自然就想为这个表达式引入一些速记符,也就是说你想要定义自己的函数了。函数定义是Lisp编程的基础操作。第2.7节已经对这个主题给出了一个简单的介绍,现在是深入探索的时候了。在对如何定义一个Lisp函数进行一个简略的复习之后,我们将检验一些需要的技术以开发功能更强大的函数:状态求值、递归和迭代、局部变量、函数式数据、映射和赋值。
除了介绍定义函数的工具,本章也展示了一些Lisp编程常用编程技术和原则。尤其地,对于本章的大多数情况我都会使用函数式风格直至本章结束,目的是避免使用赋值方式改变变量的值(注:这里提到的原则也是函数式的目的之一,即函数可以使用外部变量,但在函数的整个执行过程中不对变量进行写操作,不破坏外部变量,这样的函数要非破坏性函数,反之叫破坏性函数,在《Practical Common Lisp》和《On Lisp》里你将接触大量的非破坏性函数和他们的破坏性版本,都有其各自的书写约定)。本章的开发严重依赖Abelson和Sussman的《Scheme:计算机程序结构与解释》的前两章。为了允许我们集中精力到编程过程本身,本章只使用我们见过的基本类型数据:数值型、字符串型和列表型。Lisp和Lisp-Stat提供了若干额外的数据类型和用来操作这些数据类型的函数,这些可以在自定义函数里当做组件。下一章我将介绍一些这样的函数。
3.1 编写简单的函数
Lisp函数需要使用特殊形式defun来定义。defun的基础语法是(defun <name> <parameters> <body>),这里的<name>是用来引用该函数的符号(即函数名),<parameters>是用来命名函数形参的符号列表,<body>即由一个或多个表达式组成。当调用函数的时候,<body>里的表达式将按次序求值,最后一个表达式的求值结果将作为函数的返回值。当前我们不会使用函数体里超过一个表达式的函数。defun的参数都不需要使用引号,因为defun不对参数求值。
举个例子,这里有个函数,功能是计算一个数据集的平方和,我们可以对一个数值列表使用这个函数,就像第二章里使用的那些函数一样:
> (defun sum-of-squares (x)
(sum (* x x)))
SUM-OF-SQUARES
> (sum-of-squares (list 1 2 3))
14 该定义使用了Lisp-Stat提供的矢量运算机制。函数sum将计算参数的每一个项的和。
也可以定义一个带多个参数的函数,例如,计算内积的函数可以定义成这样:
> (defun my-inner-product (x y) (sum (* x y))) MY-INNER-PRODUCT我将将用my-inner-product函数,而不调用inner-product函数,目的就是不失去Lisp-Stat内部对inner-product函数的定义,Lisp-Stat对函数的定义比我们定义的函数更缜密一些。
使用defun定义的函数也可以用来定义其它函数,例如,使用sum-of-squares函数,我们可以定义一个计算两个数据列表欧几里德距离的函数:
> (defun distance (x y)
(sqrt (sum-of-squres (- x y))))
DISTANCE 使用defun,我们可以开发函数作为复杂表达式的速记符号。然而,我们仍然被局限在我们能使用的表达式的能力里。假设我们想要将以下给定的绝对值表达式的定义转换为Lisp表达式。
为了编写这个函数,我们需要一些谓词来比较数字和0,还需要一个条件求值结构来对不同的表达式求值,这些表达式是根据谓词范围的结果得到的。
3.2 谓词和逻辑表达式
谓词就是函数用来确定一个条件是真是假的词项,谓词对假条件返回nil,有时也返回non-nil,对于真条件,一般返回t。为了比较数值,我们可以使用谓词'<'、'>'、'='和其它比较谓词。这些谓词都要带两个货更多参数。谓词'<'的参数以升序排列,则返回真:
> (< 1 2) T > (< 2 1) NIL > (< 1 2 3) T > (< 1 3 2) NIL谓词'>'与'<'相似。谓词'='当所有参数都相等时返回真:
> (= 1 2) NIL > (= 1 1) T > (= 1 1 1) T在Lisp-Stat里 比较谓词是矢量化的。'>'和'<'谓词的非组合参数必须是实数;对于'='谓词的其非组合参数必须是实数或者复数,其它类型的值,都会引发错误。
使用特殊形式and和or,还有函数not,可以在这些简单的谓词基础上构建更复杂的谓词。例如,我们可以定义一个函数来测试一个数字是否在区间(3, 5]内:
> (defun in-range (x)
(and (< 3 x) (<= x 5)))
IN-RANGE 特殊形式and带两个或更多参数,然后每次对一个参数求值,直到所有参数都求值过并返回真,或者其中一个为假。一旦某一个参数为假,就不需要对其它参数进行求值了。
为了测试一个参数是否不再区间(3, 5]内,我们可以使用特殊形式or:
> (defun not-in-range (x) (or (>= 3 x) (> x 5))) NOT-IN-RANGE与and相似,特殊形式or也带两个或更多参数,or每次对一个参数求值,直到一个参数为真,或者所有参数都为假是停止求值。
定义not-in-range的另一种方式是使用in-range函数与not函数的联合:
> (defun not-in-range (x) (or (>= 3 x) (> x 5))) NOT-IN-RANGE练习 3.1
略。
3.3 条件求值
最基本的Lisp条件求值结构是cond。使用cond和比较谓词刚才已经介绍过了,我们可以定义一个函数来计算一个数值的绝对值:
> (defun my-abs (x)
(cond ((> x 0) x)
((= x 0) 0)
((< x 0) (- x))))
MY-ABS 条件表达式的一般形式如下:
(cond (<p 1> <e 1>)
(<p 2> <e 2>)
...
(<p n> <e n>))
类似列表(<p 1> <e 1>)的形式叫做条件语句。每个条件语句的第一个表达式,比如<p 1>,... ,<p n>是谓词表达式,当真的时候求值为非nil,当假的时候求值为nil。cond一次只运行一条语句,它求值表达式直到一个表达式为真。如果其中的一个谓词为真,比如说就是<p i>,那么它对应的序列表达式<e i>将被求值,它的结果作为cond表达式的结果。如果没有一个谓词为真,则返回nil。
在my-abs函数的定义里,我为3个条件语句使用了完整的谓词表达式。因为最后一个条件语句是一个默认值,我可以使用符号t作为谓词表达式。my-abs函数应该看起来是这样的:
> (defun my-abs (x)
(cond ((> x 0) x)
((= x 0) 0)
(t (-x)))) MY-ABS 因为最后一条语句的谓词总为真,所以上边的语句没有使用就用这条语句。
条件语句可能有好几条结果表达式,这些表达式按顺序执行,最终的求值结果将被返回。最终的那个表达式之前的表达式只对它们产生的副作用是有用的。例如,我们可以使用print函数和terpri函数来修改my-abs函数的定义,这样可以打印一条消息以指示哪条条件语句被使用了。print函数发送一个西航给解释器,该消息后紧跟一个它自身参数表达式的打印体和一个空格;terpri函数向解释器发送一个新行。新的定义如下:
> (defun my-abs (x)
(cond ((> x 0) (print 'first-clause) (terpri) x)
((= x 0) (print 'second-clause) (terpri) 0)
((< x 0) (print 'third-clause) (terpri) (-x))))
MY-ABS 当使用函数的时候,将提供一些关于求值过程的信息。
> (my-abs 3) FIRST-CLAUSE 3 > (my-abs -3) THIRD-CLAUSE 3
print函数的使用在这个特殊的例子里当然是愚蠢的,但是在一些复杂的函数里它可能会成为一个很有用的调试工具。
除了cond,Lisp还提供了一些其它的条件计算结构。它们中最重要的就是if。特殊形式if带3个表达式,一个谓词表达式,一个结果项,一个替代项。首先计算谓词表达式,如果为真,那么对结果项求值,结果项返回值作为if的返回值;否则,对替代表达式求值,并返回它的结果,如果没有提供这个可选的替代表达式,默认返回nil。使用if我们可以这么定义my-abs函数:
> (defun my-abs (x)
(if (> x 0)
x
(- x)))
MY-ABS if表达式的一般形式与cond表达式是等价的。
练习 3.2
略。
3.4 迭代和递归
Lisp是一种递归语言,其结果,在这一点上我们已经有足够的工具编写函数来践行数值计算,这些数值计算在其它语言里是需要特殊的迭代结构的。Lisp确实已经提供了一些迭代工具,下面我们就会看到一些,但是首先检测在仅仅使用递归的情况下能在多大程度上完成任务这点上是很有用的。
举个例子,让我们看一个计算数字x的平方根的算法。这个算法以对√x的起始猜测值y开始,然后像下式一样计算一个持续改进的猜测值:
这个过程将重复进行,直到当前参测值的平方与x足够接近为止。例如,对于√3,其起始猜测值为1,我们将进行以下步骤:
该算法可以追溯到公元一世界,是牛顿法解方程根的一个特例。我们可以使用Lisp来表示这个算法,通过定义一个函数sqrt-iter,它带一个初始猜测值和数值x,然后计算近似平方根值:
> (defun sqrt-iter (guess x)
(if (good-enough-p guess x)
guess
(sqrt-iter (improve guess x) x)))
SQRT-ITER 如果当前猜测值是一个满意值,返回它。否则,计算过程将使用一个改进的猜测值重复运行。
这个函数需要两个额外的函数,计算新猜测值的improve函数,还有测试当前值是否足够接近的good-enough-p函数。改进的函数可以简单地对上边给出的步骤编码,并定义为下边的样子:
> (defun improve (guess x)
(mean (list guess (/ x guess))))
IMPROVE 收敛测试需要一个收敛准则的选择和一个临界值,简单定义如下:
> (defun good-enough-p (guess x)
(< (abs (- (* guess guess) x)) 0.001))
GOOD-ENOUGH-P 将0.001作为临界值的选择当然是随意的。
使用sqrt-iter,我们可以定义一个平方根函数:
> (defun my-sqrt (x)
(sqrt-iter 1 x))
MY-SQRT 测试一下:
> (my-sqrt 9) 3.00009155413138函数sqrt-iter的定义是递归的,也就是说,它使用自己本身定义自己。但是由该函数产生的计算过程,与接下来的计算一个正整数的factorial数列的递归函数产生的过程是有些不同的:
> (defun factorial (n)
(if (= n 1)
1
(* n (factorial (- n 1)))))
FACTORIAL 这里factorial函数的值,当n为1的时候是1;当n>1时,按n(n-1)!计算。当这个factorial函数使用一个参数的时候,它建立一系列的递延操作直到它最后达到那个基础条件(本例就是n=1)为止,然后计算它们之间的相乘。为了持续跟踪这些递延的计算,需要的存储空间容量与计算过程中的步骤数量是呈现线性关系的。这样的计算过程叫线性递归。
与之相反,sqrt-iter函数产生的计算过程不需要持续追踪任何递延计算。所有的过程的状态信息都包含在一个单独的状态变量里,即当前的猜测值这一变量。可以用确定数目的状态变量来描述的计算过程叫做可迭代过程。
定义factorial函数的一个可迭代版本也是可能的。为了达到这一目的,我们能使用一个counter变量和一个product变量作为状态变量。每一步骤product变量都会与counter变量相乘,counter变量递增,直到counter变量大于n为止:
> (defun fact-iter (product counter n)
(if (> counter n)
product
(fact-iter (* counter product) (+ counter 1) n)))
FACT-ITER 现在我们能使用fact-iter函数,其参数pruduct和counter都为1,来定义factorial函数:
> (defun factorial (n)
(fact-iter 1 1 n))
FACTORIAL sqrt-iter和fact-iter这两个辅助函数在结构上很相似。因为定义一个能够产生迭代运算过程的函数,通常需要定义一个带这种结构的辅助函数,Lisp提供了一个可以简化这个过程的
特殊形式,同时避免一定要为这个辅助函数想一个名字。这个
特殊形式就是do。一个do表达式语法的简化版本如下:
(do ((<name 1> <initial 1> <update 1>)
...
(<name n> <initial n> <update n>))
(<test> <result>))
有两个参数:一个三元列表,后边还跟着一个列表,这个列表由一个终止测试表达式和一个结果表达式组成。三元表达式的每一项都由三部分组成,一个状态变量名,一个初始化表达式和一个更新表达式。do从对一个初始表达式求值开始,然后将表达式的值与状态变量绑定;接下来使用迭代变量对终止表达式求值,如果终止表达式的结果为真,结果对表达式求值并作为结果返回,否则,计算更新表达式,变量将与其新值绑定,计算终止测试,等等。
使用do我们可以如此编写my-sqrt函数:
> (defun my-sqrt (x)
(do ((guess 1 (improve guess x)))
((good-enough-p guess x) guess)))
MY-SQRT 如此,factorial函数变成:
> (defun factorial (n)
(do ((counter 1 (+ 1 counter))
(product 1 (* counter product)))
((> counter n) product)))
FACTORIAL 将这里的定义与sqrt-iter和fact-iter函数的原始定义进行比较,表明原始定义的每一块代码都将一个槽放进了do的结构里。对函数fact-iter初始化调用的参数表达式变成了初始化表达式,递归调用fact-iter函数时的参数表达式变成了更新表达式,函数fact-iter里的if表达式的test变成了do表达式的test表达式,if里的结果表达式变成了do的结果表达式。
do结构是非常强大的,但是它也是有一点恐怖的。对于使用sqrt-iter或者fact-iter函数的辅助函数来说,do可以很容易地想出一个简单的替代函数。重要的一点是,这里的初始化表达式和更新表达式是并行计算的,不是串行的。结果,三元结构元素的顺序如何指定是没有关系的。这与给一个没有调用的辅助函数传递参数的方式是类似的,函数调用之前,它的参数顺序是无所谓的。
练习 3.3
略。
练习 3.4
略。
3.5 环境
使用def和defun定义的变量和函数是全局变量和全局函数,一旦有变量或函数被定义,它们将持续存在直到它们被重新定义、取消定义,或者你结束了与解释器的会话。我们已经见过变量其它类型了:一个函数的参数在函数体里被用作局部变量。Lisp提供了一些其它的方法来构造局部变量,也允许你构造自己的局部函数。为了能够有效地使用这些方法,我们需要介绍一些新的想法和术语。
3.5.1 一些术语
让我们从一个很简单的例子开始。假设我们有一个全局变量是这么定义的:
> (def x 1) X然后再定义一个f函数:
> (defun f (x)
(+ x 1))
F 当我们使用一个参数的时候,比如是2,当f被调用的时候,f函数体里的变量x将引用这个参数:
> (f 2) 3一个变量和一个值得配对叫做绑定。在这个例子里,变量x与数值1有一个全局的绑定。当使用参数2调用函数的时候,创建了x的局部绑定,函数体将使用该局部绑定进行求值,这个局部绑定将屏蔽全局绑定。在特定时间绑定有效的那个变量集合叫做环境。一个特定绑定应用的表达式集合叫做这个绑定的作用域。在这个例子里,f函数体在这样的环境里求值,该环境由x与参数值的局部绑定组成,这个局部绑定的作用域是f的函数体。
下载,让我们做一点儿改变。定义另一个全局变量a:
> (def a 10)然后重定义函数f:
> (defun f (x) (+ x a))f的函数体现在引用了两个变量,x和a。变量x与函数的参数绑定,因此叫绑定变量。变量a没有与任何参数绑定,因此叫自由变量,函数f使用参数2时的会发生什么,该预测不会太难。
> (f 2) 12自由变量a的值可以来自全局环境或者null环境。
但是假设函数f从函数内部调用,例如,定义函数g:
> (defun g (a) (f 2))表达式(g 20)的值是多少呢?为了回答这个问题,我们需要知道Lisp用来确定自由变量的值的规则。这里有几种情况。一个就是在函数被调用的环境里查找自由变量的值,这个规则叫动态作用域。在我们的例子里,当f被调用时,变量a和数值20进行了绑定,表达式(g 20)的结果将是22。另一个方法是在函数原始定义里查找自由变量的值,这个叫静态作用域和词法作用域。因为函数f是在局部环境里定义的,该方法将在局部环境里查找a的值,在那里a是与10绑定的,表达式(g 20)的返回值是12。
Common Lisp使用静态作用域规则,所以:
> (g 20) 12当一个Common Lisp函数作用到一个参数集合上的时候,一个新的环境建立起来了,函数和它的参数 在这个环境里建立起来。然后,函数体里的表达式在这个环境里求值。
练习 3.5
略。
3.5.2 局部变量
定义函数是设置局部环境的一个方法,该环境用来计算一个表达式集合,也就是函数体。另一个方法就是使用特殊形式let,这在上边的第2.7节简单介绍过。let表达式的一般语法是:
(let ((<var 1> <e 1>)
...
(<var n> <e n>))
<body>)
当let表达式求值的时候,值表达式<e 1>, ..., <e n>首先求值。然后一个let环境被设置成功,该环境包围了let表达式的环境组成,变量<var 1>, ..., <var n>与表达式的结果<e 1>, ..., <e n>是绑定的。最后,<body>里的表达式在这个新环境里被求值,旧的环境被保存起来。let表达式返回的结果就是<body>里最后一个表达式的求值结果。
特殊形式let在设置局部变量来简化表达式方面是非常重要的。举个简单的例子,假设我们想要定义一个函数,它带两个参数,呈现为实向量形式,然后返回其中一个向量在另一个向量上的投影。如果<x, y>表示代表x和y的内积,那么y在x上的投影可以如此给定:<x, y>/<x, x> *x。为了计算这个投影,我们可以这样定义投影函数:
> (defun project (y x)
(* (/ (sum (* x y)) (sum (* x x))) x))
PROJECT 现在,我们可以找到向量(1 3)在向量(1 1)上的投影:
> (project '(1 3) '(1 1)) (2 2)project函数的函数体不算太复杂,但是我们可以通过将两个内积写成一个局部变量进一步简化表达式。
> (defun project (y x)
(let ((ip-xy (sum (* x y)))
(ip-xx (sum (* x x))))
(* (/ ip-xy ip-xx) x))) PROJECT 设置局部变量ip-xy和ip-xx来表示<x, y>和<x, x>的内积,在let表达式体里用来计算投影值。这个表达式与上边给出的数学表达式很接近,很容易检查。
关于let的一个重点是,它构造的绑定是并行的。新的局部变量的值相对的表达式在包围他们的环境中被计算,然后再设置绑定,为了说明这一点,让我们看一个简单的,人造的例子:
> (defun f (x)
(let ((x (/ x 2))
(y (+ x 1)))
(* x y)))
F 使用参数4来调用这个表达式的结果是:
> (f 4) 10首先,这个结果可能让人吃惊,你可能认为结果是6.但是如果你使用这里给定的求值规则该函数就会有意义。变量x在(/ x 2)和(+ x 1)两个表达式里均被引用,x是在let环境里的,该变量对应f函数的参数。当对表达式(f 4)求值时,该变量的值是4。一旦这两个表达式求值时,一个新的环境就建立了,其中x与2绑定,y与5绑定。这个对x的新的绑定覆盖了来自周围环境的绑定,该变量的旧值在离开let表达式体的时候仍然是有效的。let表达式的值就是在这种绑定条件下的(* x y)的值,因此该值是10。
在序列化地设置局部变量的时候有时是有用的,即首先定义一个变量,然后在第一个变量后定义第二个变量。在project函数的定义里,我们可能想要定义一个变量来表示x的系数,比如以内积变量的论。由于let绑定的并行分配,这些可以使用一个单独的let表达式完成,但是这可能需要使用连个小括号:
> (defun project (y x)
(let ((ip-xy (sum (* x y)))
(ip-xx (sum (* x x))))
(let ((coef (/ ip-xy ip-xx)))
(* coef x)))) 这是个共性问题,Lisp提供了一个简单地方法。特殊相识let*与let的工作方式类似,除了它每次都会向所在的环境进行绑定,然后计算在一个环境里对表达式求值,包括目前构造的所有的绑定。使用let*,我们可以讲函数写成:
> (defun project (y x)
(let* ((ip-xy (sum (* x y)))
(ip-xx (sum (* x x)))
(coef (/ ip-xy ip-xx)))
(* coef x)))
PROJECT 在上边那个人工的案例里,如果我们使用let*来代替let,那么:
> (defun f (x)
(let* ((x (/ x 2))
(y (+ x 1)))
(* x y)))
F 然后,结果应该就是6:
> (f 4) 6
3.5.3 局部函数
除了变量绑定之外,环境也包含函数绑定。目前为止,我们已经通过使用defun来定义全局函数绑定。特殊形式flet可以用来建立局部函数定义,该定义仅在flet表达式内部是可见的。它允许你以辅助函数的形式定义一个函数,而不需要担心与其它全局函数的命名冲突。
flet表达式的一般形式如下:
(flet ((<name 1> <parameters 1> <body 1>)
...
(<name n> <parameters n> <body n>))
<body>)
符号<name 1>, ..., <name n>是局部函数的名字,列表<parameters 1>, ..., <parameters n>是参数列表,<body 1>, ..., <body n>是组成函数体的表达式或表达式序列。
举个例子,我们可以使用另一种方式编写我们的project函数。不使用局部变量表示内积,而使用一个叫ip的局部内积函数来表示:
> (defun project (y x)
(flet ((ip (x y) (sum (* x y))))
(* (/ (ip x y) (ip x x)) x)))
PROJECT 与let类似,flet在包围它的环境里并行地构建绑定,这表示使用一个具体的flet定义的函数都不能互相引用,也不能自引用。为了定义第二个局部函数coef,在ip函数里我们不得不使用第二个flet:
> (defun project (y x)
(flet ((ip (x y) (sum (* x y))))
(flet ((coef (x y) (/ (ip x y) (ip x x))))
(* (coef x y) x))))
PROJECT Lisp还提供了一个简单的替换符——特殊形式labels。就像let*一样,labels顺序地定义它的绑定,允许每一个函数引用前边定义的函数,或者引用其自身。那么labels允许你定义一个递归的局部函数。对于我们的project函数我们可以这样使用labels:
> (defun project (y x)
(labels ((ip (x y) (sum (* x y)))
(coef (x y) (/ (ip x y) (ip x x))))
(* (coef x y) x)))
PROJECT
3.6 作为数据的函数和表达式
Lisp最强大的能力就是能将函数作为数据,来构建新的自定义函数。本节介绍一些利用这项能力的函数和技术。
3.6.1 匿名函数
在第2.7节,我们绘制了函数f(x)=2x+x²在区间[-2, 3]上的图形,我们首先定义了函数f:
> (defun f (x) (+ (* 2 x) (^ x 2))) F然后计算表达式(plot-function #'f -2 3)。
一旦我们绘制出图形,我们就不再使用函数f了。如果我们能避免正式地定义函数和必须为它想个名字的话,似乎是件极好的事儿。相同的问题在数学里也存在:为了描述我要绘制的函数曲线,我引入了"函数f(x)=2x+x²"。为了解决这个问题,逻辑学家开发了lambda演算,允许你使用如下表达式: λ(x)(2x+x²)来引用“对于参数x的返回值为2x+x²的函数”这一表述。Lisp也采用了这一方法,允许函数描述成lambda表达式,一个由符号lambda组成的列表,一个参数列表,和组成函数体的一个或多个表达式。我们这个函数的lambda表达式形式如下:
> (lambda (x) (+ (* 2 x) (^ x 2))) #<Closure: #142d008>因为使用λ表达式描述的函数没有名字,它们有时叫做匿名函数。
lambda表达式可以用来替换符号,作为传给解释器的表达式的第一个元素:
> ((lambda (x) (+ (* 2 x) (^ x 2))) 1) 3lambda表达式可以作为参数传递给类似plot-function这样的函数。这个匿名函数需要通过首先与当前环境的组合来完成,然后用来确定自由变量的值。这个组合叫做函数闭包,或者简称闭包。闭包将使用特殊形式function来构造,或者它的缩写形式#'。那么,为了绘制我们的函数,我们应该使用如下表达式:
> (plot-function #'(lambda (x) (+ (* 2 x) (^ x 2))) -2 3) #<Object: 1429688, prototype = SCATTERPLOT-PROTO>连接函数闭包里的环境和函数定义的能力,是一项极其强大的编程工具。然而,为了能够充分利用该想法的优势,我们需要检测如何定义一个接受函数作为参数的函数。
3.6.2 使用函数参数
假设我们想要近似一个积分值:
一个方法就是使用第3.4节介绍的do结构,来定义一个积分函数:
> (defun integral (a b h)
(do ((itegral 0 (+ integral (* h (f x))))
(x (+ a (/ h 2)) (+ x h)))
((> x b) integral)))
INTEGRAL 这个定义假设有一个全局定义的函数f,它将计算被积分函数。例如,为了计算x²在区间[0, 1]上的积分,我们可以这样定义函数f:
> (defun f (x) (^ x 2)) F然后使用integral函数计算积分:
> (integral 0 1 .01) 0.333325最好设计一个接受被积分函数作为参数。为了能够做到这一点,我们需要知道如何使用这个函数参数。首先,我们可以这样定位integral函数:
> (defun integral (f a b h)
(do ((integral 0 (+ integral (* h (f x))))
(x (+ a (/ h 2)) (+ x h)))
((> x b) integral)))
INTEGRAL 然后使用如下表达式进行积分:
> (integral #'(lambda (x) (^ x 2)) 0 1 .01) 0.3333250000000004不幸的是,该表达式不起作用。原因是局部变量f将我们的函数作为它的值,而不是作为函数定义。(注:我在Lisp-Stat上运行是没有问题的,不知作者为什么这么说!!!)
相反地,我们可以使用funcall函数,这个函数带一个函数参数,还有很多该函数参数需要的参数,并将该函数参数作用到这些参数上。这里有个例子:
> (funcall #'(lambda (x) (^ x 2)) 2) 4 > (funcall #'+ 1 2) 3使用funcall函数,我们可以这样定义integral函数:
> (defun integral (f a b h)
(do ((integral 0 (+ integral (* h (funcall f x))))
(x (+ a (/ h 2)) (+ x h)))
((> x b) integral)))
INTEGRAL 该定义将按我们想要的方式运行:
> (integral #'(lambda (x) (^ x 2)) 0 1 0.01) 0.3333250000000004当你提前知道函数参数需要带几个参数的时候,函数funcall是很有用的。如果你不知道,或者如果函数带可变数量的参数的时候,那么你可以使用函数apply。这个函数带一个函数参数和这个函数参数需要的参数列表,使用这个函数,返回结果。这里有几个例子:
> (apply #'+ (list 1 2)) 3 > (apply #'+ (list 1 2 3)) 6在函数参数和列表之间插入一定数量的额外测参数是可能的。这些参数将按给定的按顺序传递给函数,要比列表里的参数提前。例如:
> (apply #'+ 1 2 (list 3 4 5)) 15在下一章里,给技术将被证明是有用的。
使用函数funcall和apply有一些限制。它们仅能通过传递函数参数来使用,而不能通过特殊形式和宏。此外,大多数Lisp系统设置了可以传递给函数的参数的数量上限。尽管在一些系统里这个限值可能很大,Common Lisp规范要求这个限值至少是50。这意味着这不是一个好主意,比如说,定义一个计算列表里元素的和的函数:
> (defun my-sum (x) (apply #'+ x))这个定义对小列表起作用,但对大列表没作用。apply和funcall函数也能接收符号作为他们的参数。这些符号的函数定义将在全局环境里确定。
练习 3.6
略。
3.6.3 作为结果的返回函数
现在我们已经见过如何使用函数参数,我们返回到函数闭包的使用上。在3.5节我们定义了一个函数project来计算y在x上的投影。思考数学投影问题的另一个方法是以投影操作符的形式思考,该操作符接受任意矢量y并将其放到关于x的投影上去。我们将用Px表示这个操作符,或者简写为P,并将y在x上的投影表示为Py。该操作符被视为一个单参数函数。被投影到的那个空间,被x跨越的空间,以某种方式“内建”到P里。在Lisp里我们可以使用函数闭包构建这个投影操作符的模型。首先,我么构建一个函数make-projection,它带一个表示数学矢量的列表x,并返回一个函数闭包,该闭包计算参数在x上的投影:
> (defun make-projection (x)
(flet ((ip (x y) (sum (* x y))))
#'(lambda (y) (* x (/ (ip x y) (ip x x))))))
MAKE-PROJECTION lambda表达式用来构建一个包含自由变量x的结果。lambda表达式所在的环境转换成一个闭包。x引用了
在调用make-projection函数的时候那个参数,那么make-projection函数返回的函数闭包“记住”了要投影的那个矢量。举个例子,有一个4维的可以被投影的常矢量,然后定义一个投影操作符投影其上:
> (def p (make-projection '(1 1 1 1))) P该投影操作符是符号p的值,所以我们不得不使用该操作符作为apply和funcall函数的参数:
> (funcall p '(1 2 3 4)) (2.5 2.5 2.5 2.5) > (funcall p '(-1 1 1 -1)) (0 0 0 0)代替使用一个lambda表达式来构建我们的结果,我们也可以使用一个局部函数。为了使这个局部函数允许使用内积函数ip,我们不得不也使用一个带小括号的flet表达式或者一个labels表达式,就像这样:
> (defun make-projection (x)
(labels ((ip (x y) (sum (* x y)))
(proj (y) (* x (/ (ip x y) (ip x x)))))
#'proj))
MAKE-PROJECTION 练习 3.7
略。
练习 3.8
略。
3.6.4 作为数据的表达式
代替使用函数参数,有时使用表达式更加方便。一个作何的Lisp表达式只不过是一个Lisp列表。它的元素可以使用select函数或者函数first、second, ..., tenth来提取:
> (def expr '(+ 2 3)) EXPR > (first expr) + > (second expr) 2另一个检测表达式的有用的函数是rest,这个函数带一个列表作为参数,并且返回一个除了第一个元素的列表:
> (rest expr) (2 3)函数eval可以对一个表达式求值:
> (eval expr) 5函数eval在全局环境里进行求值,那么如果你的表达式包含任何变量,这些变量的全局值将被使用:
> (def x 3) X > (let ((x 5)) (eval 'x)) 3如果你想在一个表达式求值之前,用一个特定值替换掉表达式里的变量,你可以使用函数subst:
> (def expr2 '(+ x 3)) EXPR2 > (eval (subst 2 'x expr2)) 5事实上,subst函数将使用第一个参数代替第二个参数的所有资源指引,不顾及语法问题。这可能会导致一些无意义的表达式:
> (subst 2 'x '(let ((x 3)) x)) (LET ((2 3)) 2)一个替代表达式就是构建一个包围你的表达式的let表达式,然后将它传递给eval:
> (list 'let '((x 2)) expr2) (LET ((X 2)) (+ X 3)) > (eval (list 'let '((x 2)) expr2)) 5创建一个列表模板,该模板里只有很少表达式被引用,我们来向模板里填入内容,这一过程是相当普遍的。Lisp又一次提供了一个简写,一个置于列表之前的反引号将导致列表里的所有元素被引用,除了那些前面加了逗号的元素:
> `(let ((x 2)) ,expr2) (LET ((X 2)) (+ X 3)) > (eval `(let ((x 2)) ,expr2)) 5都好不能出现在加反引号的那个列表的顶层,但是可以包含在其子列表里:
> `(let ((x ,(- 3 1))) ,expr2) (LET ((X 2)) (+ X 3))举个例子,我们可以构建一个简单的函数,用来绘制一个矢量表达式相对于一个变量值的图形。如果我们调用函数plot-expr,然后(plot-expr '(+ (* 2 x) (^ x 2)) 'x -2 3)表达式应该产生一个2x+x²在区间[-2, 3]上的图形。使用反引号机制,我们可以这样定义这个函数:
> (defun plot-expr (expr var low high)
(flet ((f (x) (eval `(let ((,var ,x)) ,expr))))
(plot-function #'f low high)))
PLOT-EXPR 使用表达式参数而不是一个函数的优势是plot-expr函数已经获得了表达式和变量的名称,它们可以被用来为图形构建有意义的坐标标记。
3.7 映射
能够一个函数对一个列表按元素进行操作经常是非常有用的。这个处理过程叫做映射,mapcar函数可以带一个函数和一个参数列表,并且返回结果列表,该结果是函数作用到每个元素时产生的:
> (def x (mapcar #'normal-rand '(2 3 2))) X > x ((0.374662664815698 2.2129702160457247) (-0.6790406077067712 -1.5090307911933598 -0.7422588556111767) (0.2212920384039958 0.5462770527223718)) > (mapcar #'mean x) (1.2938164404307113 -0.9767767515037692 0.3837845455631838)mapcar参数可以带一些类表作为参数,被映射的函数必须带相同数量的参数。第一个元素将被传递以调用函数,然后是第二个参数,等等:
> (mapcar #'+ '(1 2 3) '(4 5 6)) (5 7 9)如果列表参数之间长度不等,那么求值过程将在最短的那个列表用尽时停止。
另一个在Lisp-Stat里可用的映射函数是map-elements。这个函数将使用组合数据和简单数据的Lisp-Stat区别。组合数据是列表、矢量、数组和组合数据对象(这个一会儿介绍)。不是组合数据的数据项将被看做是简单数据。预测函数compound-data-p可以测试一个数据是否是组合数据。
函数map-elements允许你在参数上映射一个函数,该参数可能是简单数据和组合数据的组合。如果任何一个参数是组合数据,那么任何简单数据都将被作为合适大小的常量看待。例如:
> (map-elements #'+ 1 '(1 2 3) '(4 5 6)) (6 8 10)Lisp-Stat里的所有矢量化算术函数都隐含使用一个队map-elements函数的递归调用。+函数的定义与下式较相似:
> (defun vec+ (x y)
(if (or (compound-data-p x) (compound-data-p y))
(map-elements #'vec+ x y)
(+ x y)))
VEC+ 一些例子如下:
> (vec+ 1 2) 3 > (vec+ 1 '(2 3)) (3 4) > (vec+ '(1 2) '(3 4)) (4 6) > (vec+ '(1 2) '(3 (4 5))) (4 (6 7))与mapcar函数不同,函数map-elements希望它的所有组合参数有相同数量的元素数目:
> (vec+ '(1 2) '(3 4 5)) Error: arguments not all the same length Happened in: #<Subr-MAP-ELEMENTS: #13ef154>事实上,组合参数应该是相同形状的,那么数组应该有相同的维度。
你不需要经常使用map-elements函数来定义你自己的矢量化函数,除非你需要条件计算。例如,假设你想要定义一个这样的矢量化版本:
Lisp-Stat提供了一个if-else函数,这样调用它:(if-else <x> <y> <z>),如果<x>, <y>和<z>是相同长度的列表,if-else函数返回一个同长度的列表。结果的第i个元素,或者是<y>的第i个元素,或者是<z>的第i个元素,这取决于<x>的第i个原始是non-nil还是nil。编写我们函数的简单的方法就是使用if-else:
> (defun f (x) (if-else (> x 0) (log x) 0)) F这个不起作用,因为if-else是一个函数,它所有的参数都在函数调用之前被调用了。因此在if-else改变去测试比较的的结果之前,试图用0去调用log函数将会产生一个错误。
> (defun f ()
(if (compound-data-p x)
(map-elements #'f x)
(if (> x 0) (log x)0)))
F 练习 3.9
略。
3.8 赋值和破坏性修改
在像FORTRAN和C这类编程语言里,赋值语句是编程的最基本元素。例如,在下边的factorial函数的C定义里,赋值语句用来更新局部变量prod,它是累计结果的关键一步:
int factorial(n)
{
int count;
int prod = 1;
for (count=0; count<n; count=count +1)
prod=prod * (coung + 1);
return prod;
}
这里我们不能对这段程序翻译成Lisp。我们可以设置局部变量,像prod,来给它赋一个新值,但是我们没有办法改变它们的值。也许更重要的是,我们没有赋值机制的需要。
目前为止,本章中我所完成的每一件事都是用函数式的或者可用的编程风格来完成的。更复杂的函数已经
以简单函数组合的形式构建出来了的。局部变量仅仅被定义用来简化表达式。当我们替换了在let表达式里创建的局部变量的时候,我们的函数的意思不应该改变,例如,即使函数定义因此变模糊了,其意义也不应改变。相对地,针对factorial的C程序使用了局部变量prod作为存储位置。使用它的初始值1代替每一个位置的prod变量都会产生废话。
使用局部变量来定义,而不通过赋值的方式改变它的值,这种编程风格叫做引用透明。事实上,无论什么时候可能,使用这种风格都有很好的理由。简而言之,一个程序使用赋值符是正确的,不使用就是不正确的,这句话很难通过构建一个数学证明来验证。Abelson和Sussman详尽地讨论了这个问题。
然而,赋值操作确实有一些重要的应用。例如,我们可能想在计算机屏幕上构建一个窗体的软件表示。窗体可能又各种各样的属性,像它的尺寸和位置,这些可以记录成本地状态变量。作为一个带窗体的用户接口,它可以移动和调整尺寸,为了保持一直是最新的表示法,我们需要能够改变这些状态变量,给他们赋新值。
在Lisp里,基本的赋值工具是特殊形式setf。setf可以改变全局变量和局部变量的值。例如,
> (setf x 3) 3 > x 3
> (let ((x 1))
(setf x 2)
x)
2 传给setf的第一个参数不会被求值,所以符号x不需要被引用。不像setf,def只影响全局绑定。
一个问题的例子是随机数字生成器,在这个问题里我们需要能够修改一个状态变量。一个线性同余生成器需要由一个种子X0,一个乘法器A和一个系数M来制定,这些都是正整数。它根据规则:![]() 来计算伪随机整数序列X1, X2,...。一个近似正态的伪随机序列U1, U2, ...,这样产生:Ui=Xi/M。
来计算伪随机整数序列X1, X2,...。一个近似正态的伪随机序列U1, U2, ...,这样产生:Ui=Xi/M。
通过使用包含乘法器、系数和当前X值的函数闭包,我们能够实现这样一个生成器。X的当前值是状态变量,每次它都会更新成获得的新的数字。函数make-generator构建了这样一个闭包:
> (defun make-generator (a m x0)
(let ((x x0))
#'(lambda ()
(setf x (rem (* a x) m))
(/ x m))))
MAKE-GENERATOR
函数rem计算第一个参数被第二个参数除后的余数。该定义中lambda表达式体包含两个表达式,第一个是个赋值表达式,用来产生局部变量x的变化的值得副作用(注:这里的副作用是针对函数式风格说的!!!)。第二个表达式在生成器被使用时返回结果。这个lambda表达式没有带参数。
通过使用A=7的五次方,系数M=2的31次方-1,种子为12345,我们能够构造和尝试一个特定的生成器:
(def g (make-generator (^ 7.0 5) (- (^ 2.0 31) 1) 12345))
> (funcall g) 0.09661652850760917 > (funcall g) 0.8339946273872604 > (funcall g) 0.9477024976851895
因为由make-generator返回的函数不需要任何参数,funcall函数除了生成器g之外不需要其它参数。环境里的局部状态变量x,闭包g就是在那个环境里创建的,每当g被调用的时候x更新。结果,每次对g的调用都会返回不同的值。赋值操作可以用来以程序的风格编写程序。例如,现在我们可以将本节开头的C版本的factorial函数,翻译成Lisp版本:
> (defun factorial (n)
(let ((prod 1))
(dotimes (count n)
(setf prod (* prod (+ count 1))))
prod))
FACTORIAL dotimes结构在第2.5.6节就有简单介绍了,随着count值从0增长到n-1,dotimes的结构体重复执行n次。
像我们在2.4.5节看到的,setf可以通过改变列表里元素的值来破坏性地修改一个列表。例如,如果x被构建成这样:
> (setf x (list 1 2 3))我们可以使用下边的表达式来改变其第二个元素,该元素的索引(即下标)为1:
(setf (select x 1) 'a)setf表达式里的(select x 1)叫做位置形式(注:此处翻译可能不准确,原文是a place form,意思应该是选择列表的某一位置的元素的操作),或者叫广义变量。可用的位置形式还有很多,并且定义新的位置形式或者setf方法也是可能的。这个在下一章里将进一步讨论。
值得我们再次关注的是,Lisp变量仅仅为数据项的名字,破坏性的修改可能带来不可预期的副作用。尤其地,如果x这样构建:(setf x '(1 2 3)),y这样定义:(setf y x),那么修改x的值将修改y的值,因为这些符号只不过是它们引用的相同的Lisp数据项的两个不同的名字而已。
> (setf (select x 1) 'a) A > x (1 A 3) > (setf y x) (1 A 3) > y (1 A 3)在修改之前,你可以使用copy-list函数对x做一份拷贝。
3.9 等价
当两个Lisp数据项被视为相同的时候,很多函数需要来确定这个判断。这就发生了一件微妙的事情,尤其在介绍了赋值之后。两个事物是否等价,依赖于使用它们完成了什么。字符串“fred”和“Fred”可能被看做是不同的,因为它们包含不同的字符串。它们可能被视为是相同的,因为它们都能拼出Fred这个名字。当你把一个符号的名字键入到Lisp解释器的时候,字母的大小写是被忽略的。对于这个目的,上边的两个字符串是相同的。如果使用这些字符的ASCII码来计算字符串的编码,你会对这两个字符串计算出两个不同的结果。对于这个目的,这两个字符串是不同的。
另一个例子,假设你有两个列表,都打印成这样: (A B),它们是等价的吗?如果你仅仅是想提取它们的元素,那么这两个字符串后返回相同的结果,因此它们可能被看做相同。换句话说,随着setf的引入,我们可以物理地修改一个列表的内容。假设我们这么做了,那另一个列表也会受影响吗?这取决于它们是否处于相同的计算机内存位置。
为了解决这种情况,Lisp提供了4个不同严格等级的等价谓词。最严格的的是eq。当且仅当它们处于内存的相同位置的时候,它们才是eq的。这是我们想要的测试,用来确保在修改它们中的一个之前我们的两个列表是真的不同。
当解释器将一个字符串翻译成一个符号时,可以保证的是相同名字的两个符号是eq的。
一个密切相关的谓词是eql。eq与eql之间唯一的不同是eql将考虑以下几项指标,相同类型和值的数量,有相同值和大小写情况的字符,在相同的大小写情况下的有相同字符的字符串。依据Lisp实现,它们可能是eq的也可能不是eq的。如此,对一些Lisp实现,(eq 1 1)可能返回t,而对另一些则返回nil,但是(eql 1 1)始终返回t,换句话说,
> (eq (list 'a 'b) (list 'a 'b)) NIL > (eql (list 'a 'b) (list 'a 'b)) NIL > (eq 1 1.0) NIL > (eql 1 1.0) NIL对list的两次调用返回了不同的列表,整数1和浮点数1.0是不同的数据类型。
谓词equal和equalp用来确定两个数据项是否看起来很相似。如果(eql x y)返回t,或者x与y的程度相等所有元素也对应相等,那么表达式(equal x y)返回t。equalp谓词词性比equal略弱,如果两个数的数值是相等的,那么equalp就认为他们是equalp相等的,无论类型是否相同。如果两个字符串有相同的字符,无论大小写是否相同,它们是equalp相等的。那么:
> (equal (list 'a 'b) (list 'a 'b)) T > (equalp (list 'a 'b) (list 'a 'b)) T > (equalp 1 1.0) T > (equal 1 1.0) NIL > (equal "fred" "Fred") NIL > (equalp "fred" "Fred") T一些函数需要测试列表之间对应元素的等价性,比如3.6.4节里介绍的subst函数。默认情况下这些函数使用eql测试。可以使用一个关键字参数来覆盖这个默认值(见4.4节)。
3.10 一些例子
本章介绍了大量的新想法和技术。在继续深入之前,看一些更广泛的例子是很有帮助的,这些例子动用了这里表达的一些技术。第一个例子使用牛顿法求解一个函数的变量的平方根。第二个例子展示了一个构建表征区别的方法。
3.10.1 牛顿法求根
牛顿法求解可微函数f的根,该法带一个猜测值y,并这样计算一个改进的猜测值:y-f(y)/Df(y),这里的Df表示f的导数。通过对如下形式的递归定义,基本的迭代可以沿着3.4节里的平方根的方法开发:
> (defun newton-search (f df guess)
(if (good-enough-p guess f df)
guess
(newton-search f df (improve guess f df))))
NEWTON-SEARCH 或者通过使用do结构:
> (defun newton-search (f df guess)
(do ((guess-guess (improve guess f df)))
((good-enough-p guess f df) guess)))
NEWTON-SEARCH 函数improve和good-enough-p可定义成这样:
> (defun improve (guess f df)
(- guess (/ (funcall f guess) (funcall df guess))))
IMPROVE
> (defun good-enoungh-p (guess f df)
(< (abc (funcall f guess)) 0.001))
GOOD-ENOUNGH-P 作为检核,我们可以使用newton-search,来求sin(x)在3附近的值时π的值:
> (newton-search #'sin #'cos 3) 3.14255newton-search函数的定义有一些缺陷,尤其地,improve和good-enough-p的定义可能会干扰到其它定义,就像为了求解平方根问题我们所做的设置那样。为了避免这些困难,我们可以使用flet建立一个块结构:
> (defun newton-search (f df guess)
(flet ((improve (guess f df)
(- guess
(/ (funcall f guess)
(funcall df guess))))
(good-enough-p (guess f df)
(< (abs (funcall f guess)) .0.001)))
(do ((guess guess (improve guess f df)))
((good-enough-p guess f df) guess))))
NEWTON-SEARCH 函数improve和good-enough-p仅在newton-search体里是可见的。
通过将improve和good-enough-p函数移动到newton-search函数里,我们可以进行一点简化。因为f和df在improve哈good-enough-p函数定义的那个环境里是可用的,所以我们不需要将它们作为参数传递:
> (defun newton-search (f df guess)
(flet ((improve (guess)
(- guess
(/ (funcall f guess)
(funcall df guess))))
(good-enough-p (guess)
(< (abs (funcall f guess)) .001)))
(do ((guess guess (improve guess)))
((good-enough-p guess) guess))))
NEWTON-SEARCH 正确地找出导数通常是个问题。因为对于牛顿法来说,数值的导数通常足够精确了。我们可以重写newton-search函数来使用数值导数进行计算。但是这也意味着当我们确实有可用的导数的时候,我们就不能利用这个精确的导数了。一个替代物就是构建一个可以产生数值导数的函数:
> (defun make-derivative (f h)
#'(lambda (x)
(let ((fx+ (funcall f (+ x h)))
(fx- (funcall f (- x h)))
(2h (* 2 h)))
(/ (- fx+ fx-) 2h))))
MAKE-DERIVATION make-derivation函数返回的结果是一个函数闭包,该闭包用来记忆在计算数值导数中用到的函数f和步长h。当这个函数使用一个参数x定义的时候,他将使用函数f在x的对称差商来逼近其导数。现在我们可以使用make-derivative函数来为函数newton-search提供导数这个参数:
> (newton-search #'sin (make-derivative #'sin .001) 3) 3.1425465668320545我们也可以使用newton-search和make-derivate函数,通过查找其一阶导数的根的方法,来定位函数的最大值。举个例子,假设我们想要找到γ-分布里的指数的极大似然估计,该分布的尺度函数参数是1。我们可以从指数α=4.5的γ-分布里生成一组数据样本,然后把它赋给变量x:
> (def x (gamma-rand 30 4.5)) X其log似然估计可以写成这样:(α-1)s - n log Γ(α),其中s=ΣlogXi,是充分的统计量,n是样本大小。
估计这个log似然度的函数可以这样构建:
> (def f (let ((s (sum (log x)))
(n (length x)))
#'(lambda (a)
(- (* (- a 1) s) (* n (log-gamma a))))))
F 这个函数是变量f的值,包围lambda表达式的let语句用来创建一个环境,在这个环境里变量s和n表示足够的统计样本和样本大小,对我们的样本来说他们绑定到合适的值上。生成这个函数闭包的过程这个数学处理过程是类似的,该数学处理过程发生在一旦获取样本数据时,抑制对数据的对数似然的依赖性。
为了使用newton-search函数找到α的最大似然估计,我们需要对数似然函数的一阶导数和二阶导数。这些可以这样获取:
> (def df (make-derivative f .001)) DF > (def ddf (make-derivative df .001)) DDF对极大似然估计量我们还需要一个初始猜测,因为γ-分布的尺度参数是1,α的矩估计方法就是样本均值:
> (mean x) 4.683152258151905现在我们可以找到最大似然估计量了:
> (newton-search df ddf (mean x)) 4.747512880561235练习 3.10
略。
3.10.2 符号微分
符号微分化使用微分计算的规则来表达和产生表示导数的表达式。起初它看起来可能是令人吃惊的,但事实上自动地使用这些规则来开发程序是相当简单的。最难的那部分就是确定如何通过这样一个程序来表达使用的数据:被微分的表达式和表示导数的表达式。
为了保持简洁,让我们以微积分类可能的开始方式,通过考虑仅针对微分常量、变量、和还有乘积的规则,开始我们的讨论。
抽象表达式
微分函数使用的数据就是表达式。有很多不同的方式,这些方式不能用计算机来表达,但是表达式的细节与微分式要表现的基本任务几乎没有关系。为了反映这个事实,简要地想一想用来开发微分函数所需要的表达式的精确特征,还有用来捕获这些特征的函数集合,想清楚以上两点是非常重要的。这个函数集合叫做抽象数据表示法,它可以用来编写我们的微分函数。过会儿,我们能够用开发这个数据表示的不同的方式来进行试验。但是,通过将表达式的使用从他们的表示的内部细节中分离出来,我们将获得一个系统,该系统比数据表示与数据使用交织在一起的方法更容易理解和修改。这个编程策略叫做数据抽象。
在我们的函数式表达方法中,我们需要表示的表达式的基本特征是什么呢?首先,有四种数据类型:常量、变量、加法和乘积。我们需要能够识别一个特定的数据项是不是这四种数据类型中的一个。让我们做个假设:为这个目的我们可以定义四个谓词:
(constantp <e>) (varialbep <e>) (sump <e>) (productp <e>)我们还需要另一个谓词,用来识别两个变量是否相同,
(same-variable-p <v1> <v2>)
常量和变量时原子表达式,它们不能被分解或者由其它表达式构建。相反,加法和乘积是组合表达啥。因此我们需要“访问函数”来提取它们的各部分构件,需要构造函数来构建新的加法和乘积。加法的各部分构件是加数和被加数。假设我们可以用以下表达式获取:
(addend <e>) (augend <e>)然后我们可以构建一个新的加法:
(make-sum <a1> <a2>)乘积的各部分构件是被乘数和乘数,它们可以这样获得:
(multiplicand <e>) (multiplier <e>)一个新的乘积可以这样构建:
(make-product <m1> <m2>)这些是所有的我们用来描述微分处理的函数:
> (defun deriv (exp var)
(cond
((constantp exp) 0)
((variablep exp) (if (same-variable-p exp var) 1 0))
((sump exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((productp exp)
(make-sum (make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(t (error "Can't differentiate this expression")))) error函数用来如果没有可用的微分规则时发出一个错误信号,那个字符串参数就是错误信息。
函数deriv表示微积分课程里涵盖的前几个微分法则的简单的Lisp编码。例如,加法法则的Lisp编码为:
表达式如何实现的细节是不重要的,只要他们符合这里使用的函数式抽象的接口就可以了。在我们能使用这个函数之前,我们确实需要开发至少一个表示法用来表达。
一个用来表达的表示法
表示表达式有很多方法,但是最容易的方法就是使用标准Lisp语法,常量由数字表示,变量由符号表示。
让我们从定义加法规则和乘积规则的“读取函数”和“构造函数”。对于加法规则我们定义:
> (defun addend (e) (second e)) ADDEND > (defun augend (e) (third e)) AUGEND > (defun make-sum (a1 a2) (list '+ a1 a2)) MAKE-SUM
对于乘积法则:
> (defun multiplier (e) (second e)) MULTIPLIER > (defun multiplicand (e) (third e)) MULTIPLICAND > (defun make-product (m1 m2) (list '* m1 m2)) MAKE-PRODUCT测试一个数据项是常量还是变量的谓词相当简单:
> (defun constantp (e) (numberp e)) CONSTANTP > (defun variablep (e) (symbolp e)) VARIABLEP测试两个变量是否相同的谓词也很简单:
> (defun same-variable-p (v1 v2)
(and (variablep v1) (variablep v2) (eq v1 v2)))
SAME-VARIABLE-P 我们使用eq谓词是因为当且仅当两个符号eq等价时,它们才是相同的。
对加法规则和乘积规则进行测试的谓词就稍微复杂一些了。我们需要检查一个数据项是否是三元素的列表,它们的开始元素是+或者*。那么对于加法规则有:
> (defun sump (e)
(and (listp e) (= (length e) 3) (eq (first e) '+)))
SUMP
对于乘积规则有:
> (defun productp (e)
(and (listp e) (= (length e) 3) (eq (first e) '*)))
PRODUCTP
现在我们可以用一些例子测试一下我们的导数函数:
> (deriv '(+ x 3) 'x) (+ 1 0) > (deriv '(* x y) 'x) (+ (* X 0) (* 1 Y)) > (deriv '(* (* x y) (+ x 3)) 'x) (+ (* (* X Y) (+ 1 0)) (* (+ (* X 0) (* 1 Y)) (+ X 3)))结果是正确的,但是与需要相比它们还是太复杂了。不幸的是,简化一个表达式是一项比微分计算还要困难的任务,首要的是因为不太容易陈述一个表达式比另一个简单了究竟意味着什么。然而,通过编写函数将加法规则和乘积规则更加智能一点,我们能略微改善我们的微分算子。在make-sum函数的定义里,我们将检查如果所有的参数都是数字,那么返回它们的和。如果其中一个参数是0,我们可以只返回其它参数:
> (defun make-sum (a1 a2)
(cond
((and (numberp a1) (numberp a2)) (+ a1 a2))
((numberp a1) (if (= a1 0) a2 (list '+ a1 a2)))
((numberp a2) (if (= a2 0) a1 (list '+ a1 a2)))
(t (list '+ a1 a2))))
MAKE-SUM
相似地,对于make-product函数,如果两个参数都是数字就返回他们的乘积,如果其中一个为零就返回零,如果其中一个为1,则返回另一个参数的数值:
> (defun make-product (m1 m2)
(cond
((and (numberp m1) (numberp m2)) (* m1 m2))
((numberp m1)
(cond ((= m1 0) 0)
((= m1 1) m2)
(t (list '* m1 m2))))
((numberp m2)
(cond ((= m2 0) 0)
((= m2 1) m1)
(t (list '* m1 m2))))
(t (list '* m1 m2))))
MAKE-PRODUCT
现在结果更合理一些,尽管还不完美:
> (deriv '(+ x 3) 'x) 1 > (deriv '(* x y) 'x) Y > (deriv '(* (* x y) (+ x 3)) 'x) (+ (* X Y) (* Y (+ X 3)))练习 3.11 3.12 3.13
略。
加入一元函数
假设我们想要加入exp函数,不是为这个函数增加一个强制的规则来求得导数,而是最好增加一个表示链式规则的规则,然后在数据表示里,将这个特定的函数处理成微分形式。为了加入链式规则,我们需要一个谓词用以识别一个一元函数调用:
(unary-p <e>)
我们也需要“读取函数”来确定函数名和函数的参数:
(unary-function <e>) (unary-argument <e>)我们需要能够构建一个表达式在函数的参数上计算导数:
(make-unary-deriv <f> <x>)然后我们可以将deriv函数修改成这样:
> (defun deriv (exp var)
(cond
((constantp exp) 0)
((variablep exp) (if (same-variable-p exp var) 1 0))
((sump exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((productp exp)
(make-sum (make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
((unary-p exp)
(make-product (make-unary-deriv (unary-function exp)
(unary-argument exp))
(deriv (unary-argument exp) var)))
(t (error "Can't differentiate this expression"))))
DERIV 函数make-unary-deriv也可以我们的表达式的抽象表示法的方式定义。一个办法就是使用case结构:
> (defun make-unary-deriv (fcn ar)
(case fcn
(exp (make-unary 'exp arg))
(sin (make-unary 'cos arg))
(cos (make-product -1 (make-unary 'sin arg)))
(t (error "Can't differentiate this expression"))))
MAKE-UNARY-DERIV
这里的case后带一个表达式,该表达是将计算出一个符号,叫做“case选择器”,它后边紧跟真一系列的case语句。每个case语句都以一个符号或符号列表开始,然后case将按流程处理每条语句直到选择器与其中一条语句里的符号匹配为止。当发现一个匹配之后,被匹配的语句的剩余的表达式将被求值,然后其最后一个表达式的结果将被返回。如果没有发现可匹配的符号,将返回nil。符号t比较特殊:它可以匹配任何选择器。
make-unary-deriv函数需要一个额外的构造器(make-unary <f> <x>)来构造一个一元函数构造表达式。
对于我们的表达式来说,谓词和读取函数都是比较容易定义的:
> (defun unary-p (e)
(and (listp e) (= (length e) 2)))
UNARY-P
> (defun unary-function (e) (first e))
UNARY-FUNCTION
> (defun unary-argument (e) (second e))
UNARY-ARGUMENT 谓词unary-p的定义不是很完美,但是对目前的应用来说已经足够了。构造函数make-unary也很简单:
> (defun make-unary (fcn arg) (list fcn arg)) MAKE-UNARY为了保证这个新的规则可以正常工作,让我们测试一些例子:
> (deriv '(exp (* 3 x)) 'x) (* (EXP (* 3 X)) 3) > (deriv '(sin (* 3 x)) 'x) (* (COS (* 3 X)) 3)使用规则库
这个方法的一个方面是不太令人满意的。就像你在用deriv函数一样,增加一些函数可能是你想要做的事情。现在,需要编辑make-unary-deriv函数。一个可以替代的办法就是设置一个导数数据库。让我们做一个假设,我们有一个包含处理一元函数的规则的数据库,这些规则可以使用函数get-unary-rule来查询得到。函数apply-unary-rule用来将一个规则作为参数,去产生一个通过对参数求值得到的导数表达式。我们可以这样编写make-unary-deriv函数:
> (defun make-unary-deriv (fcn arg)
(apply-unary-rule (get-unary-rule fcn) arg))
MAKE-UNARY-DERIV 为了实现我们的数据库,我们可以使用一个“关联列表”。关联列表就是列表的列表。每一个子列表以一个符号开始,作用是左右一个键。函数assoc带一个键和一个关联列表,然后返回第一个匹配键的子列表,当无匹配键时返回nil。一个简单的例子如下:
> (def *mylist* '((x 1) (y "hello") (abc a w (1 2 3)))) *MYLIST* > (assoc 'x *mylist*) (X 1) > (assoc 'y *mylist*) (Y "hello") > (assoc 'abc *mylist*) (ABC A W (1 2 3)) > (assoc 'z *mylist*) NIL让我们使用一个全局变量*derivatives*来处理我们的导数数据库。初始情况下我们的数据库是空的,所以我们将它设置为nil:
> (def *derivatives* nil) *DERIVATIVES*为了能向数据库加入数据,我们可以使用函数cons将一个元素加入到一个列表的前端,例如:
> (cons 'a '(b c)) (A B C)使用cons函数,我们能够定义函数add-unary-rule来向数据库加入规则:
> (defun add-unary-rule (f rule)
(setf *derivatives* (cons (list f rule) *derivatives*)))
ADD-UNARY-RULE 取回函数可以这样编写:
> (defun get-unary-rule (f)
(let ((rule (assoc f *derivatives*)))
(if rule
rule
(error "Can't differentiate this expression"))))
GET-UNARY-RULE 现在我们可以确定对于规则什么是可以使用的。一个简单的选择就是一个带单参数的函数,导数参数,然后返回导数表达式。那么apply-unary-rule函数就很简单了:
> (defun apply-unary-rule (entry arg)
(funcall (second entry) arg)) 我们可以使用以下方式向我们的数据库增加一些规则:
> (add-unary-rule 'exp #'(lambda (x) (make-unary 'exp x))) ((EXP #<Closure: #13b0844>)) > (add-unary-rule 'sin #'(lambda (x) (make-unary 'cos x))) ((SIN #<Closure: #13b02a4>) (EXP #<Closure: #13b0844>))现在我们可以看一些例子:
> (deriv '(exp x) 'x) (EXP X) > (deriv '(exp (* -1 (* x x))) 'x) (* (EXP (* -1 (* X X))) (* -1 (+ X X))) > (deriv '(sin (* 3 x)) 'x) (* (COS (* 3 X)) 3) > (deriv '(* (cos (* 3 x))) 'x) Error: Can't differentiate this expression Happened in: #<FSubr-IF: #1353650>我们的系统不能处理最后一个表达式,因为它不知道如何对余弦进行微分,不是一旦我们添加对余弦函数的求导规则,它就能对余弦进行微分了:
> (add-unary-rule 'cos
#'(lambda (x)
(make-product -1 (make-unary 'sin x))))
((COS #<Closure: #13ba8b0>) (SIN #<Closure: #13aff74>) (SIN #<Closure: #13b02a4>) (EXP #<Closure: #13b0844>))
> (deriv (deriv '(sin (* 3 x)) 'x) 'x)
(* (* (* -1 (SIN (* 3 X))) 3) 3) 一个行为由数据来决定,然后使用带有合适行为的行为数据库叫做数据导向编程。对一小段数据的行为进行选择的过程叫做调度(dispatching)。
练习 3.14
略。