R语言 线性回归(下)
五、广义线性回归
glm(formula, family=family.generator,data=data.frame) 函数用来做广义线性回归。其中fanily是分布族,对每个分布族都有相应的连接函数。
正态分布族的使用方法:glm(formula, family = gaussian(link = identity),data = data.frame) , link指定了连接函数。这个和使用lm是一样的,效率低一些。
二项分布:记一下比较重要的logistic 回归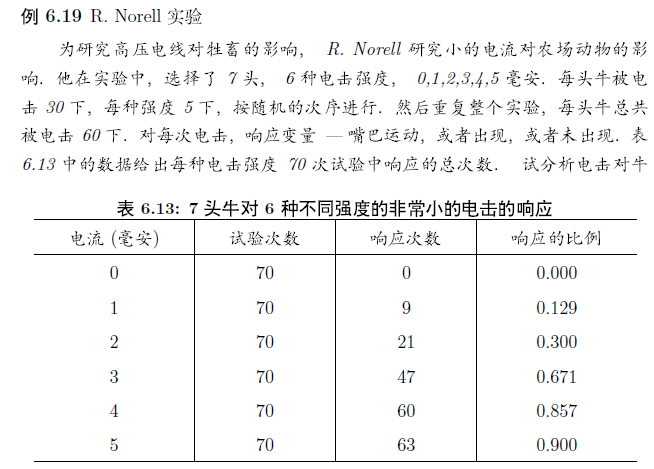
> norell <- data.frame( + x=0:5,n=rep(70,6),success=c(0,9,21,47,60,63)) > norell$Ymat <- cbind(norell$success, norell$n - norell$success) #构建一个矩阵,第一列出现次数,第二列不出现 > glm.sol <- glm(Ymat ~ x, family=binomial, data=norell) > summary(glm.sol) Call: glm(formula = Ymat ~ x, family = binomial, data = norell) Deviance Residuals: 1 2 3 4 5 6 -2.2507 0.3892 -0.1466 1.1080 0.3234 -1.6679 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -3.3010 0.3238 -10.20 <2e-16 *** x 1.2459 0.1119 11.13 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 250.4866 on 5 degrees of freedom Residual deviance: 9.3526 on 4 degrees of freedom AIC: 34.093 Number of Fisher Scoring iterations: 4 #我们得到方程 ln(p/(1-P)) = -3.3010 + 1.2459x #下面做预测 > gujizhi <- predict(glm.sol,newdata=data.frame(x=3.5)) #上面方程的估计值 > p <- exp(gujizhi)/(1+exp(gujizhi)) > p #计算出概率p 1 0.742642 #画个图看看怎么样 > x <- seq(0,5,length=100) > gujizhi <- predict(glm.sol,newdata=data.frame(x)) > p <- exp(gujizhi)/(1+exp(gujizhi)) > plot(norell$x,norell$success/norell$n) > lines(x,p) #看残差图,这个模型好像不好。不过这里我不太懂了,广义线性回归的残差是否也应该均匀分布才好
时间充裕,再来个类似的例子
考虑 Silvey (1970) 提供的一个小的例子。
在 Kalythos 的 Aegean 岛上,男性居民常常患有一种先天的眼科疾病,并且随着年龄的增长而变的愈显著。现在搜集了各种年龄段岛上男性居民的样本,同时记录了盲眼的数目。数据显示如下:
年龄: 20 35 45 55 70
No. 检测: 50 50 50 50 50
No. 盲眼: 6 17 26 37 44
我们想知道的是这些数据是否吻合 logistic 和 probit 模型,并且分别估计各个模型的 LD50,也就是一个男性居民盲眼的概率为50%时候的年龄。
如 果 y 和 n 是年龄为 x 时的盲眼数目和检测样本数目,两种模型的形式都为 y ~ B(n, F(beta_0 + beta_1 x)),其中在 probit 模型中, F(z) = Phi(z) 是标准的正态分布函数,而在 logit 模型 (默认)中, F(z) = e^z/(1+e^z)。这两种模型中, LD50 = - beta_0/beta_1 ,即分布函数的参数为0时所在的点。
第一步是把数据转换成数据框。
> kalythos <- data.frame(x = c(20,35,45,55,70), n = rep(50,5),
y = c(6,17,26,37,44))
在 glm() 拟合二项式模型时,响应变量有三种可能性:
如果响应变量是向量, 则假定操作二元(binary)数据,因此要求是0/1向量。
如果响应变量是双列矩阵,则假定第一列为试验成功的次数第二列为试验失败的次数。
如果响应变量是因子,则第一水平作为失败 (0) 考虑而其他的作为`成功'(1) 考虑。
我们采用的是第二种惯例。我们在数据框中增加了一个矩阵:
> kalythos$Ymat <- cbind(kalythos$y, kalythos$n - kalythos$y)
> fmp <- glm(Ymat ~ x, family = binomial(link=probit), data = kalythos)
> x1 <- c(2.5,173,119,10,502,4,14.4,2,40,6.6, + 21.4,2.8,2.5,6,3.5,62.2,10.8,21.6,2,3.4, + 5.1,2.4,1.7,1.1,12.8,1.2,3.5,39.7,62.4,2.4, + 34.7,28.4,0.9,30.6,5.8,6.1,2.7,4.7,128,35, + 2,8.5,2,2,4.3,244.8,4,5.1,32,1.4) > x2 <- rep(c(0,2,0,2,0,2,0,2,0,2,0,2,0,2,0,2,0,2,0,2,0,2,0) + ,c(1,4,2,2,1,1,8,1,5,1,5,1,1,1,2,1,1,1,3,1,2,1,4)) > x3 <- rep(c(0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1), + c(6,1,3,1,3,1,1,5,1,3,7,1,1,3,1,1,2,9)) > y <- rep(c(0,1,0,1),c(15,10,15,10)) > data <- data.frame(x1=x1,x2=x2,x3=x3,y=y) > glm.sol <- glm(y~x1+x2+x3,family=binomial,data=data) > summary(glm.sol) Call: glm(formula = y ~ x1 + x2 + x3, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.6960 -0.5842 -0.2828 0.7436 1.9292 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -1.696538 0.658635 -2.576 0.010000 ** x1 0.002326 0.005683 0.409 0.682308 x2 -0.792177 0.487262 -1.626 0.103998 x3 2.830373 0.793406 3.567 0.000361 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 67.301 on 49 degrees of freedom Residual deviance: 46.567 on 46 degrees of freedom AIC: 54.567 Number of Fisher Scoring iterations: 5 # x1,x2的系数并不是很显著。 用step去掉一些变量。 > glm.new <- step(glm.sol) Start: AIC=54.57 y ~ x1 + x2 + x3 Df Deviance AIC - x1 1 46.718 52.718 <none> 46.567 54.567 - x2 1 49.502 55.502 - x3 1 63.475 69.475 Step: AIC=52.72 y ~ x2 + x3 Df Deviance AIC <none> 46.718 52.718 - x2 1 49.690 53.690 - x3 1 63.504 67.504 #之后x2显著一点了 我们还可以用 influence.measures(glm.new)来检测异常点
还有其他分布族,这里就掠过了 暂时看不懂
六、非线性回归
多项式回归模型 使用上和之前的lm是一样的。照搬就好
正交多项式回归:x 要是从一次一直到多次都纳入到模型中,会造成多重共线性问题。解决办法是构造正交多项式,使他们只x有关,但相互之间是正交的。 详细原理见百度文库http://wenku.baidu.com/link?url=mJyEn8iIih2KUC2ZqiBg4-HyQc4fR__QYPQ39K_X9VODMLLBIQmBoQlDXo0KZ03wIaznJYdqIS_Rj5bSeUmD28kd6L5n9tRKEe6Z0ljSBQ_
这里没找到例子,可以看看使用方法
> lm.pol<-lm(y~1+poly(x,2),data=alloy) #poly(x,2)表示对x做2次正交 > summary(lm.pol) Call: lm(formula = y ~ 1 + poly(x, 2), data = alloy) Residuals: Min 1Q Median 3Q Max -0.33322 -0.14222 -0.07922 0.05275 0.84577 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.40923 0.09126 26.400 1.40e-10 *** poly(x, 2)1 -0.94435 0.32904 -2.870 0.016669 * poly(x, 2)2 1.74505 0.32904 5.303 0.000346 *** --- Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1 Residual standard error: 0.329 on 10 degrees of freedom Multiple R-Squared: 0.7843, Adjusted R-squared: 0.7412 F-statistic: 18.18 on 2 and 10 DF, p-value: 0.0004668 #根据这个得到的方程就是y = 2.40923 − 0.94435ϕ1 + 1.74505ϕ2. #预测还是和以前一样
其他非内在线性模型 需要使用nls(),nlm()两个函数,有时间再来看,头痛