图的广度优先遍历（BFS）

广度优先遍历是连通图的一种遍历策略。其基本思想如下：

1、从图中某个顶点V0出发，并访问此顶点；

2、从V0出发，访问V0的各个未曾访问的邻接点W1，W2，…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点；

3、重复步骤2，直到全部顶点都被访问为止。

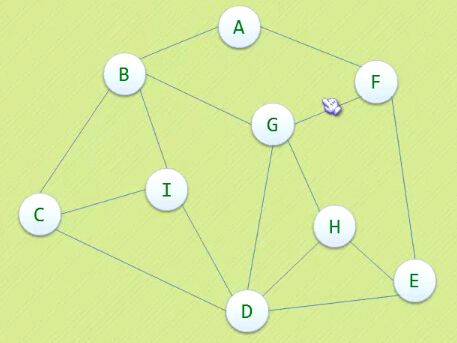
4、代码实现使用下图所示的图。

代码：

package test.algorithm.FastSlowPointer;

import java.util.LinkedList;
import java.util.Queue;

/**
 * 图的广度优先遍历
 * @author serenity
 *
 */
public class Graph2 {


	// 存储节点信息
	private char[] vertices;
	
	// 存储边信息（邻接矩阵）
	private  int[][] arcs;
	
	// 图的节点数
	private int vexnum;
	
	// 记录节点是否已被遍历
	private boolean[] visited;
	
	// 初始化
	public Graph2(int n) {
		  vexnum = n;
		  vertices = new char[n];
		  arcs = new int[n][n];
		  visited = new boolean[n];
		  for (int i = 0; i < vexnum; i++) {
		     for (int j = 0; j < vexnum; j++) {
		     arcs[i][j] = 0;
		     }
		  }

	}
	
	// 添加边(无向图)
	public void addEdge(int i, int j) {
		  // 边的头尾不能为同一节点
		  if (i == j)return;
		  
		  arcs[i][j] = 1;
		  arcs[j][i] = 1;
	}
	
	// 设置节点集
	public void setVertices(char[] vertices) {
		this.vertices = vertices;
	}
	
	// 设置节点访问标记
	public void setVisited(boolean[] visited) {
		this.visited = visited;
	}

	// 打印遍历节点
	public void visit(int i){
		System.out.print(vertices[i] + " ");
	}
	
	// 广度优先遍历
	public void BFSTraverse(){
		// 初始化节点遍历标记
		for(int i=0;i<vexnum;i++){
			visited[i] = false;
		}
		
		//创建队列
		Queue<Integer> queue = new LinkedList<Integer>();
		
		for(int i=0;i<vexnum;i++){
			if(visited[i]==false){
				// 联通子图起始节点入队
				queue.add(i);
				visited[i] = true;
				
				while(!queue.isEmpty()){
					//队列节点出队
					int curr = queue.remove();
					//打印
					visit(curr);
					
					//该节点所有还没入队的子节点在队尾
					for(int j=0;j<vexnum;j++){
						if(arcs[curr][j]==1 && visited[j]==false){
							queue.add(j);
							visited[j] = true;
						}
					}
				}
			}
		}
	}
	
	public static void main(String[] args) {
		Graph2 g = new Graph2(9);
		char[] vertices = {'A','B','C','D','E','F','G','H','I'};
		g.setVertices(vertices);
		
		g.addEdge(0, 1);
		g.addEdge(0, 5);
		g.addEdge(1, 0);
		g.addEdge(1, 2);
		g.addEdge(1, 6);
		g.addEdge(1, 8);
		g.addEdge(2, 1);
		g.addEdge(2, 3);
		g.addEdge(2, 8);
		g.addEdge(3, 2);
		g.addEdge(3, 4);
		g.addEdge(3, 6);
		g.addEdge(3, 7);
		g.addEdge(3, 8);
		g.addEdge(4, 3);
		g.addEdge(4, 5);
		g.addEdge(4, 7);
		g.addEdge(5, 0);
		g.addEdge(5, 4);
		g.addEdge(5, 6);
		g.addEdge(6, 1);
		g.addEdge(6, 3);
		g.addEdge(6, 5);
		g.addEdge(6, 7);
		g.addEdge(7, 3);
		g.addEdge(7, 4);
		g.addEdge(7, 6);
		g.addEdge(8, 1);
		g.addEdge(8, 2);
		g.addEdge(8, 3);
		
		System.out.print("广度优先遍历（递归）：");
		g.BFSTraverse();
	
	}


}