Java数据结构与算法（第五章链表）

        数组作为数据存储机构有一定的缺陷。在无序数组中，搜索是低效的；而在有序数组中，插入效率又很低；不管在哪一种数组重删除效率都很低。况且一个数组创建后，它的大小是不可改变的。

        链表可能是继数组之后第二种使用得最广泛的通用存储结构。

链结点（Link）

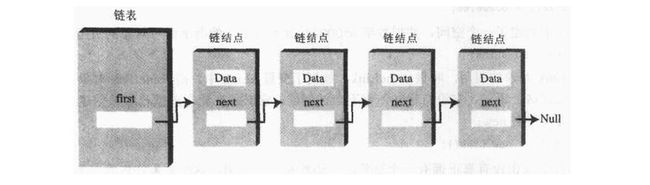
        在链表中，每个数据项都被包含在“链结点”（Link）中。一个链结点是某个类的对象，这个类可以叫做Link。因为一个链表中有许多类似的链结点，所以有必要用一个不同于链表来表达链结点。每个Link对象中都包含一个对下一个链结点引用的字段（通常叫做next）。但是链表本身的对象有一个字段指向对第一个链结点的引用。

public class Link {
    public int iData;
    public double dData;
    public Link next;
}

引用和基本类型

        在链表的环境中，很容易对“引用”产生混淆。

        在Link的类定义中定义了一个Link类型的域，这看起来很奇怪。编译器怎样才能不混淆呢？编译器在不知道一个LInk对象占多大空间的情况下，如何能知道一个包含了相同对象的Link对象占用多大空间呢？

        在Java语言中，这个wen ti的da an是Link对象并没有真正包含另外一个Link对象。看似包含了，类型的Link的next字段仅仅是对另外一个Link对象的“引用”，而不是一个对象。

关系而不是位置

        链表不同于数组的主要特性之一。在一个数组中，每一项占用一个特定的位置。这个位置可以用一个下标号直接访问。它就像一排房子，你可以凭地址找到其中特定的一间。

        在链表中，寻找一个特定的元素的唯一方法就医沿着这个元素的链一直向下找。它很想人们之间的关系。可能你问Harry，Bob在哪儿，Harry不知道，但是他想Jane可能知道，所以你又去问Jane。Jane看到Bob和Sally一起离开了公司，所以你打Sally的手机，她说她在Peter的办公室和Bob分开了，所以。。。。。。但是总有线索，不能直接访问到数据项；必须使用数据之间的关系来定位它。从第一项开始，到第二项，然后到第三个，知道发现要找的那个数据项。

‍‍单链表‍‍

双端链表

链表的效率

        在表头插入和删除速度很快。仅需要改变一两个引用值，所以花费O(1)的时间。

        平均起来，查找、删除和在指定链结点后面插入都需要搜索链表中的一半链结点。需要O(N)次比较。在数组中执行这些操作也需要O(N)次比较，但是链表仍然要快一些，因为当插入和删除链结点时，链表不需要移动任何东西。增加的效率是很显著的，特别是当复制时间远远大于比较时间的时候。

        链表比数组优越的另外一个重要方面是链表需要多少内存就可以用多少内存，并且可以扩展到所有可用内存。数组的大小在它创建的时候就固定了；所以经常有序数组太大导致效率低下，或者数组太小导致空间溢出。向量是一种可扩展的数组，它可以通过变长度解决这个问题，但是它经常只允许以固定大小的增量扩展（例如快要溢出的时候，就增加一倍数组容量）。这个解决方案在内存使用效率上来说还是要比链表的低。

抽象数据类型（ADT）

        抽象数据类型（ADT）。简单说来，它是一种kao虑数据结构的方式：着重于它做了什么，而忽略它是做么做的。

        栈和队列都是ADT的例子。前面已经看到栈和队列都可以用数组来实现。在继续ADT的讨论之前，先看一下如何用链表实现栈和队列。这个讨论将展示栈和队列的“抽象”特性：即如何脱离具体实现来kao虑栈和队列。

用链表实现栈Java代码：

package com.stack.linkstack;
public class LinkStack {
    private LinkList theList;
    public LinkStack(){
        theList = new LinkList();
    }
    public void push(long j){
        theList.insertFirst(j);
    }
    public long pop(){
        return theList.deleteFirst();
    }
    public boolean isEmpty(){
        return theList.isEmpty();
    }
    public void displayStack(){
        System.out.print("Stack (top --> bottom): ");
        theList.displayList();
    }
}
class Link{
    public long dData;
    public Link next;
    public Link(long dd){
        dData = dd;
    }
    public void displayLink(){
        System.out.print(dData+" ");
    }
}
class LinkList{
    private Link first;
    public LinkList(){
        first = null;
    }
    public boolean isEmpty(){
    return first == null;
    }
    public void insertFirst(long dd){
        Link newLink = new Link(dd);
        newLink.next = first;
        first = newLink;
    }
    public long deleteFirst(){
        Link temp = first;
        first = first.next;
        return temp.dData;
    }
    public void displayList(){
        Link current = first;
        while(current!=null){
            current.displayLink();
            current = current.next;
        }
        System.out.println("");
    }
}

public class LinkStackApp {
    public static void main(String[] args) {
        LinkStack theStack = new LinkStack();
        
        theStack.push(20);
        theStack.push(40);
        
        theStack.displayStack();
        
        theStack.push(60);
        theStack.push(80);
        
        theStack.displayStack();
        theStack.pop();
        theStack.pop();
        
        theStack.displayStack();
    }
}

//输出：
Stack (top --> bottom): 40 20 
Stack (top --> bottom): 80 60 40 20 
Stack (top --> bottom): 40 20

用链表实现队列Java代码：

package com.queue.linkqueue;
public class LinkQueue {
    private FirstLastList theList;
    public LinkQueue(){
        theList = new FirstLastList();
    }
    public boolean isEmpty(){
        return theList.isEmpty();
    }
    public void insert(long j){
        theList.insertLast(j);
    }
    public long remove(){
        return theList.deleteFirst();
    }
    public void displayQueue(){
        System.out.print("Queue (front --> rear): ");
        theList.displayList();
    }
}
class Link{
    public long dData;
    public Link next;
    public Link(long d){
        dData = d;
    }
    public void displayLink(){
        System.out.print(dData+" ");
    }
}
class FirstLastList{
    private Link first;
    private Link last;
    public FirstLastList(){
        first = null;
        last = null;
    }
    public boolean isEmpty(){
        return first == null;
    }
    public void insertLast(long dd){
        Link newlink = new Link(dd);
        if(isEmpty()){
            first = newlink;
        }else{
            last.next = newlink;
        }
        last = newlink;
    }
    public long deleteFirst(){
        long temp = first.dData;
        if(first.next==null)
            last = null;
        first = first.next;
        return temp;
    }
    public void displayList(){
        Link current = first;
        while(current!=null){
            current.displayLink();
            current = current.next;
        }
        System.out.println("");
    }
}

public class LinkQueueApp {
    public static void main(String[] args) {
        LinkQueue theQueue = new LinkQueue();
        theQueue.insert(20);
        theQueue.insert(40);
        theQueue.displayQueue();
        theQueue.insert(60);
        theQueue.insert(80);
        theQueue.displayQueue();
        theQueue.remove();
        theQueue.remove();
        theQueue.displayQueue();
    }
}
//输出：
Queue (front --> rear): 20 40 
Queue (front --> rear): 20 40 60 80 
Queue (front --> rear): 60 80

数据类型和抽象：

        “抽象数据类型”这个术语从何而来？首先看看“数据类型”这部分，再来kao虑“抽象”。

    数据类型

          “数据类型”一词用在很多地方。它首先表示内置的类型，例如int型和double型。这可能是听到这个词后首先想到的。

            当谈论一个简单类型时，实际上涉及到两件事：拥有特定特征的数据项和在数据上允许的操作。

            随着面向对象的出现，现在可以用类来创建自己的数据类型。      

            更广泛的说，当一个数据存储结构（例如栈和队列）被表示为一个类时，它也成了一个数据类型。栈和int类型在很多方面都不同，但它们都被定义为一组具有一定排列规律的数据和在此数据上的操作集合。

   抽象

            抽象是“不kao虑细节的描述和实现”。抽象是事物的本质和重要特征。

            因此，在面向对象编程中，一个抽象数据类型是一个类，且不kao虑它的实现。它是对类中数据（域）的描述和能够在数据上执行的一系列操作（方法）以及如何使用这些操作的说明。

            当“抽象数据类型”用于栈和队列这样的数据结构时，它的意义被进一步扩展了。和其他类一样，它意味着数据和在数据上执行的操作，即使子啊这种情况下，如何存储数据的基本原则对于类用户来说也是不可见的。用户不仅不知道方法怎样运作，也不知道数据是如何存储的。

    接口

            ADT有一个经常被叫做“接口”的规范。它是给类用户看的，通常是类的公有方法。在栈中push（）方法、pop（）方法和其他类似的方法形成了接口。

ADT列表

            列表（有时也叫线性表）是一组线性排列的数据项。也就是说，它们以一定的方式串接起来，像一根线上的珠子或一条街上的房子。列表支持一定的基本操作。列表支持一定的基本操作。可以插入某一项，删除某一项，还有经常从某个特定位置读出一项（例如，读出第三项）。

作为设计工具的ADT

            ADT的概念在软件设计过程总也是有用的。如果需要存储数据，那么就从kao虑需要在数据上实现的操作开始。需要存取最后一个插入的数据项？还是第一个？是特定值的项？还是在特定位置的项？回da这些问题会引出ADT的定义。只有在完整定义了ADT后，才应该kao虑细节问题，例如如何表示数据，如何编码是方法可以存取数据等等。

            当然，一旦设计好ADT，必须仔细选择内部的数据结构，以使规定的操作的效率尽可能高。例如，如果需要随机存取元素N，那么用链表表示就不够好，因为对链表来说，随机访问不是一个高效的操作。选择数组会得到较好的效果。

有序链表

            链表中，保持数据有序是有用的，具有这个特性的链表叫做“有序链表”。

            在有序链表中，数据是按照关键值有序排列的。有序链表的删除常常是只限于删除在链表头部最小（或者最大）链结点。不过，有时也用find（）方法和delete（）在整个链表中搜索某一特定点。

            一般在大多数需要使用有序数组的场合也可以使用有序链表。有序链表由于有序数组的地方是插入的速度（因为元素不需要移动），另外链表可以扩展全部有效的使用内存，而数组只能局限于一个固定的大小。但是，有序链表实现起来比有序数组更困难一些。

            后面有一个有序链表的应用：为数据排序。有序链表也可以用于实现优先级队列，尽管堆是更常用的实现方法。

在有序链表中插入一个数据项的Java代码

        为了在一个有序链表中插入数据项，算法必须首先搜索链表，直到找合适位置：它恰好在第一个比它大的数据项的前面。

        当算法找到了要插入的位置，用通常的方式插入数据项；把新链结点的next字段指向下一个链结点，然后把前一个链结点的next字段改为指向新的链结点。然而，需要kao虑一些特殊情况：链结点可能在表头，或者插在表尾。

public void insert(long j){
    Link newlink = new Link(j);        //make new link
    Link previous = null;              //start at first
    Link current = first;
                                       //until end of list
    while(current!=null && j >current.dData)
    {                                  //or key > current
        previous = current;
        current = current.next;        //go to next item
    }
    if(previous==null)                 //at beginning of list
        first = newlink;               //first --> newLink
    else
        previous.next = newlink;       //old prev -->newLink
    newlink.next = current;            //newLink --> old current
}        //end insert()

        在链表上移动，需要一个previous引用，这样才能把前一个链结点next字段指向新的链结点。创建新链结点后，把current变量设为first，准备搜索正确的插入点。这时也把previous设为null值，这部操作，很重要，因为后面要用这个null值判断是否仍在表头。

package com.list.sortedlist;
public class Sortedlist {
    private Link first;
    public Sortedlist(){
        first = null;
    }
    public boolean isEmpty(){
        return first == null;
    }
    public void insert(long key){
        Link newlink = new Link(key);
        Link previous = null;
        Link current = first;
        while(current!=null && key<current.dData){
            previous = current;
            current = current.next;
        }
        if(previous==null){
            first = newlink;
        }else{
            previous.next = newlink;
        }
        newlink.next = current;
    }
    public Link remove(){
        Link temp = first;
        first = first.next;
        return temp;
    }
    public void displayList(){
        System.out.print("List(first -- >): ");
        Link current = first;
        while(current!=null){
            current.displayLink();
            current = current.next;
        }
        System.out.println("");
    }
}
class Link{
    public long dData;
    public Link next;
    public Link(long dd){
        dData = dd;
    }
    public void displayLink(){
        System.out.print(dData+" ");
    }
}

public static void main(String[] args) {
    Sortedlist theSortedlist = new Sortedlist();
    theSortedlist.insert(20);
    theSortedlist.insert(40);
    
    theSortedlist.displayList();
    
    theSortedlist.insert(10);
    theSortedlist.insert(30);
    theSortedlist.insert(50);
    
    theSortedlist.displayList();
    theSortedlist.remove();
    
    theSortedlist.displayList();
}
//输出：
List(first -- >): 40 20 
List(first -- >): 50 40 30 20 10 
List(first -- >): 40 30 20 10

有序链表的效率

在有序链表插入和删除某一项最多需要O(N)次比较（平均N/2），因为必须沿着链表上一步一步走才能找到正确的位置。然而，可以在O(1)的时间内找到或删除最小值，因为它总在表头。如果一个应用频繁地取最小值项，且不需要快速的插入，那么有序链表是一个有效的方法选择。例如，优先级队列可以用有序链表来实现。

表插入排序

        有序链表可以用于一种高效的排序机制。假设有一个无序数组。如果从这个数组中取出数据，然后一个一个地插入有序链表，它们自动地按顺序排列。把它们从有序列表中删除，重新放入数组，呢么数组就会排序好了。

        这种排序方式总体上比在数组中用常用的插入排序效率更高一些，这是因为这种方式进行的复制次数少一些，它仍然是一个时间级为O(N²)的过程，因为在有序链表中每插入一个新的链结点，平均要与一半已存在数据进行比较，如果插入N个新数据，就进行了N²/4次比较。每一链结点只要进行两次复制：一次从数组到列表，一次从链表到数组。在数组中进行插入排序需要N²次移动，相比之下，2*N次移动更好。

package redis.list.listinsertionsort;

pubic class Link{
    public long dData;
    public Link next;
    public Link(long dd){
    dData = dd;
    }
}
pubic class SortedList{
    private Link first;
    {
    first = null;
    }
    public SortedList(Link[] linkArr){
        first = null;
        for (int i = 0; i < linkArr.length; i++) {
            insert(linkArr[i]);
        }
    }
    public void insert(Link k){
        Link previous = null;
        Link current = first;
        while(current!=null && k.dData>current.dData){
            previous = current;
            current = current.next;
        }
        if(previous==null)
            first = k;
        else
            previous.next = k;
        k.next = current;
    }
    public Link remove(){
        Link temp = first;
        first = first.next;
        return temp;
    }
}

public static void main(String[] args) {
    int size = 10;
    Link[] linkArray = new Link[size];
    for (int i = 0; i < size; i++) {
        int n = (int)(java.lang.Math.random()*99);
        Link newlink = new Link(n);
        linkArray[i] = newlink;
    }
    System.out.print("Unsorted array:");
    for (int i = 0; i < size; i++) {
        System.out.print(linkArray[i].dData+" ");
    }
    System.out.println("");
    SortedList theSortedList = new SortedList(linkArray);
    for (int i = 0; i < size; i++) {
        linkArray[i] = theSortedList.remove();
    }
    System.out.print("Sorted array:");
    for (int i = 0; i < size; i++) {
        System.out.print(linkArray[i].dData+" ");
    }
    System.out.println("");
}
//输出：
Unsorted array:53 36 0 91 37 48 2 20 2 34 
Sorted array:  0 2 2 20 34 36 37 48 53 91

            SortedList类的新构造函数把Link对象数组作为参数读入，然后把整个数组内容插入到新创建的链表中。这样做以后，有助于简化客户（mian（）方法）的工作。

        和基于数组的插入排序相比，表插入排序有一个缺点，就是它要开辟差不多两倍的空间；数组和链表必须同时在内存中存在。但如果有现成的有序链表类可用，那么用表插入排序对不太大的数组排序是比较便利的。

双向链表

        双向链表（不是双端链表），双向链表有什么优点呢？传统链表的一个潜在问题是沿链表的反向遍历是困难。用这样一个语句：

        current = current.next;

        可以很方便地到达下一个链结点然而没有对应的方法回到前一个链结点。根据应用的不同，这个限制可能会引起问题。

        双向链表提供了回头方向走一步的操作能力。即允许向前遍历，也允许向后遍历整个链表。其中秘密在于每个链结点有两个指向其他链结点的引用，而不是一个。第一个像普通链表一样指向下一个链结点。第二个指向前一个链结点。

在双向链表中，Link类定义的开头是这样声明的：

class Link{
    public long dData;        //data item
    public Link next;         //next link in list
    public Link previous;     //previous link in list
}

        双向链表的缺点是每次插入或删除一个链结点的时候，要处理四个链结点的引用，而不是两个：

        两个连接前一个的链结点，两个连接后一个链结点。当然，由于多了两个引用，链结点的占用空间也变大了一点。当然，由于多了两个引用，链结点的占用空间也变大了一点。

         双向链表不必是双端链表（保持一个链表最后一个元素的引用），但这种方式是有用的，所以在后面的例子中将包含双端的性质。

package com.list.doublylinked;
public class DoublyLinked {
}
class Link{
    public long dData;
    public Link next;
    public Link previous;
    public Link(long d){
        dData = d;
    }
    public void displayLink(){
        System.out.print(dData+" ");
    }
}
class DoublyLinkedList{
    private Link first;
    private Link last;
    public DoublyLinkedList(){
        first = null;
        last = null;
    }
    public boolean isEmpty(){
        return first == null;
    }
    public void insertFirst(long dd){
        Link newLink = new Link(dd);
        if(isEmpty()){
            last = newLink;
        }else{
            first.previous = newLink;
        }
        newLink.next = first;
        first = newLink;
    }
    
    public void insertLast(long dd){
        Link newLink = new Link(dd);
        if(isEmpty()){
            first = newLink;
        }else{
            last.next = newLink;
            newLink.previous = last;
        }
        last = newLink;
    }
    
    public Link deleteFirst(){
        Link temp = first;
        if(first.next==null){
            last = null;
        }else{
            first.next.previous = null;
        }
        first = first.next;
        return temp;
    }
    
    public Link deleteLast(){
        Link temp = last;
        if(last.previous==null){
            first = null;
        }else{
            last.previous.next = null;
        }
        last  = last.previous;
        return temp;
    }
    
    public boolean insertAfter(long key,long dd){
        Link current = first;
        while(current.dData!=key){
            current = current.next;
            if(current==null){
                return false;
            }
        }
        Link newlink = new Link(dd);
        if(current==last){
            newlink.next = null;
            last = newlink;
        }else{
            newlink.next = current.next;
            current.next.previous = newlink;
        }
        newlink.previous = current;
        current.next = newlink;
        return true;
    }
    
    public Link deleteKey(long key){
        Link current = first;
        while(current.dData!=key){
            current = current.next;
            if(current==null){
                return null;
            }
        }
        if(current==first){
            first = current.next;
        }else{
            current.previous.next=current.next;
        }
        if(current==last){
            last=current.previous;
        }else{
            current.next.previous = current.previous;
        }
        return current;
    }
    
    public void displayForward(){
        System.out.print("List (first --> last): ");
        Link current = first;
        while(current!=null){
            current.displayLink();
            current = current.next;
        }
        System.out.println("");
    }
    
    public void displayBackward(){
        System.out.print("List (last-->first): ");
        Link current = last;
        while(current!=null){
            current.displayLink();
            current = current.previous;
        }
        System.out.println("");
    }
}

	public static void main(String[] args) {
		DoublyLinkedList theList = new DoublyLinkedList();
		theList.insertFirst(22);
		theList.insertFirst(44);
		theList.insertFirst(66);
		
		theList.insertLast(11);
		theList.insertLast(33);
		theList.insertLast(55);
		
		theList.displayForward();
		theList.displayBackward();
		
		theList.deleteFirst();
		theList.deleteLast();
		theList.deleteKey(11);
		
		theList.displayForward();
		
		theList.insertAfter(22, 77);
		theList.insertAfter(33, 88);
		
		theList.displayForward();
		
	}
	
//输出：
List (first --> last): 66 44 22 11 33 55 
List (last-->first): 55 33 11 22 44 66 
List (first --> last): 44 22 33 
List (first --> last): 44 22 77 33 88

基于双向链表的双端队列

        在双端队列中，可以从任何一头插入和删除，双向链表提供了这个能力。

迭代器

    放在链表内部吗？

    迭代器类       

    迭代器类包含对数据结构中数据项的引用，并用来遍历这些结构的对象（有时，在某些Java类中，叫做“枚举器”）。下面是它们最初的定义：

class ListIterator(){
    private Link current;
    ......
}

       

 。。。。。。

小    结

• 链表包含一个linkedList对象和许多Link对象；

• linkedList对象包含一个引用。这个引用通常叫做first，它指向链表的第一个链结点

• 每个Link对象包含数据和一个引用，通常叫做next，它指向链表的下一个链结点。

• next字段为null值意味着链表的结尾

• 在表头插入链结点需要把新连接点的next字段指向原来的第一个链结点，然后发first指向新链结点

• 在表头删除链结点要把first指向frist next

• 为了遍历链表，从first开始，然后从一个链结点到下一个链结点。一旦找到可以显示，删除或其他方式操纵给链结点

• 新链结点可以插在某个特定值的链结点的前面或后面，首先要遍历找到这个链结点

• 双端链表在链表中维护一个指向最后一个链结点的引用，它通常和叫first一样，叫做last

• 双端链表允许在表尾插入数据项。

• 抽象数据类型是一种数据存储类，不涉及它的实现。

• 栈和队列是ADT。它们既可以用数组实现，又可以用链表实现。

• 有序链表中，链结点按照关键值升序（有时是降序）排列。

• 在有序链表中需要O(N)的时间，因为必须找到正确的插入点。最小链结点的删除需要O(1)的时间

• 双向链表中，每个链结点包含对前一个链结点的引用，同时有对后一个链结点的引用。

• 双向链表允许反向遍历，并可以从表尾删除

• 迭代器是一个引用，它被封装在类对象中，这个引用指向关联的链表中的链结点。

• 迭代器方法允许使用者沿链表移动迭代器，并访问当前指示的链结点

• 能用迭代器遍历链表，在选定的链结点（或所有链结点）上执行某些操作。