Tree-based Regression 笔记
Tree-based Regression(树回归) 将数据集切分成很多份易建模的数据, 即构建树, 然后对每个叶节点上的数据集分别拟合线性模型, 从而解决当数据集拥有较多复杂特征或数据集的数据关系非线性时, 无法使用全局线性模型来拟合数据集的问题.
| 优点 | 可以对复杂和非线性的数据建模 |
| 缺点 | 结果不易理解 |
| 适用数据类型 | 数值型, 标称型 |
基础概念
1. 回归树与模型树
对复杂的关系建模, 一种可行的方式是使用树来对预测值分段, 包括分段常数或分段直线, 若叶节点使用的模型是分段常数则称为回归树, 若叶节点使用的模型是线性回归方程, 则称为模型树.
(1). 本文中, 回归数的分段常数, 就是直接取叶子节点上所对应子集的均值做为预测值.
(2). 本文中, 模型村的线性回归方程, 就是基本线性回归函数, 即通过最小二乘法, 对叶子节点上对应的子集计算出回归系数, 当有测试样本进来时, 就通过回归系数计算出预测值.
2. 二元切分法
前面提到的 Decision Tree 中使用的是 ID3 算法, 它不能处理连续型数据, 只能处理离散型数据(因为它在分割时会按某一特征的所有可能取值来切分); 在处理连续型数据时, 可以采用二元切分法, 即如果特征值大于给定值就走左子树, 否则就走右子树.
3. CART(Classification And Regression Trees, 分类回归树)算法
CART 算法类似 ID3算法, 但它可通过二元切分法用于构建二元树并处理离散型或连续型数据的切分; 若使用不同的叶节点生成函数及误差准则, 就可以构建回归树和模型树.
4. pruning(剪枝)
通过降低决策树的复杂度来避免过拟合的过程称为剪枝.
5. prepruning(预剪枝)
通过设定提前终止条件来减少树节点. (代码 96, 102 行)
预剪枝需要用户指定参数, 这些参数对误差较敏感, 不容易设定.
6. postpruning(后剪枝)
在树构建好后, 通过测试集来在不提高误差的前提下尽可能的合并叶节点.
后剪枝无需用户指定参数.
算法描述
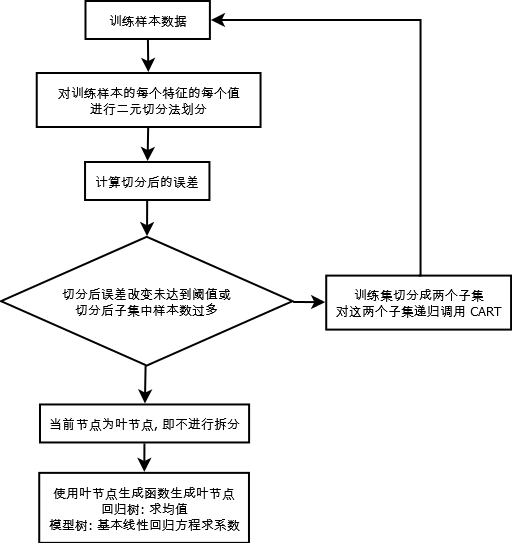
1. CART 算法
(1). 对训练集的每个特征(列)上的每个特征值, 都将数据集切分成两份 (代码 86 行)
(2). 计算切分后的误差 (代码 88 行)
(3). 若切分后的误差改变不大, 或切分后的子集中样本数过多, 则不进行切分 (代码 96, 102 行)
(4). 返回具有最小误差的切分的特征和阈值
(5). 此数法根据误差的计算函数不同及叶节点生成函数不同, 可分为回归树和模型树 (代码 71 行的参数 leafType 和 errType)
2. 后剪枝
(1). 基于已有树切分测试数据
(2). 如果当前树是叶子节点, 则返回
(3). 对树左右子集递归进行后剪枝
(4). 如果剪枝后左右节点皆为叶节点, 则尝试合并两个叶节点
(5). 计算两个叶节点合并前后误差
(6). 若合并后误差降低, 则合并, 否则不合并
代码
# -*- coding: utf-8 -*
from numpy import *
# 加载数据, 数据以 tab 进行分隔
def loadDataSet(fileName): #general function to parse tab -delimited floats
dataMat = [] # 最后一行为分类标签
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = map(float,curLine) # 将每行的数据映射成浮点数
dataMat.append(fltLine)
return dataMat
# 切分数据集
# 将 dataSet 中的数据的第 feature 列, 按 value 值切分成两部分
def binSplitDataSet(dataSet, feature, value):
mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:][0]
mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:][0]
return mat0,mat1
# 叶节点生成函数(回归树)
# 求目标变量的均值, 即对回归树, 叶节点直接设置为常数值(均值)
def regLeaf(dataSet):
return mean(dataSet[:,-1])
# 误差估计函数(回归树)
# var 是均方差函数
def regErr(dataSet):
return var(dataSet[:,-1]) * shape(dataSet)[0]
# 标准线性回归函数
def linearSolve(dataSet):
m,n = shape(dataSet)
X = mat(ones((m,n)));
Y = mat(ones((m,1))) # create a copy of data with 1 in 0th postion
X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1] # and strip out Y
# det 求行列式, 为 0 表示不可逆
xTx = X.T*X
if linalg.det(xTx) == 0.0:
raise NameError('This matrix is singular, cannot do inverse,\n\
try increasing the second value of ops')
# .I 表示求逆
ws = xTx.I * (X.T * Y)
return ws,X,Y
# 叶节点生成函数(模型树)
# 返回标准线性回归函数计算到的系数
# 即对于叶节点, 不再返回一个常数(均值), 而是返回回归函数的系数
def modelLeaf(dataSet):
ws,X,Y = linearSolve(dataSet)
return ws
# 误差估计函数(模型树)
def modelErr(dataSet):
ws,X,Y = linearSolve(dataSet)
yHat = X * ws
return sum(power(Y - yHat,2))
# 寻找数据集上最佳二元切分方式
# 1. 参数 leafType 是对创建叶节点的函数的引用(类似C++中的函数指针)
# 当某个节点不再进行拆分时, 这个节点就会作为叶节点, 需 leafType 来创建出此叶节点
# 2. 参数 errType 是总方差计算函数的引用
# 3. 函数按每个特征的每个特征值将数据集切成两份, 取最小误差的切分方式进行返回
# 4. 返回值的第一个是待拆分的列下标(特征), 第二个是待待分的特征值(拆分成两部分)
def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
# tolS 表示容许的误差下降值, tolN 表示切分的样本数
tolS = ops[0]; tolN = ops[1]
# 如果所有值(最后一列即为特征)相等, 说明无需再划分
if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #exit cond 1
return None, leafType(dataSet)
m,n = shape(dataSet)
S = errType(dataSet)
bestS = inf; bestIndex = 0; bestValue = 0
# 对每个特征(列)的每个取值都尝试拆分, 取误差最小的为切分方式
for featIndex in range(n-1):
for splitVal in set(dataSet[:,featIndex]):
mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): continue
newS = errType(mat0) + errType(mat1)
if newS < bestS:
bestIndex = featIndex
bestValue = splitVal
bestS = newS
# 如果拆分后的误差下降值小于设定阀值, 则不进行拆分
# 因为拆分也误差改变也不大, 还不如不拆分
if (S - bestS) < tolS:
return None, leafType(dataSet) #exit cond 2
# 如果拆分后某个子集中的样本数小于阀值, 则不进行拆分
# 这样可以避免拆分成过于小的子集
mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): #exit cond 3
return None, leafType(dataSet)
# 返回最佳拆分特征(列), 及拆分特征值
return bestIndex,bestValue
# 递归创建树
# 根据 chooseBestSplit 得到最佳拆分的特征(列) 和 特征值, 拆分成两部分
# 在这两部分上再分别递归创建树
def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
if feat == None: return val # 终止条件
retTree = {}
retTree['spInd'] = feat
retTree['spVal'] = val
# 拆分为两份
lSet, rSet = binSplitDataSet(dataSet, feat, val)
# 在两份上分别创建树
retTree['left'] = createTree(lSet, leafType, errType, ops)
retTree['right'] = createTree(rSet, leafType, errType, ops)
return retTree
# 判为是否为树
# 如果返回值为 否, 则为叶子节点
def isTree(obj):
return (type(obj).__name__=='dict')
# 递回树的平均值
# 递归遍历左右子树, 并计算其平均值
def getMean(tree):
if isTree(tree['right']): tree['right'] = getMean(tree['right'])
if isTree(tree['left']): tree['left'] = getMean(tree['left'])
return (tree['left']+tree['right'])/2.0
# 后剪枝函数
# 1. 参数为待剪枝的树和测试数据集
# 2. 剪枝即为合并叶子点, 具体做法就是比较合并前后的误差,
# 如果合并后的误差比合并前的误差小, 就合并, 否则不合并
def prune(tree, testData):
# 如测试集为空, 则返回树的平均值
if shape(testData)[0] == 0: return getMean(tree)
# 拆分测试数据集, 按左,右子树递归进行剪枝
if (isTree(tree['right']) or isTree(tree['left'])):
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet)
# 如果剪枝后左右子树都为叶子节点, 则尝试合并这两个节点
if not isTree(tree['left']) and not isTree(tree['right']):
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\
sum(power(rSet[:,-1] - tree['right'],2))
treeMean = (tree['left']+tree['right'])/2.0
errorMerge = sum(power(testData[:,-1] - treeMean,2))
# 比较合并前后的误差, 若合并后误差更小, 就合并, 否则不合并
if errorMerge < errorNoMerge:
print "merging"
return treeMean
else: return tree
else: return tree
# 对回归树进行预测时的格式化处理函数
# 即走到叶子节点后, 该怎么处理叶子节点上的数据集, 并得到返回值
def regTreeEval(model, inDat):
return float(model)
# 对模型树进行预测时的格式化处理函数
# 即走到叶子节点后, 该怎么处理叶子节点上的数据集, 并得到返回值
def modelTreeEval(model, inDat):
n = shape(inDat)[1]
X = mat(ones((1,n+1)))
X[:,1:n+1]=inDat
return float(X*model)
# 预测函数
# 类似二叉树递归遍历, 走到叶子节点后,
# 就调用 modelEvel 处理叶子节点, 得到的返回值即为预测值
def treeForeCast(tree, inData, modelEval=regTreeEval):
if not isTree(tree): return modelEval(tree, inData)
if inData[tree['spInd']] > tree['spVal']:
if isTree(tree['left']):
return treeForeCast(tree['left'], inData, modelEval)
else:
return modelEval(tree['left'], inData)
else:
if isTree(tree['right']):
return treeForeCast(tree['right'], inData, modelEval)
else:
return modelEval(tree['right'], inData)
# 对测试样本中的每一行调用预测函数
def createForeCast(tree, testData, modelEval=regTreeEval):
m=len(testData)
yHat = mat(zeros((m,1)))
for i in range(m):
yHat[i,0] = treeForeCast(tree, mat(testData[i]), modelEval)
return yHat
if __name__ == "__main__":
# 加载 训练数据 和 测试数据
trainMat = mat(loadDataSet('bikeSpeedVsIq_train.txt'))
testMat = mat(loadDataSet('bikeSpeedVsIq_test.txt'))
# 测试 回归树
myTree = createTree(trainMat, ops=(1,20))
yHat = createForeCast(myTree, testMat[:,0])
print "回归树:", corrcoef(yHat, testMat[:,1],rowvar=0)[0,1]
# 测试 模型树
myTree = createTree(trainMat, modelLeaf, modelErr,(1,20))
yHat = createForeCast(myTree, testMat[:,0], modelTreeEval)
print "模型树:", corrcoef(yHat, testMat[:,1],rowvar=0)[0,1]
# 测试 标准线性回归
ws, X, Y = linearSolve(trainMat)
for i in range(shape(testMat)[0]):
yHat[i] = testMat[i, 0] * ws[1, 0] + ws[0, 0]
print "标准线性回归:", corrcoef(yHat, testMat[:,1],rowvar=0)[0,1]
待补充
1. Tkinter
说明
本文为《Machine Leaning in Action》第九章(Tree-based Regression)读书笔记, 代码稍作修改及注释.
好文参考
1.《CART算法简介》
2.《CART算法学习及实现》