二叉树的基本操作（C）

实现二叉树的创建（先序）、递归及非递归的先、中、后序遍历

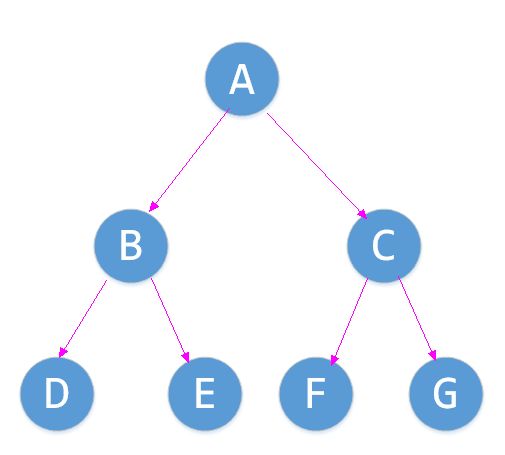
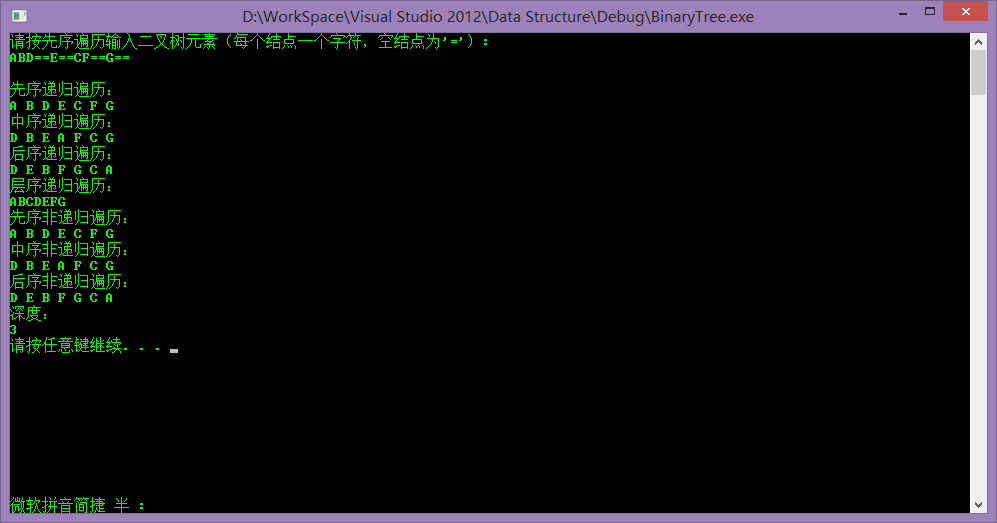
请按先序遍历输入二叉树元素（每个结点一个字符，空结点为'='）:
ABD==E==CF==G==

先序递归遍历：
A B D E C F G
中序递归遍历：
D B E A F C G
后序递归遍历：
D E B F G C A
层序递归遍历：
ABCDEFG
先序非递归遍历：
A B D E C F G
中序非递归遍历：
D B E A F C G
后序非递归遍历：
D E B F G C A
深度：
3
请按任意键继续. . .

 

  1 #include<stdio.h>
  2 #include<stdlib.h>
  3 
  4 #define OK 1
  5 #define ERROR 0
  6 #define TRUE 1
  7 #define FALSE 0
  8 #define OVERFLOW -1
  9 
 10 #define STACK_INIT_SIZE 100
 11 #define STACKINCREMENT 10
 12 
 13 typedef int Status;
 14 
 15 typedef char ElemType;
 16 typedef struct BTNode
 17 {
 18     ElemType data;
 19     struct BTNode *leftChild;
 20     struct BTNode *rightChild;
 21 }BTNode, *BinTree;
 22 
 23 typedef BinTree SElemType;
 24 
 25 typedef struct{//栈结构定义
 26     SElemType *base;
 27     SElemType *top;
 28     int stacksize;
 29 }SqStack;
 30 
 31 BinTree CreateBinTree(BinTree T);
 32 Status Visit(ElemType e);
 33 Status Depth(BinTree T);
 34 Status PreOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 35 Status InOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 36 Status PostOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 37 Status LevelOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 38 
 39 //定义栈的相关操作
 40 Status InitStack(SqStack *S);
 41 Status DestroyStack(SqStack *S);
 42 Status ClearStack(SqStack *S);
 43 Status StackEmpty(SqStack S);
 44 int StackLength(SqStack S);
 45 Status GetTop(SqStack S,SElemType *e);
 46 Status Push(SqStack *S,SElemType e);
 47 Status Pop(SqStack *S,SElemType *e);
 48 Status StackTraverse(const SqStack *S);
 49 
 50 Status PreOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 51 Status InOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 52 Status PostOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));
 53 
 54 int main()
 55 {
 56     int depth;
 57     BinTree Tree = NULL;
 58     Status(*visit)(ElemType e) = Visit;  
 59     printf_s("请按先序遍历输入二叉树元素（每个结点一个字符，空结点为'='）:\n");  
 60     Tree = CreateBinTree(Tree);
 61 
 62     printf_s("\n先序递归遍历：\n");
 63     PreOrderRecursionTraverse(Tree,visit);
 64     printf_s("\n中序递归遍历：\n");
 65     InOrderRecursionTraverse(Tree,visit);
 66     printf_s("\n后序递归遍历：\n");
 67     PostOrderRecursionTraverse(Tree,visit);
 68     printf_s("\n层序递归遍历：\n");
 69     LevelOrderRecursionTraverse(Tree,visit);
 70 
 71     printf_s("\n先序非递归遍历：\n");
 72     PreOrderNoneRecursionTraverse(Tree,visit);
 73     printf_s("\n中序非递归遍历：\n");
 74     InOrderNoneRecursionTraverse(Tree,visit);
 75     printf_s("\n后序非递归遍历：\n");
 76     PostOrderNoneRecursionTraverse(Tree,visit);
 77 
 78     printf_s("\n深度：\n");
 79     depth = Depth(Tree);
 80     printf_s("%d\n", depth);
 81     system("pause");
 82     return 0; 
 83 }
 84 
 85 //创建二叉树
 86 BinTree CreateBinTree(BinTree T)
 87 {
 88     char ch;
 89     scanf_s("%c", &ch);
 90     if (ch == '=')
 91     {
 92         T = NULL;
 93     }
 94     else
 95     {
 96         if (!(T=(BTNode *) malloc(sizeof(BTNode))))
 97         {
 98             exit(OVERFLOW);
 99         }
100         T->data = ch;    //生成根结点
101         T->leftChild = CreateBinTree(T->leftChild);
102         T->rightChild = CreateBinTree(T->rightChild);
103     }
104     return T;
105 }
106 
107 //访问二叉树
108 Status Visit(ElemType e)
109 {
110     if (e == '\0')
111     {
112         return ERROR;
113     }
114     else
115     {
116         printf_s("%c ", e);
117     }
118     return OK;
119 }
120 
121 //先序遍历递归算法
122 Status PreOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
123 {
124     if (T)
125     {
126         if (!Visit(T->data))
127         {
128             return ERROR;
129         }
130         PreOrderRecursionTraverse(T->leftChild, Visit);
131         PreOrderRecursionTraverse(T->rightChild, Visit);
132     }
133     return OK;
134 }
135 
136 //中序遍历递归算法
137 Status InOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
138 {
139     if (T)
140     {
141         InOrderRecursionTraverse(T->leftChild, Visit);
142         if (!Visit(T->data))
143         {
144             return ERROR;
145         }
146         InOrderRecursionTraverse(T->rightChild, Visit);
147     }
148     return OK;
149 }
150 
151 //后序遍历递归算法
152 Status PostOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
153 {
154     if (T)
155     {
156         PostOrderRecursionTraverse(T->leftChild, Visit);
157         PostOrderRecursionTraverse(T->rightChild, Visit);
158         if (!Visit(T->data))
159         {
160             return ERROR;
161         }
162     }
163     return OK;
164 }
165 
166 //层序遍历递归算法
167 Status LevelOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
168 {
169     if (T)
170     {
171         BTNode *Q[100];//假设不溢出
172         int front = -1,rear = -1;
173         if (T)
174         {
175             Q[++rear] = T;
176             printf_s("%c", T->data);
177             while (front != rear)
178             {
179                 BTNode *p;
180                 if (!(p = (BTNode *)malloc(sizeof(BTNode))))
181                 {
182                     exit(OVERFLOW);
183                 }
184                 p = Q[++front];
185                 if (p->leftChild)
186                 {
187                     Q[++rear] = p->leftChild;
188                     printf("%c",p->leftChild->data);
189                 }
190                 if (p->rightChild)
191                 {
192                     Q[++rear] = p->rightChild;
193                     printf("%c",p->rightChild->data);
194                 }
195             }
196         }
197     }
198     return OK;
199 }
200 
201 Status Depth(BinTree T)
202 {
203     int a,b;
204     if (!T)
205     {
206         return ERROR;
207     }
208     else
209     {
210         a = Depth(T->leftChild) + 1;
211         b = Depth(T->rightChild) + 1;
212         return a > b ? a : b;
213     }
214 }
215 
216 //先序遍历非递归算法
217 Status PreOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
218 {
219     SqStack S;
220     SElemType p;
221 
222     InitStack(&S);
223     Push(&S, T);
224 
225     while (!StackEmpty(S))
226     {
227         Pop(&S, &p);
228         if (!Visit(p->data))
229         {
230             return ERROR;
231         }
232         if (p->leftChild)
233         {
234             Push(&S, p->rightChild);
235         }
236         if (p->rightChild)
237         {
238             Push(&S, p->leftChild);
239         }
240     }
241     DestroyStack(&S);
242     return OK;
243 }
244 
245 //中序遍历非递归算法
246 Status InOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
247 {
248     SqStack S;
249     SElemType p;
250 
251     InitStack(&S);
252     Push(&S, T);
253     while (!StackEmpty(S))
254     {
255         while (GetTop(S,&p) && p)
256         {
257             Push(&S, p->leftChild);
258         }
259         Pop(&S, &p);
260         if (!StackEmpty(S))
261         {
262             Pop(&S, &p);
263             if (!Visit(p->data))
264             {
265                 return ERROR;
266             }
267             Push(&S, p->rightChild);
268         }
269     }
270     DestroyStack(&S);
271     return OK;
272 }
273 
274 //后序便利非递归算法
275 Status PostOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))
276 {
277     SqStack S;
278     SElemType p, q;
279     InitStack(&S);
280     Push(&S,T);
281     while(!StackEmpty(S))
282     {
283         while(GetTop(S,&p)&&p&&(p->leftChild||p->rightChild))
284         {
285             Push(&S,p->rightChild);
286             Push(&S,p->leftChild);
287         }
288         if(!StackEmpty(S)){
289             Pop(&S,&p);
290             if (p)
291             {
292                 if(!Visit(p->data))
293                 {
294                     return ERROR;
295                 }
296             }
297             else
298             {
299                 Pop(&S,&p);
300                 if(!Visit(p->data))
301                 {
302                     return ERROR;
303                 }
304             }            
305             while (GetTop(S,&q)&&q&&p==q->rightChild)
306             {
307                 Pop(&S,&p);
308                 if(!Visit(p->data))
309                 {
310                     return ERROR;
311                 }
312                 GetTop(S,&q);
313             }
314         }
315     }
316     DestroyStack(&S);
317     return OK;
318 }
319 
320 //-----------栈的相关操作--------------//
321 Status InitStack(SqStack *S){
322     S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
323     if(!S->base)
324     {
325         exit(0);
326     }
327     S->top = S->base;
328     S->stacksize = STACK_INIT_SIZE;
329     return OK;
330 }
331 
332 Status DestroyStack(SqStack *S){
333     if(!S)
334     {
335         exit(0);
336     }
337     free(S->base);
338     return OK;
339 }
340 
341 Status ClearStack(SqStack *S){
342     if(!S)
343     {
344         return FALSE;
345     }
346     S->top = S->base;
347     return OK;
348 }
349 
350 Status StackEmpty(SqStack S){
351     if(S.top==S.base)
352     {
353         return TRUE;
354     }
355     else
356     {
357         return FALSE;
358     }
359 }
360 
361 int StackLength(SqStack S){
362     return S.stacksize;
363 }
364 
365 Status GetTop(SqStack S,SElemType *e){
366     if(S.top == S.base)
367     {
368         return FALSE;
369     }
370     else
371     {
372         *e = *(S.top-1);
373         return OK;
374     }
375 }
376 
377 Status Push(SqStack *S,SElemType e){
378     if(S->top-S->base>=S->stacksize)
379     {
380         S->base = (SElemType *)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(SElemType));
381         if(!S->base)
382         {
383             exit(0);
384         }
385         S->top = S->base+S->stacksize;
386         S->stacksize += STACKINCREMENT;
387     }
388     *S->top++ = e;
389     return OK;
390 }
391 
392 Status Pop(SqStack *S,SElemType *e){
393     if(S->top==S->base)
394     {
395         return ERROR;
396     }
397     *e = *(--S->top);
398     return OK;
399 }

运行示例