算法系列-有向图遍历

有向图基本算法 -- 遍历算法

1. 图的表示

2. 有向图的遍历算法:深度优先

3. 有向图的遍历算法:广度优先

4 代码反思

5. 下载 

1. 图的表示  

1.1 图的定义

图G定义为V和E的集合G={V, E}，其中V表示图中的所有的顶点集合，E表示的是G中的所有的边的集合。图按照E中的元素是否有方向，分为有向图和无向图。 

1.2 图的表示方法

上面给出的数学上图的定义，那么在计算机中如何表示图？通常意义上，有下面的两种方法：邻接表和邻接矩阵表示法。

无向图的邻接表和邻接矩阵表示如下所示：

 

有向图的邻接表和邻接矩阵表示如下所示：

 

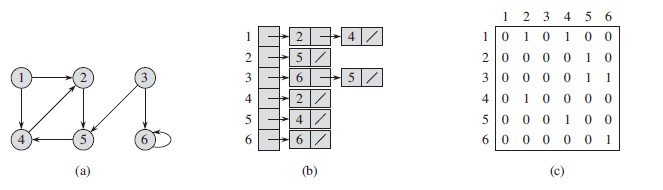
根据上面的表示方法，下面定义图G的这种数据结构（邻接表），首先定义图的顶点GraphVertex：

// 顶点显示的符号

        public char Symbol { get; set; }

        

        // 顶点当前颜色

        public VertexColor Color { get; set; }

        

        // 顶点和开始节点之间的距离

        public int Distance { get; set; }

        

        // 广度遍历父节点

        public GraphVertex Parent { get; set; }

        

        // 深度优先搜索中的开始时间

        public int StartTime { get; set; }

        

        // 深度优先搜索中的结束时间

        public int FinishTime { get; set; }

 

        // 顶点对应的边

        public List<GraphEdge> FollowEdges { get; set; } 

定义图G的边的数据结构：

  // 边开始顶点，在邻接表的存储中其实没有必要存储

        public GraphVertex From { get; set; }

        // 结束顶点

        public GraphVertex To { get; set; } 

        // 边权重

        public int Weight { get; set; } 

定义图：

// 数据成员，这里假设的是顶点的symbol是各个不相同的

        private Hashtable graph = 

            new Hashtable();

        private int time = 0; 

整体上的结构如下：

 

2. 有向图的深度优先算法 

2.1 基本算法

其中d表明的是某个节点第一次被发现的时间点，f表明从节点出发的全部节点已经被发现的时间。  

 

2.2 设计实现 

  // 深度优先遍历算法

        public void DepthFirstVisit(GraphVertex v)

        {

            // 刚刚被发现，颜色为gray

            Console.WriteLine(v.Symbol);

            v.Color = VertexColor.GRAY;

            this.time++;

            // 开始时间

            v.StartTime = this.time;

 

            foreach (GraphEdge edge in v.FollowEdges)

            {

                // 还未被发现

                if (edge.To.Color == VertexColor.WHITE)

                {

                    edge.To.Parent = v;

                    DepthFirstVisit(edge.To);

                }

            }

            

            // 如果边都已经发现完成

            v.Color = VertexColor.BLACK;

            this.time++;

            v.FinishTime = this.time;

            

        }

 

        public void DepthFirstTravel()

        {

            // 全局时间变量

            this.time = 0;

 

            // 初始化

            GraphVertex v;

            foreach (DictionaryEntry e in this.graph)

            {

                v = (GraphVertex)e.Value;

                v.Color = VertexColor.WHITE;

                v.Parent = null;

            }

 

            // 递归调用

 

            // 队所有的顶点

            foreach (DictionaryEntry e in this.graph)

            {

                v = (GraphVertex)e.Value;

 

                // 顶点为白色

                if (v.Color == VertexColor.WHITE)

                {

                    DepthFirstVisit(v);

                }

            }

        } 

3. 有向图的遍历算法：广度优先 

3.1 基本算法

其中color域表示的是当前某个节点被发现的状态。如果是white表明没有被发现，gray表示当前顶点已经被发现，但是从该节点出发的节点还没有被全部发现。parent域定义的是在搜索算法时父节点。distance域表明的是从节点s到某个发现的节点v的路径距离。

3.2 设计实现 

// 广度优先遍历算法，同时生成广度优先树

        public void BreadthFirstTravel(GraphVertex s)

        {

            // 初始化所有节点

            GraphVertex v;

            foreach (DictionaryEntry e in this.graph)

            {

                v = (GraphVertex)e.Value;

                v.Color = VertexColor.WHITE;

                v.Distance = int.MaxValue;

                v.Parent = null;

            }

 

            // 发现第一个节点

            s.Color = VertexColor.GRAY;

            s.Distance = 0;

            s.Parent = null;

 

            // 初始化队列

            Queue context = 

                new Queue();

            context.Enqueue(s);

 

            // 如果队列不空的话

            while (context.Count != 0)

            {

                // 队首元素出队

                v = context.Dequeue() as GraphVertex;

                Console.WriteLine(v.Symbol);

 

                // 遍历v的节点

                foreach (GraphEdge item in v.FollowEdges)

                {

                    if ( item.To.Color == VertexColor.WHITE)

                    {

                        item.To.Color = VertexColor.GRAY;

                        item.To.Distance = v.Distance + 1;

                        item.To.Parent = v;

 

                        context.Enqueue(item.To);

                    }

                }

 

                v.Color = VertexColor.BLACK;

            }

        } 

4. 代码反思 

上面的搜索代码结构是比较典型的搜索结构：首先定义队列或者是栈来保存程序运行状态，如果容器不空，取出元素，然后对取出的元素做一些处理。 

5. 代码下载 

/Files/xuqiang/DirectedGraph1.rar 

=================================================================

Java版代码实现

import java.util.ArrayList;

import java.util.List;



// 模块E

public class AdjMatrixGraph<E> {

protected SeqList<E> vertexlist; // 顺序表存储图的顶点集合



protected int[][] adjmatrix; // 图的邻接矩阵 二维图 存储的是每个顶点的名称（A,B,C,D....）



private final int MAX_WEIGHT = Integer.MAX_VALUE / 2;



// private final int MAX_WEIGHT = 10000;



// -------一，构造图：增删改查-------------------------//

public AdjMatrixGraph(int n) {// n为顶点的数目

this.vertexlist = new SeqList<E>(n);

this.adjmatrix = new int[n][n];

for (int i = 0; i < n; i++)

for (int j = 0; j < n; j++)

this.adjmatrix[i][j] = (i == j) ? 0 : MAX_WEIGHT;

// 对角线上为0，其他的都为无穷大。

}



// 构造函数内一个是字符串数组，一个是edge的set集合

public AdjMatrixGraph(E[] vertices, Edge[] edges) {

this(vertices.length);

for (int i = 0; i < vertices.length; i++)

insertVertex(vertices[i]);// 添加顶点

for (int j = 0; j < edges.length; j++)

insertEdge(edges[j]);// 添加边

}



// 构造函数内一个是数组集合，一个是edge的set集合

public AdjMatrixGraph(SeqList<E> list, Edge[] edges) {

this(list.length());

this.vertexlist = list;

for (int j = 0; j < edges.length; j++)

insertEdge(edges[j]);

}



// 显示出一共顶点的数目

public int vertexCount() {

return this.vertexlist.length();

}



// 根据编号得到该顶点

public E get(int i) {

return this.vertexlist.get(i);

}



public boolean insertVertex(E vertex) { // 插入一个顶点，若插入成功，返回true



return this.vertexlist.add(vertex);

}



public boolean insertEdge(int i, int j, int weight)

// 插入一条权值为weight的边<vi,vj>，若该边已有，则不插入

{

if (i >= 0 && i < vertexCount() && j >= 0 && j < vertexCount()

&& i != j && adjmatrix[i][j] == MAX_WEIGHT) {

// 先判断该边两个顶点的编号是否在范围，该边的值是否为最大值，来确定所添加边的值是否存在；

this.adjmatrix[i][j] = weight;// 添加权值

return true;

}

return false;

}



public boolean insertEdge(Edge edge) {

if (edge != null)

;

return insertEdge(edge.start, edge.dest, edge.weight);

}



public String toString() {

String str = "顶点集合： " + vertexlist.toString() + "\n";

str += "邻近矩阵：    \n";

int n = vertexCount();

for (int i = 0; i < n; i++) {

for (int j = 0; j < n; j++) {

if (adjmatrix[i][j] == MAX_WEIGHT)

str += " ∞";// 最大值（不存在）的时候的显示方式；

else

str += " " + adjmatrix[i][j];// 每一个顶点到其他顶点的权值

}

str += "\n";

}

return str;

}



public boolean removeEdge(int i, int j) // 删除边〈vi,vj〉，若成功，返回T

{

if (i >= 0 && i < vertexCount() && j >= 0 && j < vertexCount()

&& i != j && this.adjmatrix[i][j] != MAX_WEIGHT) {

// 判断该边的两个顶点是否存在，以及改边的值是否为最大值来判断改边是否存在；

this.adjmatrix[i][j] = MAX_WEIGHT; // 设置该边的权值为无穷大，说明已不存在；

return true;

}

return false;

}



public boolean removeVertex(int v) // 删除序号为v的顶点及其关联的边

{

int n = vertexCount(); // 删除之前的顶点数

if (v >= 0 && v < n) {// V的要求范围

this.vertexlist.remove(v); // 删除顺序表的第i个元素，顶点数已减一

for (int i = v; i < n - 1; i++)

for (int j = 0; j < n; j++)

this.adjmatrix[i][j] = this.adjmatrix[i + 1][j]; // 邻接矩阵：删除点以下往上移动一位

for (int j = v; j < n - 1; j++)

for (int i = 0; i < n - 1; i++)

this.adjmatrix[i][j] = this.adjmatrix[i][j + 1]; // 邻接矩阵：删除点以右往左移动一位

return true;

}

return false;

}



public int getFirstNeighbor(int v) // 返回顶点v的第一个邻接顶点的序号

{

return getNextNeighbor(v, -1);

} // 若不存在第一个邻接顶点，则返回-1



public int getNextNeighbor(int v, int w) { // 返回v在w后的下一个邻接顶点

if (v >= 0 && v < vertexCount() && w >= -1 && w < vertexCount()// 对v

// w的范围限定

&& v != w)

for (int j = w + 1; j < vertexCount(); j++)

// w=-1时，j从0开始寻找下一个邻接顶点

if (adjmatrix[v][j] > 0 && adjmatrix[v][j] < MAX_WEIGHT)

// 遍历和v相关的点，得到下一个点

return j;

return -1;

}



// -------二，最小生成树-------------------------//



/*

* 普里姆算法的基本思想: 取图中任意一个顶点 v 作为生成树的根，之后往生成树上添加新的顶点 w。 在添加的顶点 w

* 和已经在生成树上的顶点v之间必定存在一条边， 并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小。

* 之后继续往生成树上添加顶点，直至生成树上含有 n-1 个顶点为止。

*/



public AdjMatrixGraph minSpanTree_prim() {

Edge[] mst = new Edge[this.vertexCount() - 1]; // n个顶点最小生成树有n-1条边

int un;

List<Integer> u = new ArrayList<Integer>();// 存放所有已访问过的顶点集合

u.add(0);// 起始点默认为标识为0的顶点

for (int i = 0; i < this.vertexCount() - 1; i++) {

int minweight = MAX_WEIGHT;// 最小边的时候，权值

int minstart = MAX_WEIGHT;// 最小边的时候，起点

int mindest = MAX_WEIGHT;// 最小边的时候，终点

for (int j = 0; j < u.size(); j++) {

un = u.get(j);

for (int k = 0; k < this.vertexCount(); k++) {

// 获取最小值的条件：1.该边比当前情况下的最小值小；2.该边还未访问过；

if ((minweight > adjmatrix[un][k]) && (!u.contains(k))) {

minweight = adjmatrix[un][k];

minstart = un;

mindest = k;

}

}

}

System.out.println("一次遍历所添加的最小边：他的权值，起点，终点分别为：weight:" + minweight

+ "start:" + minstart + "dest:" + mindest);

u.add(mindest);

Edge e = new Edge(minstart, mindest, adjmatrix[minstart][mindest]);

mst[i] = e;

}

return new AdjMatrixGraph(this.vertexlist, mst); // 构造最小生成树相应的图对象

}



/*

* public AdjMatrixGraph minSpanTree_kruskal() { }

*/



// -------三，图的遍历（广度遍历，深度遍历）-------------------------//

public void DFStraverse() {

int n = this.vertexCount();

boolean[] visited = new boolean[n];

for (int i = 1; i < n; i++) {

visited[i] = false;

}

// 编号0为起始点，进行一次深度优先遍历（一次得到一个连通分量）

for (int j = 0; j < n; j++) {

if (!visited[j]) {

System.out.println("以该顶点为" + j + "起始点的遍历：");

this.DFS(j, visited);

}

}

}



// 参数1：遍历起始点的编号，参数2：记录各个顶点是否被访问过

public void DFS(int v, boolean[] visited2) {

boolean[] visited = visited2;

visited[v] = true;

System.out.println("遍历顶点" + v);

for (int w = this.getFirstNeighbor(v); w >= 0; w = this

.getNextNeighbor(v, w)) {

if (!visited[w]) {

visited[w] = true;

DFS(w, visited);

}

}

}



public void BFStraverse() {

int n = this.vertexCount();

boolean[] visited = new boolean[n];

MyQueue myqueue = new MyQueue();

for (int i = 1; i < n; i++) {

visited[i] = false;

}



for (int j = 0; j < n; j++) {

if (!visited[j]) {

visited[j] = true;

System.out.println("遍历起点：" + j);

myqueue.EnQueue(j);

while (!myqueue.empty()) {

int v = (Integer) myqueue.DeQueue();

System.out.println("遍历点：" + v);

for (int w = this.getFirstNeighbor(v); w >= 0; w = this

.getNextNeighbor(v, w)) {

if (!visited[w]) {

visited[w] = true;

myqueue.EnQueue(w);

}

}

}

}

}



}



// -------四，图的最短路径Dijkstra算法-------------------------//

public void Dijkstra() {

int n = this.vertexCount();

int minweight = MAX_WEIGHT;

int minUn = 0;

int[] minmatrix = new int[n];// 存放当前起始点到其余各个顶点的距离；

boolean[] isS = new boolean[n];// 判断各个是否被访问过

String[] route = new String[n];// 每个字符串是显示对应顶点最短距离的路径；

for (int i = 1; i < n; i++) {// 初始化

minmatrix[i] = adjmatrix[0][i];

isS[i] = false;

route[i] = "起点->" + i;

}

for (int i = 1; i < n; i++) {

// 选择 当前 和起点 连通的，且值最小的顶点；

for (int k = 1; k < n; k++) {

if (!isS[k]) {

if (minmatrix[k] < minweight) {

minweight = minmatrix[k];

minUn = k;

}

}

}

isS[minUn] = true;// 将该点设置为已访问；

for (int j = 1; j < n; j++) {

if (!isS[j]) {// 判断：该顶点还没加入到S中/属于U-S；

if (minweight + adjmatrix[minUn][j] < minmatrix[j]) {

// 通过当下最小值 访问到得其他顶点的距离小于原先的最小值 则进行交换值

minmatrix[j] = minweight + adjmatrix[minUn][j];

route[j] = route[minUn] + "->" + j;

}

}

}

minweight = MAX_WEIGHT;// 因为要放到下一个循环中，所以一定要重设置一下，回到最大值

}

for (int m = 1; m < n; m++) {

System.out.println("从V0出发到达" + m + "点");

if (minmatrix[m] == MAX_WEIGHT) {

System.out.println("没有到达该点的路径");

} else {

System.out.println("当前从V0出发到达该点的最短距离：" + minmatrix[m]);

System.out.println("当前从V0出发到达该点的最短距离：" + route[m]);



}

}

}



// -------五，图的连通性-------------------------//

public boolean isConnect() {

int n = this.vertexCount();

boolean[] visited = new boolean[n];

// 记录不能一次深度优先遍历通过的数目

// 全部顶点作为出发点开始遍历，如果全部都不能一次遍历通过（notConnectNum == n），说明该图不连通。

int notConnectNum = 0;

for (int j = 0; j < n; j++) {

for (int i = 0; i < n; i++) {

visited[i] = false;

}

this.DFS(j, visited);

for (int k = 0; k < n; k++) {

System.out.println(visited[k]);

if (visited[k] == false) {

notConnectNum++;

break;// 一旦有没有被遍历到的顶点（说明该顶点不属于该连通分量），跳出循环

}

}

}

if (notConnectNum == n) {

System.out.println("此图是不连通的");

return false;

} else {

System.out.println("此图是连通的");

return true;

}

}



// -------六，图的拓扑排序-------------------------//

public void topologicalSort() {

int n = this.vertexCount();

int[] indegree = new int[n];

MyStack mystack = new MyStack();

String route = "拓扑排序出发：";

int count = 0;

for (int i = 0; i < n; i++) {

indegree[i] = 0;

for (int j = 0; j < n; j++) {//获取每一个顶点的入度

if (adjmatrix[j][i] != 0 && adjmatrix[j][i] != MAX_WEIGHT) {

indegree[i] += 1;

}

}//先将入度为0的顶点加入到栈中

if (indegree[i] == 0) {

mystack.push(i);

}

}

while (!mystack.empty()) {

int v = (Integer) mystack.pop();//从栈中删除该顶点

route += "->" + v;

++count;

for (int w = this.getFirstNeighbor(v); w >= 0; w = this

.getNextNeighbor(v, w)) {

indegree[w] -= 1;//因为该顶点被“删除”，所有以该顶点为弧尾的边的弧头的入度减一

if (indegree[w] == 0) {

mystack.push(w);//先将入度为0的顶点加入到栈中

}

}

}

if (count < n) {//当经历拓扑排序遍历后，所有顶点都被“删除”时（count=n），此时实现拓扑排序

System.out.println("存在回路，不满足拓扑排序的条件");

} else {

System.out.println("实现拓扑排序" + route);



}

}


}