支持向量机通俗导论（理解SVM的三层境界）

  作者：July、pluskid；致谢：Wind、白石。
出处：结构之法算法之道blog。（纯属转载

前言

    动笔写这个支持向量机(support vector machine)是费了不少劲和困难的，从5月22日凌晨两点在微博上说我要写了，到此刻真正动笔要写此文，中间竟然隔了近半个月(而后你会发现，我写完此文又再得花半个月，前后加起来，写这个SVM便要花近一个月)。原因很简单，一者这个东西本身就并不好懂，要深入学习和研究下去需花费不少时间和精力，二者这个东西也不好讲清楚，尽管网上已经有不少朋友已经写得不错了(见文末参考链接..)，但在描述数学公式的时候还是显得不够。得益于同学白石的数学证明，我还是想尝试写一下，希望本文在兼顾通俗易懂的基础上，真真正正能足以成为一篇完整概括和介绍支持向量机的导论性的文章。

    本文作为Top 10 Algorithms in Data Mining系列第二篇文章，将主要结合支持向量机导论、数据挖掘导论及网友的Free Mind的支持向量机系列而写(于此，还是一篇读书笔记，只是加入了自己的理解，有任何不妥之处，还望海涵)，宏观上整体认识支持向量机的概念和用处，微观上深究部分定理的来龙去脉，证明及原理细节，力求深入浅出 & 通俗易懂。

    同时，本文，亦即理解SVM分三层境界，

 

• 第一层、了解SVM(你只需要对SVM有个大致的了解，知道它是个什么东西便已足够)；
• 第二层、深入SVM(你将跟我一起深入SVM的内部原理，通宵其各处脉络，以为将来运用它时游刃有余)；
• 第三层、证明SVM(当你了解了所有的原理之后，你会有大笔一挥，尝试证明它的冲动)；

 

    最后谈谈SVM的应用，编码实现及开源工具libsvm，以此逐层深入，从而照顾到水平深浅度不同的读者，在保证浅显直白的基础上尽可能深入，还读者一个明明白白透透彻彻的SVM，希望我能做到。还是那句原话，有任何问题，欢迎任何人随时不吝指正 & 赐教，谢谢。

 

导论、从人工智能到机器学习

    根据支持向量机导论一书的介绍，人工资能领域的研究者们很早就开始研究了学习问题。Alan Turing在1950年就指出了学习器的思想，以反驳Lady Lovelace的“机器只会做我们指挥它们做的事情”，意思是电脑只会执行人们输入给它的指令，不具备任何学习能力。而Turing则评论道：学习器的一个重要特征便是，其施教者对于内部实际的运转过程中在很大程度上的确是无知的，而受教者的行为在一定程度上却是预测的。仅仅在数年后，初始的学习器便被开发了出来，比如Arthur Samuel的跳棋程序便是强化学习的一个早期例子，Frank Rosenblatt的感知机包含了下一章讲讨论的系统的许多特征。特别要指出，把学习问题建模使其成为适当假设空间中的搜索问题便是人工智能方法的特点。

    学习算法的发展使得它本身成为了人工智能的一个重要的子领域，并最终形成了机器学习这样一个独立的学科。而什么是数据挖掘呢？

    数据挖掘是机器学习、数据库和统计学三者结合的产物，数据挖掘首先要确定挖掘的任务或目的，确定了挖掘任务之后，就要决定使用什么样的挖掘算法，选择了算法之后便可以实施数据挖掘操作，获取有用的信息或模式。

    其实，很多时候，分类可以被称之为机器学习领域内的一种学习方法，也可以被称之为数据挖掘领域内的一种算法，两者之间，并不是井水不犯河水。

 

第一层、了解SVM

1.0、什么是支持向量机SVM

    在进入第一层之前，你只需了解什么是支持向量机SVM就够了，而要明白什么是SVM，便得从分类说起。

    分类作为数据挖掘领域中一项非常重要的任务，目前在商业上应用最多(比如分析型CRM里面的客户分类模型，客户流失模型，客户盈利等等，其本质上都属于分类问题)。而分类的目的则是学会一个分类函数或分类模型(或者叫做分类器)，该模型能吧数据库中的数据项映射到给定类别中的某一个，从而可以用于预测未知类别。
    说实话，上面这么介绍分类可能你不一定内心十分清楚。我来举个例子吧，比如心脏病的确诊中，如果我要完全确诊某人得了心脏病，那么我必须要进行一些高级的手段，或者借助一些昂贵的机器，那么若我们没有那些高科技医疗机器怎么办？还怎么判断某人是否得了心脏病呢？

    当然了，古代中医是通过望、闻、问、切“四诊”，但除了这些，我们在现代医学里还是可以利用一些比较容易获得的临床指标进行推断某人是否得了心脏病。如作为一个医生，他可以根据他以往诊断的病例对很多个病人(假设是500个)进行彻底的临床检测之后，已经完全确定了哪些病人具有心脏病，哪些没有，同时，在这个诊断的过程中，医生理所当然的记录了他们的年龄，胆固醇等10多项病人的相关指标。那么，以后，医生可以根据这些临床资料，对后来新来的病人通过检测那10多项年龄、胆固醇等指标，以此就能推断或者判定病人是否有心脏病，虽说不能达到100%的标准，但也能达到80、90%的正确率，而这一根据以往临场病例指标分析来推断新来的病例的技术，即成为分类classification技术。

    其实，若叫分类，可能会有人产生误解，以为凡是分类就是把一些东西或样例按照类别给区分开来，实际上，分类方法是一个机器学习的方法，分类也成为模式识别，或者在概率统计中成为判别分析问题，或许会让人们消除此类误解。

    OK，既然讲到了病例诊断这个例子，接下来咱们就以这个例子来简单分析下SVM。
假定是否患有心脏病与病人的年龄和胆固醇水平密切相关，下表对应10个病人的临床数据(年龄用[x1]表示，胆固醇水平用[x2]表示)：

    这样，问题就变成了一个在二维空间上的分类问题，可以在平面直角坐标系中描述如下：根据病人的两项指标和有无心脏病，把每个病人用一个样本点来表示，有心脏病者用“+”形点表示，无心脏病者用圆形点，如下图所示：

 

    如此我们很明显的看到，是可以在平面上用一条直线把圆点和“+”分开来的。当然，事实上，还有很多线性不可分的情况，下文将会具体描述。

 

    So，本文将要介绍的支持向量机SVM算法便是一种分类方法。

• 所谓支持向量机，顾名思义，分为两个部分了解，一什么是支持向量(简单来说，就是支持 or 支撑平面上把两类类别划分开来的超平面的向量点，下文将具体解释)，二这里的“机”是什么意思。我先来回答第二点：这里的“机（machine,机器）”便是一个算法。在机器学习领域，常把一些算法看做是一个机器，如分类机(当然，也叫做分类器)，而支持向量机本身便是一种监督式学习的方法(什么是监督学习与非监督学习，请参见第一篇)，它广泛的应用于统计分类以及回归分析中。

    对于不想深究SVM原理的同学(比如就只想看看SVM是干嘛的)，那么，了解到这里便足够了，不需上层。而对于那些喜欢深入研究一个东西的同学，甚至究其本质的，咱们则还有很长的一段路要走，万里长征，咱们开始迈第一步吧(相信你能走完)。

1.1、线性分类

    OK，在讲SVM之前，咱们必须先弄清楚一个概念：线性分类器。

 

• 这里我们考虑的是一个两类的分类问题，数据点用  x  来表示，这是一个  n  维向量，而类别用  y  来表示，可以取 1 或者 -1 ，分别代表两个不同的类。一个线性分类器就是要在  n  维的数据空间中找到一个超平面，其方程可以表示为：

   

  wTx+b=0

    但即使我已经给出了线性分类器的定义及公式，相信，仍然是有相当一部分读者是不知所谓的超平面(w，b)中w，和b所指是何物的？但本文尽量不留遗漏，以期尽量将有必要了解的技术细节原原本本的和盘托出，如下：

 

• 上面已经说过，两类问题的分类通常用一个实值函数f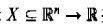：(R^n即指n唯平面)按照这样的方式操作：当f(x)>=0，输入想x=(x1，...xn)‘赋给正类，否则赋给负类，考虑当f(x)，x属于X是线性函数的情况，函数可以写为：f(x)=<w，b> + b。这个式子的几何解释是，<w，x>+b=0所定义的超平面讲输入空间X(各种点)分为两半。
• 也就是说，超平面是维数为n-1的仿射子空间，它将空间分为两部分，这两部分对应输入中两类不同的点，对应着超平面上面的正区域和超平面下面的负区域，当b的值变化时，超平面平行于自身移动，示意图如下(注意体会途中w，b的几何意义，我之前曾以为在实际应用SVM的过程中，所谓调参就是调这里的w，b，而后意识到其实不是如此，而是如Wind所说的，核函数的选择、惩罚因子C的大小，或者比如采用高斯核函数的时候，参数主要是核函数的\gamma变量以及权衡系数C)：

 

• 

1.2、线性分类的一个例子

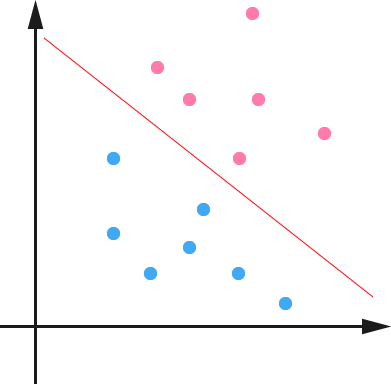
    来理论可能读者看不懂，咱们来直接举一个例子吧，且举最简单的例子，一个二维平面(一个超平面，在二维空间中的例子就是一条直线)，如下图所示，平面上有两种不同的点，分别用两种不同的颜色表示，一种为红颜色的点，另一种则为蓝颜色的点，红颜色的线表示一个可行的超平面。

    从上图中我们可以看出，这条红颜色的线把红颜色的点和蓝颜色的点分开来了。而这条红颜色的线就是我们上面所说的超平面，而现在的情况是，这个所谓的超平面的的确确便把这两种不同颜色的点分隔开来，换句话说，事实上，是存在这样一个超平面可以把两类数据分隔开来的，比如，在超平面一边的数据点所对应的  y  全是 -1 ，而在另一边全是 1 。具体来说，我们可以令  f(x)=wTx+b  ，显然，如果  f(x)=0  ，那么  x  是位于超平面上的点。我们不妨要求对于所有满足  f(x)<0  的点，其对应的  y  等于 -1 ，而  f(x)>0  则对应  y=1  的数据点。

 

• 当然，有些时候（或者说大部分时候）数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在(不过关于如何处理这样的问题我们后面会讲)，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。

 

    更进一步，我们在进行分类的时候，将数据点  x 代入  f(x)  中，如果得到的结果小于 0 ，则赋予其类别 -1 ，如果大于 0 则赋予类别 1 。如果  f(x)=0 ，则很难办了，分到哪一类都不是(后续会说明此种情况)。

(详见附件)

 http://blog.csdn.net/v_july_v/article/details/7624837