如何量化评估被测试软件的质量

如何去量化评估软件的质量，属于发散性的问题，可从多个角度去考虑。其实国际上关于软件质量已有公认的国际标准（ISO/IEC 9126），我国在此基础之上，也形成了我国的国家标准GB/T 16260，二者在内容上非常相似。

ISO/IEC 9126标准中规定，软件的质量可以从以下6个大的特性来衡量：功能性（Functionability）、可靠性（Reliability）、可用性（Usability）、有效性（Efficiency）、可维护性（Maintainability）、可移植性（Portability），每个质量特性还可以细分为很多子特性，如下图

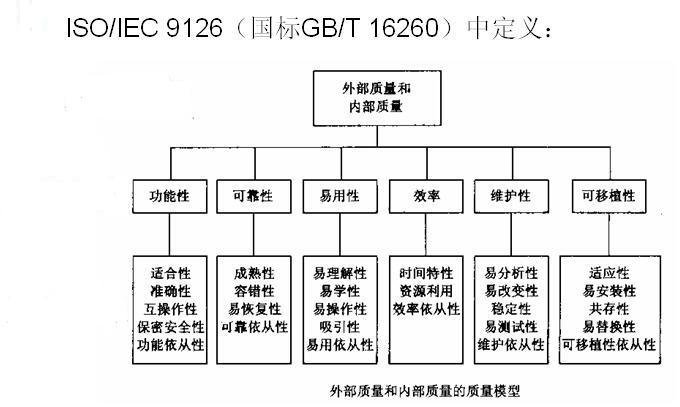
针对本文的问题，可以从各种元数据（即度量元，英文Metrics）分析，得到相应的质量标准。具体到“量化”评估，我只对我所熟悉的部分做简单说明。

1 可维护性：

借助于静态质量度量法，软件的可维护性成为目前“量化”评估最成熟的一个质量特性之一。

×针对的是程序源代码

×主要用于质量评审阶段，即每个模块在版本管理库中形成了“基线”后，各小组对代码的评审

ISO/IEC 9126标准对软件可维护性采用四个分类标准来评估：可分析性、可修改性、稳定性、可测性。

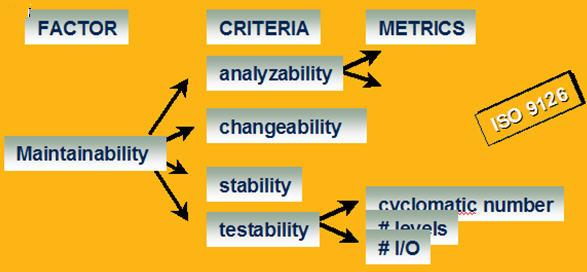
每个分类标准又由一系列度量元组成，每个度量元分配一个权重，由规则的取值与权重值，加权平均计算出每个标准的值。通过质量标准值的大小，可将程序代码的质量分成四个级别，由高到底依次是EXCELLENT（优秀）、GOOD（良好）、FAIR（合格）、POOR（不合格）。其中属于前三个等级的编码遵守或基本遵守了质量标准的要求，属于最后一个等级的编码没有遵守质量标准的要求，需要对其进行修改和完善。举例如下

这个质量标准是评价函数的稳定性的。最上面一行是这个质量标准的计算公式：

function_STABILITY = ic_varpe + ct_exit + dc_calls + ic_param该公式表明，该质量标准由四个度量元所决定，即ic_varpe 、ct_exit、dc_calls、ic_param，每个度量元的权重均为一。该质量标准的最高得分为4分，即当构成该质量标准的四个度量元的值均在我们设定的范围内时，该项质量标准得分为4分，当有三个度量元的值均在我们设定的范围内时，该项质量标准得分为3分，以此类推。最后根据具体的得分，可以判定程序代码在该项质量标准上所处的等级。 最后，综合多个质量标准，得出代码的可维护性质量标准。根据具体的得分，可以判定程序代码在可维护性上所处的等级。

 

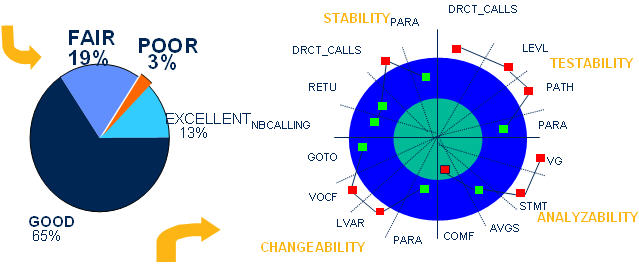
从上面的最终结果可以看出，整个项目中，成绩为“优秀”的达到13%，“良好”的达到65%，“不合格”的为3%。我们借助于ISO/IEC 9126提供的质量模型，可以得出：成绩为“不合格”的3%的函数为整个项目的薄弱点，根据实际情况，这些代码可能需要重写或者在测试活动中重点关注。

以上的方法在实施过程中，如果单靠人工的话，效率会很低。之所以说针对“可维护性”的量化比较成熟，是因为市场上已经有了专门的工具协助，例如Logiscope、Macabe等，可以大大的提高 工作效率。

通过分析软件的可靠性，可以尽早发现程序在编码上的质量薄弱点，从而以比较低的成本使不足得到修改。

2 功能性

功能测试是最基本的测试类型，也是最容易被理解的。但具体到软件功能测试的“量化”，可以借助于BUG的估算。举例子说明：

两个小组独立地测试同一个程序的某一个公共模块，第一组发现25个错误，第二组发现30个错误，在两个小组发现的错误中有15个是共同的，那么根据估算的方法 S = m / (p/n)，估计出该模块中的错误总数是50个，第一组测试的得分为25/50 × 100% = 50%，第二组为30/50 ×100%=60%。把该得分推而广之到程序的 其他部分，从而可以估算出量化的功能测试效果，预估出软件功能测试的结束时间。

在元数据量不大的情况下，该方法具有一定的随机性，不同的人参与可能会得到不同的结果，但随着元数据的逐步积累，该方法得到的结果会更加趋向于真实。

3 可靠性

 关于软件的可靠性方面，据我了解，目前还不是特别成熟，大多都是借鉴硬件可靠性的做法，如，FTA（故障树分析）、FMEA（失效模式与效应分析）等，而且多处于理论研究阶段。

通过分析软件的可靠性，可以评估软件的发布风险。

设错误总数为X，那么甲发现错误的概率P(甲)为    25    /    X，乙发现错误的概率P(乙)为    30    /    X    ，甲乙同时发现错误的概率P(同)为    15    /    X    。   
   因为    P(甲)*P(乙)=P(同)      ，所以(25    /    X)    *    (30    /    X)    =    15    /    X   
   计算而得X=50

 

两个小组独立地测试同一个程序，第一组发现25个错误，第二组发现30个错误，在两个小组发现的错误中有15个是共同的，那么可以估计程序中的错误总数是 ___个。

A．25 B．30 C．50 D．60

    当然，任何一个了解估算方法的朋友都可以根据公式计算出最终的结果是50个，这没有什么问题。――但是，我在这里引用这个题目，是希望我们可以把学习这件事情通过类比变得更加有趣一点。

    其实，如何估算一个系统中存在的缺陷数，我们的老祖宗早就有现成的方法了。不信，请看我在我们老祖宗的数学专著中找到的一个实践问题：“有一口鱼塘，不知道其中有多少条鱼，如何才能估算出池塘中鱼的数量？”（当然，原文不是这样，请原谅我一下子找不到出处，只好凭记忆用我的语言描述一下了）。我们老祖宗给出的答案是这样的：

1. 首先，从鱼塘中打捞出一些鱼（假设数量为m）；
2. 将这些鱼做上记号，然后将其放回鱼塘；
3. 等待一段时间，等到鱼均匀分布在鱼塘中了之后，再次打捞上来一些鱼（假设数量为n）；
4. 统计第二次打捞上来的鱼中的带记号者（假设数量为p）；
5. 计算得出鱼塘中鱼的数量为 S = m / (p/n)

    对这个答案最简单的理解是： 假设第一次做了记号的鱼在鱼塘中是均匀分布的，第二次打捞上来的n条鱼中有p条是有记号的，则说明有记号的鱼的分布密度是p/n，鱼塘中一共有m条有记号的鱼，当然总的鱼数量就是 S = m / (p/n)了 。

    再回到我们的原始问题，很容易做一个类比，第一个小组发现了25个缺陷（相当于第一次打捞的鱼m），第二个小组发现了30个缺陷（相当于第二次打捞上来的鱼n），两者相同的是15个（相当于是p），所以答案是 50。

    所以，从现在开始，不要再认为这个方法是什么深奥的方法――看看，我们的老祖宗都能熟练运用呢

    本来，到这里就可以告一段落了，可是我们能不能再深入点思考这个问题呢？

    这种方法显然是可以得到一个估算结果，但这种方法在哪些情况下不合适，使用时有什么注意事项没有呢？

    还是回过头看我们养鱼的例子，很显然，我们讨论的前提是“做记号的鱼在池塘中分布均匀”，如果这个条件不满足，我们的估算结果显然是有很大的偏差的。就鱼塘来说，不同类型的鱼由于喜欢的食物种类不同，喜欢分布在不同的层次，这样一来的话，在打捞的时候就要注意，如果只侧重在某一个水层，显然结果是有很大的偏差的，另外，由于鱼塘边上的温度相对较低，夏天鱼更加喜欢在鱼塘边休息……，可见，要达到“平均”这样的条件还是有难度的…… ―― 等等，我们讨论了这么久的鱼，和我们的缺陷有什么关系呢？

    别忘了，缺陷在系统中的分布和鱼在鱼塘中的分布可是有异曲同工之妙的哦 。缺陷有不同的类型（功能缺陷，性能缺陷，安全性缺陷……），分布在不同的模块，由于模块设计和实现人员的水平的差异，模块自身复杂度的差异等，不同模块中的缺陷分布显然是不同的，一个系统中，由于测试的测试不同，不同类型缺陷的发现效率也是不同的……――再看看，这和我们的鱼塘是不是一回事？

    关于鱼塘和缺陷的故事，如果我们要深究下去，还会发现他们的很多共同点，当然，你也可以提出各种方法来修正我们这个简单的模型――但这不是我们的重点。 我要说的重点是：无论如何，在这条路上的思考是不是会比简单的背公式更有趣一些呢？