[软考]计划评审技术PERT详细解释及应用，实例讲解收集（信息系统项目管理师-时间管理）

开场白

这是软考文章的第二篇了，主要分析了PERT的计算题，关键点在于记往三个范围并能够画出正态分布图，各种变形题就基本可以解决了。

文章由简入繁，由浅入深，再加上自己的理解，其中难免有纰漏，若路过此处的同行发现错误或有更好的解题思路，请不吝赐教。

计划评审技术PERT(Program Evaluation and Review Technique)就是把工程项目当成一种系统，用网络图或者表格或者矩阵来表示各项具体工作的先后顺序和相互关系，以时间为中心，找出从开工到完工所需要时间的最长路线，并围绕关键路线对对系统进行统筹规划，合理安排以及对各项工作的完成进度进行严密的控制，以达到用最少的时间和资源消耗来完成系统预定目标的一种计划与控制方法。

 

PERT网络是一种类似流程图的箭线图。它描绘出项目包含的各种活动的先后次序，标明每项活动的时间或相关的成本。对于PERT网络，项目管理者必须考虑要做哪些工作，确定时间之间的依赖关系，辨认出潜在的可能出问题的环节，借助PERT还可以方便地比较不同行动方案在进度和成本方面的效果。

 

构造PERT图，需要明确四个概念：事件、活动、松弛时间和关键路线。

1、事件（Events）表示主要活动结束的那一点；

2、活动（Activities）表示从一个事件到另一个事件之间的过程；

3、松弛时间（slack time）不影响完工前提下可能被推迟完成的最大时间；

4、关键路线（Critical Path）是PERT网络中花费时间最长的事件和活动的序列。

 

PERT图的作用：

1、标识出项目的关键路径，以明确项目活动的重点，便于优化对项目活动的资源分配；

2、当管理者想计划缩短项目完成时间，节省成本时，就要把考虑的重点放在关键路径上；

3、在资源分配发生矛盾时，可适当调动非关键路径上活动的资源去支持关键路径上的活动，以最有效地保证项目的完成进度；

4、采用PERT网络分析法所获结果的质量很大程度上取决于事先对活动事件的预测，若能对各项活动的先后次序和完成时间都能有较为准确的预测，则通过PERT网络的分析法可大大缩短项目完成的时间。

 

三点估计法：

所谓三点估计法就是把施工时间划分为乐观时间、最可能时间、悲观时间，也就是工作顺利情况下的时间为o，最可能时间，就是完成某道工序的最可能完成时间m，最悲观的时间就是工作进行不利所用时间p。

最可能时间（Tm）、基于最可能获得的资源、最可能取得的资源生产率、对资源可用时间的现实预计、资源对其他参与者的可能依赖以及可能发生的各种干扰等，所得到的活动持续时间。 

最乐观时间（To）、基于活动的最好情况，所得到的活动持续时间。 
最悲观时间（Tp）、基于活动的最差情况，所得到的活动持续时间。 
PERT 分析方法对以上 3 种估算进行加权平均，来计算：

活动历时均值(或估计值)=(乐观估计+4×最可能估计+悲观估计)/6

标准差SD =(悲观估计值 - 乐观估计值)/ 6

活动历时方差=(悲观估计值 - 乐观估计值)/6)²

 

标准公式如下图所示：

对于正态分布，期望值两边：

1个标准差的范围内，曲线下面积约占总面积的68.26%；

2个标准差范围内，曲线下面积约占总面积的95.44%；

3个标准差的范围内，曲线下面积约占总面积的99.72%。因此我们可以知道：

项目在期望工期完成的概率是50%，

(可能值+1个标准差)时间内完成的概率是(50%+(68.26%/2))=84.13%；

在(可能值+2个标准差)时间内完成的概率是(50%+(95.44%/2))=97.72%；

在(可能值+3个标准差)时间内完成的概率是(50%+(99.72%/2))=99.86%。

实例一、活动A乐观估计值为3天，最可能估计值为4天，悲观估计值为7天，请问A活动的均值是多少？标准差是多少？如果保证率要达到97.72%需要工期为多少天？

均值 e(t) = （7+4*4+3）/ 6 =4.33

标准差SD = （悲观值- 乐观值）/ 6 =0.67

如果要达到97.5%的可能性，加上两个方差的时间，4.33+0.67*2=5.67天

 

实例二、完成活动A悲观估计36天，最可能估计21天，乐观估计6天，请问：

（1）在16天内完成的概率是多少？

（2）在21天内完成的概率是多少？

（3）在21天之后完成的概率是多少？

（4）在21天到26天之间完成的概率是多少？

（5）在26天完成的概率是多少。

最终估算结果=（悲观工期+乐观工期+4×最可能工期）/6

标准差=（悲观-乐观）/6

带入公司计划PERT估算结果为：（36+21*4+6）/6=21

带入公式计算标准差为：（36-6）/6=5

 

所以根据正态分布：16(21-5)~26(21+5)这个区间范围内的概率都是68.26%。注：在正负一个标准差的概率有68.26%

 

算出了16~26这个区间的概率，用100%-这个区间的概率68.26%即得到了不在这个区间的概率（100%-68.26%=31.74%），

 

算出31.74%之后，再用个概率除以2即得小于16天和大于26天分别所对应的概率（31.74%/2=15.87%）

 

所以：

（1）在16天内完成的概率是多少？――15.87%（(100%-68.26)/2=15.87%）

（2）在21天内完成的概率是多少？――50%（μ=21，所以正好是50%）

（3）在21天之后完成的概率是多少？――50%（μ=21，所以正好是50%）

（4）在21天到26天之间完成的概率是多少？――68.26%/2=34.13

（5）在26天完成的概率是多少。――84.13%（100%-15.87%=84.13%或者50%+68.26%/2=84.13%）

 

实例三、A任务持续时间悲观估计为36天，最大可能估计为21天，乐观估计为6天。那么A行为在16到26天之间完成的概率有多大？

A.55.70%    B.68.26%   C.95.46% D.99.73%

解答：

（1）求出σ =（36-6）/ 6 = 5。

（2）由 σ可知21+5=26    21-5=16，因此16―26天落在1 σ分布内。

（3）由1 σ的概率P为68.26可得答案为 B、68.26%。

实例四、公司的某项目即将开始，项目经理估计该项目10天即可完成，如果出现问题耽搁了也不会超过20天完成，最快6天即可完成。根据项目历时估计中的三点估算法，你认为该项目的历时为（1）该项目历时的估算标准差为（2）。

（1）A．10天     B．11天     C．12天     D．13天

（2）A．2.1天     B．2.2天    C．2.3天    D．2.4天

解答:

（1）B    T=(6+4x10+20)/6=11

（2）C    σ=(20-6)/6=2.3

 

实例五、考虑简单的网络图，假定项目的开始时间为0,并且必须在第40天之前完成。每项活动工期的概率分布如图所示：

(1)计算期望工期

①分开计算,后加总

    活动A：（2+4*4+6）/ 6 = 4

    活动B：（5+4*13+15）/ 6 = 12

    活动C：（13+4*18+35）/ 6 = 20

把这三个分布值加总，可以得到一个总平均值，即总的te：

总te =4+12+20=36

② 先加总,再计算

总t_e= （20+4*35+56）/6 = 36

在第36天之前完成项目的概率为0.5，在第36天之后完成项目的概率也是0.5。

(2)计算活动的方差

总分布是一个正态分布，它的方差是三项活动的方差之和，即:

总方差 =0.444+2.778+13.444 = 16.666

(3)总概率分布曲线及其标准差解释

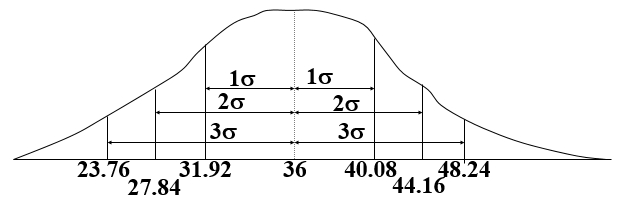
在±s范围内即

在31.92天与40.08天之间包含了总面积的68.26%；

在27.84天和44.16天之间包含了总面积的95.44%；

在23.76天与48.24天之间包含了总面积的99.72%。

 

在23.76天到48.24天之间完成项目的几率为99.72%(概率为0.997)。

在27.84天到44.16天之间完成项目的几率为95.44%(概率为0.954)。

其中：

在27.84天到36天之间完成项目的几率为47.72%（概率为0.477）

在36天到44.16天之间完成项目的几率为47.72%（概率为0.477）

在31.92天到40.08天之间完成项目的几率为68.26%(概率为0.682)

其中

在31.92天到36天的之间完成项目几率为34.13%（概率为0.341）

在36天到40.08天之间完成项目的几率为34.13%（概率为0.341）

在27.84天到31.92天之间完成项目的几率为13.5%（概率为0.135）47.72%-34.13% = 13.59%

在40.08天到44.16天之间完成项目的几率为13.5%（概率为0.135）47.72%-34.13% = 13.59%

在23.76天之前完成项目的几率为0.5%（概率为0.005）50%-49.86% = 0.14%

在48.24天之后完成项目的几率为0.5%（概率为0.005）50%-49.86% = 0.14%

 

实例五、张某是M公司的项目经理，有着丰富的项目管理经验，最近负责某电子商务系统开发的项目管理工作。该项目经过工作分解后，范围已经明确。为了更好地对项目的开发过程进行监控，保证项目顺利完成，张某拟采用网络计划技术对项目进度进行管理。经过分析，张某得到了一张工作计划表，如表1所示。

工作代号	紧前工作	计划工作历 时（天）	最短工作历 时（天）	每缩短一天所需增加的费用（万元）
A	---	5	4	5
B	A	2	2
C	A	8	7	3
D	B、C	10	9	2
E	C	5	4	1
F	D	10	8	2
G	D、E	11	8	5
H	F、G	10	9	8
每天的间接费用1万元

表1 工作计划表

 

事件1：为了表明各活动之间的逻辑关系，计算工期，张某将任务及有关属性用以下样图表示，然后根据工作计划表，绘制单代号网络图。

ES	DU	EF
ID
LS		LF

 

其中，ES表示最早开始时间；EF表示最早结束时间；LS表示最迟开始时间；LF表示最早结束时间；DU表示工作历时；ID表示工作代号。

事件2：张某的工作计划得到了公司的认可，但是项目建设方(甲方)提出，因该项目涉及融资，希望项目工期能够提前2天，并可额外支付8万元的项目款。

事件3：张某将新的项目计划上报给了公司，公司请财务部估算项目的利润。

[问题1](13分)

(1)请按照事件1的要求，帮助张某完成此项目的单代号网络图。

(2)指出项目的关键路径和工期。

[问题2](6分)

在事件2中，请简要分析张某应如何调整工作计划，才能既满足建设方的工期要求，又尽量节省费用。

[问题3](6分)

请指出事件3中，财务部估算的项目利润因工期提前变化了多少，为什么？

 

解答：

[问题1]:

依题意画出PDM单代号网络图,按下述步骤分别计算各节点的时间参数：

1.识别关键路径，关键节点浮时为0；

2.计算关键节点其他时间参数；

3.识别并行结构(看该自由节点与哪个关键节点具有相同的前置关键节点和后置关键节点)，计算自由节点浮时；

4.自由节点其他时间参数计算。

结果如下：关键路径CPM=>ACDGH，工期=44天

[问题2]:

依题意画出时间网络费用图，如下所示，其中：

1.第一行含义：节点正常工期

2.第二行含义：节点赶工后的工期

3.第三行含义：平均每天赶工的费用

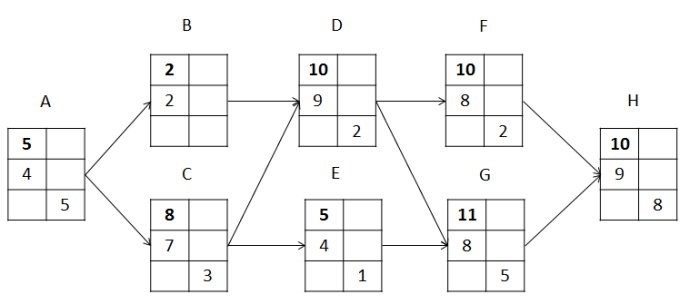
由题意可知需提供一个2天的赶工方案，同时要确保费用最低。

因为关键路径是CPM=>ACDGH,所以必须对关键路径上的关键节点进行赶工。根据成本最低原则，应该对活动C和活动D各赶工1天。

[问题3]:

由于C和D名赶工1天的成本是2+3=5万元，而每天的间接费用是1万元，所以赶工2天可以节省2万元的间接费用，而用户为赶工支付的成本是8万元，所以由于赶工而导致的利润会增加5万元(8-5+2)。

一般来讲，工程费用可分为直接费用和间接费用两大类，其中直接费用包括直接生产的工人工资及附加费，设备折旧、能源、工具及材料消耗等直接与完成活动有关的费用。为缩短活动的作业时间，需要采取一定的技术组织措施，相应地需要增加一部分直接费用，如为了赶工增加设备或者单位时间内增加能源消耗等。因此，在一定条件下和一定范围内，活动的作业时间越短，直接费用越多。间接费用通常包括管理人员的工资、办公费等,从成本会计上，我们把间接费用按照工程的施工时间进行直接分摊。在一定的生产规模内，活动的作业时间越短，分摊的间接费用也越少。

因此，我们有以下时间-费用函数：

Y = f1(t) + f2(t) 

Y：总费用 

f1(t)：直接费用 

f2(t)：间接费用