最近,跟一些朋友探讨了一下关于学习图像处理的一些问题,对于很多图像处理的问题,openCV都提供了相应的函数,那么我们还有必要自己再写一遍么?这个问题令我很头疼,估计令很多初学者都很头疼。你说不这么做吧,感觉有点点虚,毕竟用得是人家的东西,自己掌握的只是原理,或许有时候都不能拍着胸脯说自己懂这个算法了;这么做吧,当然可以更好的理解算法啦,但是,费的时间比较长,代价也是可想而知的,每天还要上课、锻炼身体,其他时间基本上都用来调Bug了,还是不够用,有时候想想这到头来能学多少呢?
讨论的结果当然不可能是说应该做哪样,应该放弃哪样,而是辩证、冷静地看待这个问题。各有各的好处,各有各的代价,首先要搞清楚自己要做什么?是专心搞工程还是做研究!要是搞工程的话,我们的一致观点就是用好openCV就好了,原理啥的可以做到纸上谈兵就好;若是要做研究,那么自己静下心来写写程序,了解各个算法,掌握各个算法的优劣和主旨思路,为自己提出新的办法是有很大帮助的!!!!!
所以你要选择哪种呢?
哎,言归正传,既然我选择这么走下去就要好好坚持,能学多少算多少!
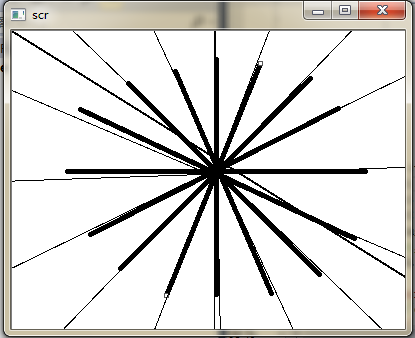
今天的主题是霍夫变换检测直线。在前面的学习中,我分别从平滑滤波、边缘检测中选择了比较经典的方法:高斯滤波、平滑滤波,为今后的学习打下了基础,那么作为我计划中最后一个入门级的任务就是简单的识别检测------霍夫变换。下文将都是自己眼中的霍夫变换,不会摘录其他文章中的话,以更好的表达自己对霍夫变换检测直线的理解。
针对检测直线,霍夫变换实际上是一种坐标变换!
大家都知道,直线在直角坐标系(x-y)中可以用一个简单的线性函数表示,如下:
Y = a * X + b
如果简单地用这个函数来寻找所有共线的(x,y),可以知道共线的(a,b)是一样的,在直角坐标系(x-y坐标系)下直观地看出是共线的,然而用编程的手法求共线是有难度的。那么我们不妨换一种形式:
b = - X * a + Y
把X,Y看作是已知数,(a,b)看作是未知数,那么所有共线的(X,Y)在参数坐标系(a-b坐标系)是共点的。共点的判断显然比共线容易很多,于是自然而然地将X-Y坐标系转换成a-b坐标系,这就是霍夫变换,从这里看是不是就是坐标变换!
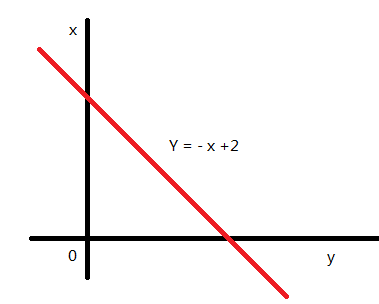 --坐标变换-->
--坐标变换--> 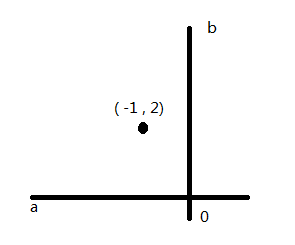
当然,看到这里,细心的读者将会提出这样一个问题:x = a的直线怎么办呢,这样直角坐标系中的斜率是不存在的!的确,如果使用直角坐标系可能这种方法还不是很完美,于是我们使用另外一种坐标系----极坐标系。标准形式如下:
Rho = X * Cos(Theta) + Y * Sin(Theta)
其中,Theta的取值范围是[ -Pi/2 , Pi/2 ],这样就可以解决直角坐标系中做不到的事情了。之后的做法与上述思路一样,将X,Y看做是已知数,Rho、Theta看做是未知数,那么共线的X,Y在参数坐标系(Rho-Theta)中就是共点的,这里不再赘述。
如上所述,每个(X,Y)点在参数坐标系中对应的是一条曲线,如果有n个点(X,Y)共线,那么这n个点在参数坐标系中对应的n条曲线中将会有一个公共点(Rho1,Theta1),于是,我们利用Theta的范围[ -Pi/2 , Pi/2 ],遍历整个图像中的边缘点,得到所有边缘像素点不同Theta所对应的Rho值,即将每个边缘点在参数坐标中相应的曲线段,找出公共点!对应程序中近似处理如下:
设置一个二维数组,Arae[Theta][Rho],初值设置为0。每当计算出一组(Rho0,Theta0),对应的二维数组元素值加1,即
Arae[Theta0][Rho0] = Arae[Theta0][Rho0] + 1
这个Arae就称作参数累加器。
在得到了所有边缘点参数坐标中的曲线后,我们查看累加器中的数值,越大就说明参数坐标系中该点共点数,转换到极坐标系也就是说更有可能是共线的,于是我们只要从大到小搜寻累加器,加以还原就可以了!
那么,又会有读者询问了,到底累加器如何通过判断数值来得到它是否是共线的呢?这里我通过查阅资料,发现有两个方法:
1.通过给定搜寻直线的条数来确定,例如,我给参数1,则只需要找到累加器中的最大值,认定其是共线参数,我给参数2,则需要找到累加器中最大值和第二大的值,认定其是共线参数...但是这样的方法是有问题的,就比如说如果是一个没有边缘的图,或者说没有直线的图,硬生生要找出n条直线出来是比较牵强的;
2.通过给定阈值,累加器大于阈值,说明可能是共线参数,否则不是,这样的话设置较为合理
我们针对图像结合编程思路来具体讨论一下这个极坐标式要注意的几点事项。
1.范围调整
如果我们要处理一张尺寸大小为M*N的图像,那么
Theta 属于 [ -Pi/2 , Pi/2 ],
Rho 属于 [ -sqrt(M^2 + N^2) , sqrt(M^2 + N^2)]
因为程序中累加器是用一个二维数组替代的,而数组标号是不允许使用负数的,于是我们需要做一些认为的调整:
Theta 属于 [ 0 , Pi ],
Rho 属于 [ 0 , 2 * sqrt(M^2 + N^2)]
2.非极大值抑制
很重要的一点是,要保证直线的准确性,进行非极大值抑制是必要的,即累加器该点值是八领域中的极大值才认可。
3.重复直线抑制
很有可能一条直线重复检测,这是不希望出现的。因此,为了防止这种现象的出现,我们要做一定的抑制:如果当前检测的直线与原来检测过的直线角度、极径都只差某个范围以内,我们可以认定是重复检测。
接下来,不可避免地要谈一谈编程的步骤了,如下:
(1)初始化一个极坐标累加器(二维数组)
(2)使用边缘检测算法(如canny算子)得到边缘检测的灰度图像
(3)扫描整个图像的前景点(边缘点),遍历整个Theta的范围得出对应的Rho值,并在对应的累加器单元加1,主要进行范围的调整
(4)寻找累加器中最大值
(5)结合所给阈值算出判断累加器共线的最小值阈值
(6)非极大值抑制
(7)得到共线的(Theta,Rho),还原到直角坐标系,并在图像显示
具体关键函数如下:
/*
这是霍夫变换的实现程序
输入参数是:img ----待处理图像
nLine----直线点的要求峰值最小值
输入之前,img需要做类似于canny之类的边缘处理
*/
IplImage* SearchLine(IplImage* img, double Through)
{
IplImage* result = cvCreateImage(cvGetSize(img), 8, 1);
double MaxDist = sqrt(img->width * img->width + img->height * img->height);//这里的rho是[-MaxDist,MaxDist]
double MaxAngle = 180;//这里的范围是0-180°
double Interval = 1;//这说明遍历的间隔是0.5度
//为霍夫坐标域分配空间:因为每算出一次对应的霍夫坐标域下的参数,则对应位置+1,故定义为int型
int AreaNum = (int)((1 / Interval )* MaxAngle * MaxDist * 2);
int **HoughArea;
vector<int> myrho;
vector<int> mytheta;
HoughArea = new int*[(int)((1/Interval)*MaxAngle)];
for (int i = 0; i < (int)((1 / Interval)*MaxAngle); ++i)
{
HoughArea[i] = new int[2 * (int)MaxDist];
}
for (int i = 0; i < (int)((1 / Interval)*MaxAngle); ++i)
{
for (int j = 0; j < 2 * (int)MaxDist; ++j)
{
HoughArea[i][j] = 0;
}
}
for (int i = 0; i < result->height; ++i)
{
for (int j = 0; j < result->width; ++j)
{
((uchar *)(result->imageData + result->widthStep * (i)))[j] = 0;
}
}
/*
step 1:开始转换到极坐标下
*/
int nDist = 0, nAngle = 0;//极坐标下计算的结果,因为要和数组结合起来,故定义成int型
double radian = 0;//弧度数
for (int i = 0; i < img->height; ++i)
{
for (int j = 0; j < img->width; ++j)
{
//cout << ((char *)(img->imageData + img->widthStep * i))[j] << endl;
//这是判断是否是前景点,只有前景点(即边缘点)才进一步处理
if (((char *)(img->imageData + img->widthStep * i))[j] == 0)
{
//开始遍历角度,计算极径,转换到极坐标下
for (nAngle = 0; nAngle < (1 / Interval)*MaxAngle; ++nAngle)
{
radian = Interval * nAngle * P / 180;
nDist = (j * cos(radian) + i * sin(radian));
nDist = nDist + MaxDist;//将rho的范围从-MaxDist,MaxDist转换到0,2*MaxDist
if (nDist < 0 || nDist > 2 * MaxDist)
{
continue;
}
HoughArea[nAngle][nDist] = HoughArea[nAngle][nDist] + 1;
}
}
}
}
/*
step 2:开始寻找nLine次最大值
*/
//定义一下清零时的角度和极径范围
int DisAllow = 10;
int AngleAllow = 5;
//定义最大值
int MaxValue = 0;
int n = 0;//找到的线条数
MaxValue = 0;
for (int i = 0; i < (int)((1 / Interval)*MaxAngle); ++i)
{
for (int j = 0; j < 2 * (int)MaxDist; ++j)
{
if (HoughArea[i][j] > MaxValue)
{
MaxValue = HoughArea[i][j];
}
}
}
cout << MaxValue << endl;
if (MaxValue == 0)
{//都等于0则不可能找得到直线
return 0;
}
int x = 0;
int throughValue = (int)((double)MaxValue * Through);
for (int i = 0; i < (int)((1 / Interval)*MaxAngle); ++i)
{
for (int j = 0; j < 2 * (int)MaxDist; ++j)
{
//cout << i << " " << j << endl;
//cout << x << endl;
//x++;
bool repeat = false;
for (int ix = 0; ix != myrho.size(); ++ix)
{
if (abs(i - mytheta[ix]) < 20 && abs(j - myrho[ix]) < 40)
{
repeat = true;
break;
}
}
if (repeat)
{
continue;
}
if (HoughArea[i][j] < throughValue)
{
continue;
}
bool isLine = true;
//非极大值抑制
for (int q = -1; q < 2; q++) {
for (int w = -1; w < 2; w++) {
if (q != 0 || w != 0) {
int yf = i + q;
int xf = j + w;
if (xf < 0) continue;
if (yf < 0) continue;
if (xf >= 2 * (int)MaxDist) continue;
if (yf >= (int)((1 / Interval)*MaxAngle)) continue;
if (HoughArea[yf][xf] <= MaxValue) {
continue;
}
}
isLine = false;
break;
}
if (isLine)
{
for (int a = 0; a < img->height; ++a)
{
for (int b = 0; b < img->width; ++b)
{
int distance = 0;//通过霍夫坐标点的theta计算rho值
distance = (int)(b * cos(Interval * i * P / 180) + a * sin(Interval * i * P / 180)) + MaxDist;
if ((distance == j))
{
((uchar *)(img->imageData + img->widthStep * (a)))[b] = 0;
}
}
}
myrho.push_back(j);
mytheta.push_back(i);
}
}
}
}
return result;
}
可以看到有几个问题:
1.重复检测问题仍然存在。这是调整重复检测参数的问题,每个图有每个图的特点,那么不一样的图应该对应不一样的参数,所以这种人工调参的方法略显笨拙,后续将探索自适应的方法;
2.检测精度不够高。这应该是非极大值抑制和阈值设置的问题
3.有严重误判。多直线共点,导致严重的共线误判,这个问题时有待解决的。
下次我将使用openCV进行霍夫变换并与此进行比对。