hdu5564--Clarke and digits（数位dp+矩阵快速幂）

Clarke and digits

问题描述

克拉克是一名人格分裂患者。某一天，克拉克变成了一个研究人员，在研究数字。  
他想知道在所有长度在$[l,r]$之间的能被$7$整除且相邻数位之和不为$k$的正整数有多少个。  

输入描述

第一行一个整数$T(1\le T\le 5)$，表示数据的组数。  
每组数据只有一行三个整数l,r,k(1≤l≤r≤109,0≤k≤18)l, r, k(1 \le l \le r \le 10^9, 0 \le k \le 18)l,r,k(1≤l≤r≤10​9​​,0≤k≤18)。  

输出描述

每组数据输出一行一个数，表示答案。由于答案太大，你只需对109+710^9+710​9​​+7取模即可。  

输入样例

2
1 2 5
2 3 5

输出样例

13
125

Hint

第一个样例有13个数满足，分别是：$7,21,28,35,42,49,56,63,70,77,84,91,98$

 

花了挺久想明白，决定细写一下。

考虑dp，令d(i,j,k)表示长度为i第i位为j余数为k的方案数
则d(1,j,j%7) = 1, 0<j<10 d(i+1,x,(k*10+x)%7)+=d(i,j,k)
发现转移相同，所以我们用矩阵快速幂来计算即可。
dp[k][j] 首位为j 余数为k的方案数
把dp写成一维 dp[k*10+j]

 

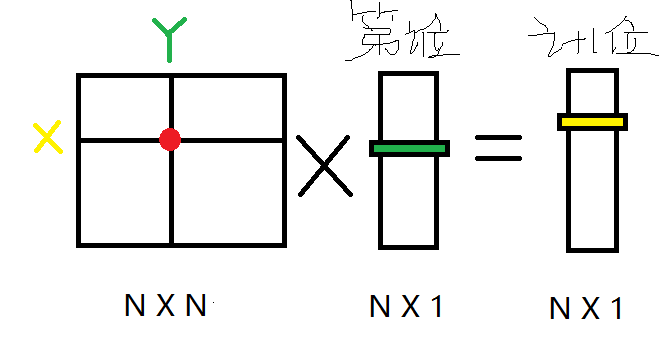
用一个一维矩阵来每一位数表示所有的状态，相邻位之间的转移相同，构造一个矩阵来表示转移方程。然后矩阵快速幂解决问题。

由于线代没学好，遇到矩阵的问题头疼的很……于是我画图理解了一下。

啊啊，反正大概就是这样……

然后加一长度是为了记录答案。

 

 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const ll MOD = 1000000007;

typedef vector<ll> vec;
typedef vector<vec> mat;

mat mul(mat &A, mat &B)
{
	mat C(A.size(), vec(B[0].size()));
	for (int i = 0; i < A.size(); ++i) {
		for (int k = 0; k < B.size(); ++k) {
			for (int j = 0; j < B[0].size(); ++j) {
				C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % MOD;
			}
		}
	}
	return C;
}

mat pow(mat A, int n)
{
	mat B(A.size(), vec(A.size()));
	for (int i = 0; i < A.size(); ++i)
		B[i][i] = 1;
	while (n > 0) {
		if (n & 1) B = mul(B, A);
		A = mul(A, A);
		n >>= 1;
	}
	return B;
}

ll cal(int num, int n)
{
    mat f(71, vec(71));
    for (int i = 0; i < 7; ++i) {
        for (int j = 0; j <= 9; ++j) {
            for (int k = 0; k <= 9; ++k) {
                if (j + k == num) continue;
                int x = (i * 10 + k) % 7;
                f[x * 10 + k][i * 10 + j]++;
            }
        }
    }
    f[70][70] = 1;
    for (int i = 0; i <= 9; ++i)
        f[70][0 * 10 + i] = 1;

    mat v(71, vec(1));
    for (int i = 1; i <= 9; ++i) {
        v[(i % 7) * 10 + i][0] = 1;
    }
    f = pow(f, n);
    v = mul(f, v);
    return v[70][0];
}


int main()
{
    int t;
    scanf("%d", &t);
    while (t--) {
        //l,r,k(1≤l≤r≤109,0≤k≤18)
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);
        ll ans = (cal(k, r) - cal(k, l - 1) + MOD) % MOD;
        printf("%lld\n", ans);
    }
    return 0;
}