基础算法(一)

首先必须得说本人对算法研究不深，一些简单的就得想半天，老是这样感觉不太好，遂记录下一些常见的基础算法，避免尴尬。不足之处请各位多多指教。

其次，用vs写C语言程序时可能会出现如下错误：
错误 C4996 'scanf': This function or variable may be unsafe. Consider using scanf_s instead. To disable deprecation, use _CRT_SECURE_NO_WARNINGS. See online help for details.

解决方法1：在代码的开头加上这句  #pragma warning(disable:4996)

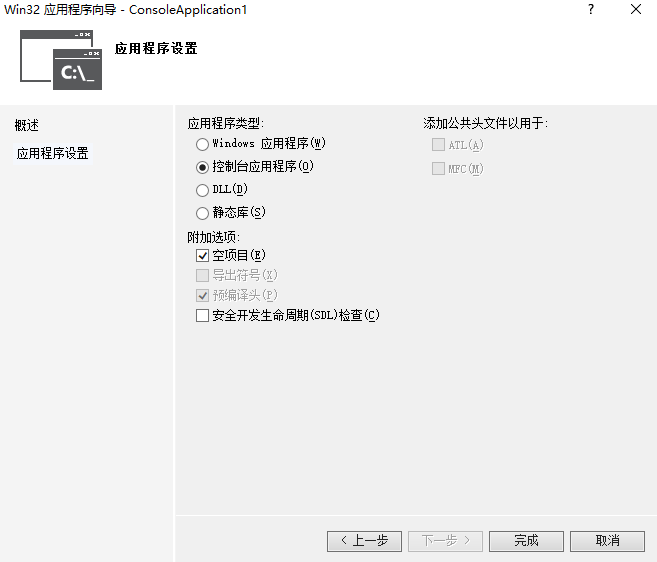
解决方法2：在创建项目时按下图进行选中：

最后，进入正题。。。

1.最大公约数

    01.短除法：我们小学学习的用来求最大公约数的方法，体现在代码中主要的操作就是比较和累乘。

#include<stdio.h>
int main()
{
    int a, b, t, i;
    scanf("%d%d", &a, &b);
    t = 1;
    for (i = 2; i <=a&&i<=b; i++)
    {
        while (a%i==0&&b%i==0)
        {
            t = t*i;
            a = a / i;
            b = b / i;
        }
    }
    printf("Maximal common divisor is %d\n", t);
    return 0;
}

   02.辗转相除法：它根据递推策略设计的，求解效率更高。   

#include<stdio.h>
int main()
{
    int a, b,c;
    scanf("%d%d", &a, &b);//输入的时候注意：a>b
    if (b==0)
    {
        printf("data error.\n");
        return 0;
    }
    else
    {
        c = a%b;
        while (c!=0)
        {
            a = b;
            b = c;
            c = a%b;
        }
    }
    
    printf("Maximal common divisor is %d\n", b);
    return 0;
}

    03相减法：两数中的大数减小数，其差与减数再进行大数减小数，直到差与减数相等为止，此时的差或者减数就是最大公约数。

#include<stdio.h>
int main()
{
    int a, b, c;
    scanf("%d%d", &a, &b);//输入的时候注意：a>b
    c = a - b;
    while (c!=b)
    {
        if (b > c)
        {
            a = b;
            b = c;
        }
        else
        {
            a=c;
        }
        c = a - b;
    }
    printf("Maximal common divisor is %d\n", b);
    return 0;
}

 

2.最小公倍数

  在我们已经求出最大公约数的情况下，再求最小公倍数就很容易了。下面给出的是短除法求得最大公约数之后求最小公倍数的方法：

#include<stdio.h>
int main()
{
    int a, b, t, i;
    scanf("%d%d", &a, &b);
    t = 1;
    for (i = 2; i <= a&&i <= b; i++)
    {
        while (a%i == 0 && b%i == 0)
        {
            t = t*i;
            a = a / i;
            b = b / i;
        }
    }
    printf("Minimal common multiple is %d\n", t*a*b);
    return 0;
}

 

3.素数

 这个好像有点尴尬，算法课上，老师点了两个同学到黑板上去写，然后两个都写得不太对。。。后来想想，作为大三，真的。。。可能是一时被点还有点没反应过来吧。

#include<stdio.h>
#include<math.h>
int main()
{
    int k, n,i,x;
    while (scanf("%d", &x) != 0)
    {
        n = sqrt(x);
        i = 0;
        for (k = 2; k <= n; k++)
            if (x%k == 0)
            {
                i = 1;
                printf("%d is not a prime number.\n",x);
                break;
            }
        if (i == 0)
            printf("%d is  a prime number.\n", x);
    }
    return 0;
}

4.完数

   一个数如果恰好等于它的因子之和，这个数就称为”完数“，6的因子为1，2，3，而6=1+2+3,所以6就是完数。

#include<stdio.h>
int main()
{
    int i, m, s;
    for (m = 2; m < 1000; m++)
    {
        s = 0;
        for (i = 1; i < m; i++)
            if (m%i == 0)
                s += i;
        if (s == m)
        {
            printf("%d,its factors are ", m);
            for (i = 1; i < m; i++)
                if (m%i == 0)
                    printf("%d ", i);
            printf("\n");
        }
    }
    return 0;
}

5.裴波那挈数列  

   裴波那挈数列具有以下特点：

        a1,a2已知

        a(n)=a(n-1)+a(n-2)  n>=3

   我们在很多地方都会遇到这个数列，比如兔子繁殖问题、树枝问题、上楼方式问题、蜂房问题等等。我们既可以用递推，也可以用递归的方法来解决。

//递推
#include<stdio.h>
int main()
{
    int a = 1, b = 1;
    printf("%d %d ", a,b);
    while (a<5000)
    {
        a = a + b;
        b = a + b;
        printf("%d %d ", a, b);
    }

    return 0;
}

 

//递归
#include<stdio.h>
int f(int n)
{
    if (n == 1 || n == 2)
        return 1;
    else
        return f(n - 1) + f(n - 2);
}
int main()
{
    int i;
    for (i = 1; i < 20; i++)
        printf("%d ", f(i));
    printf("\n");
    return 0;
}

6.杨辉三角

 1

 1   1

 1   2   1

 1   3   3   1

 1   4   6   4   1

 ............................

 杨辉三角是（a+b)^n （n>=0）展开后各项的系数，具有以下规律：

 1.各行的第一个数和最后一个数都是1

 2.从第3行起，除第一个数和最后一个数外，其余各数是上一行同列和前一列两个数之和。即a[i][j]=a[i-1][j]+a[i-1][j-1]  （i表示行数，j表示列数）

#include<stdio.h>
const int N = 10;
int main()
{
    int i, j;
    int a[N][N];
    for (i = 0; i < N; i++)
    {
        for (j = 0; j <=i; j++)
            if (j == 0 || j ==i)
                a[i][j] = 1;
            else 
                a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
    }

    for (i = 0; i < N; i++)
    {
        for (j = 0; j <=i; j++)
            printf("%6d", a[i][j]);
        printf("\n");
    }

    return 0;
}

7.魔方阵

   魔方阵，它的每一行，每一列以及对角线上的各数之和为一个相同的常数。

   这里只考虑了奇次阶魔方阵，数组下标是从1~n。

#include<stdio.h>
int main()
{
    int i, j, i1, j1, x, n, a[100][100];
    printf("input an odd number:");
    scanf("%d", &n);
    if (n % 2 == 0)
    {
        printf("input error!\n");
        return 0;
    }
    for (i = 1; i <= n; i++)
        for (j = 1; j <= n; j++)
            a[i][j] = 0;

    i = 1;
    j = (int)(n+1)/ 2;
    x = 1;
    while (x <= n*n)
    {
        a[i][j] = x;
        x = x + 1;
        i1 = i;
        j1 = j;
        i = i -1;
        j = j - 1;
        if (i == 0) i = n;
        if (j == 0) j = n;
        if (a[i][j] != 0)
        {
            i = i1 + 1;
            j = j1;
        }
    }
        for (i = 1; i <= n; i++)
        {
            for (j = 1; j <= n; j++)
                printf("%5d", a[i][j]);
            printf("\n");
        }
}

 

8.汉诺塔问题

   简单的说就是有A，B，C三个基座，要将A座上的盘子移动到B座，在移动的过程中3个基座上的盘子都必须保持大盘在下，小盘在上，可以利用C座做辅助。

   记得大一的时候，怎么都不太懂，那个时候好像题目都没太读懂，然后不理解递归，就一直害怕这个。

   我们把n个盘子抽象地看作是“两个盘子”，上面一个由1~n-1号组成，下面一个就是第n号盘子，移动过程如下：

   1.先把上面一个盘子以A基座为起点借助B基座移动到C基座，

   2.把下面一个盘子从A基座移动到B基座，

   3.再把C基座上的一个盘子借助A基座移动到B基座。

#include<stdio.h>
void hanoi(int n, char a,char b,char c);
int main()
{
    int n;
    scanf("%d", &n);
    hanoi(n, 'A', 'B', 'C');
}

void hanoi(int n, char a, char b, char c)
{
    if (n > 0)
    {
        hanoi(n - 1, a, c, b);
        printf("Move dish %d from pile %c to %c.\n", n, a, b);
        hanoi(n - 1, c, b, a);
    }
}

9.整数的划分问题

   对于一个正整数的划分，就是把n表示成一系列正整数之和的表达式。例如n=6的划分如下：

   6

   5+1   

   4+2   4+1+1

   3+3   3+2+1   3+1+1+1

   2+2+2    2+2+1+1    2+1+1+1+1

   1+1+1+1+1+1

   问题：对于给定的正整数n，求出它划分的数目

   根据n=6的实例发现：第一行及以后的数据都不超过6，第二行及以后的数据都不超过5，......第六行的数据都不超过1.据此，定义一个函数Q(n,m),表示整数n的“任何加数都不超过m"的分划得数目，n的所有划分的数目就是Q(n,n)

   一般Q(n,m)有以下递归关系：

   Q(n,n)=1+Q(n,n-1)        

   Q(n,n)=Q(n,m-1)+Q(n-m,m)   (n>m)

  递归的停止条件：

  Q(n,1)=1

  Q(1,m)=1

#include<stdio.h>

int Divinteger(int n, int m);
int main()
{
    int n;
    scanf("%d", &n);
    if (n < 1)
    {
        printf("Input error!\n");
        return 0;
    }

    printf("%d\n", Divinteger(n, n));
}

int Divinteger(int n, int m)
{
    if (n == 1 || m == 1)
        return 1;
    else if (n < m)
        return Divinteger(n, n);
    else if (n == m)
        return 1 + Divinteger(n, n - 1);
    else
        return Divinteger(n, m - 1) + Divinteger(n - m, m);
}

 

10.开灯问题

   有从1到n依次编号的n个同学和n盏灯。1号同学将所有的灯都关掉，2号同学将编号为2的倍数的灯都打开，3号同学将编号为3的倍数的灯都关掉，.......以后的同学都将自己编号的倍数的灯做相反的处理。（该号灯如是打开的，则关掉；如关闭的，则打开）。问经n个同学操作后，哪些灯是打开的

   1.定义n个元素的a数组，它的每个下标变量a[i]视为一灯，i表示其编号。a[i]=1表示第i盏灯处于打开状态，a[i]=0表示第i盏灯处于关闭状态。

   2.通过算术运算a[i]=1-a[i]（乒乓开关）,模拟“开关”灯的操作。

#include<stdio.h>
int main()
{
    int n, a[1000], i, k;
    printf("input a number:");
    scanf("%d", &n);
    for (i = 1; i <=n; i++)
    {
        a[i] = 0;
    }
    for (i = 2; i <=n; i++)
    {
        k = 1;
        while (i*k<=n)
        {
            a[i*k] = 1 - a[i*k];
            k++;
        }
        for (i = 1; i <=n; i++)
        {
            if (a[i] == 1)
                printf("%d ",i);
        }
        printf("\n");
    }
}

好了，就到这里，下次见！