【线性代数】 03 - 行列式
1. 行列式的定义
线性方程组中比较常见的是\(m=n\)的情况,我们想知道这种方程组什么时候有唯一解?并且如何用系数表示这个唯一解?对于元数较少的方程,可以直接用消元法得到解的具体公式,比如(1)式就是二元方程组的公式解。公式中重复出现了模式\(ab-cd\),这个模式不仅能判断方程组是否有唯一解,还能直接表示解的公式。
\[x_1=\dfrac{b_1a_{22}-b_2a_{21}}{a_{11}a_{22}-a_{12}a_{21}};\quad x_2=\dfrac{a_{11}b_2-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}}\tag{1}\]
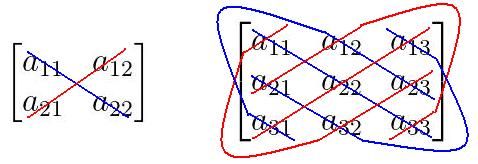
考虑到二元方程组的系数矩阵(下式左),上面的模式表现为对角线积的差。同样对三元方程组,我们也可以得到重复的模式,分母为\(a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}\),参照系数矩阵(下式右)可知,模式表现为正反斜线的差。
我们现在自然想问,对任意\(m=n\)的线性方程组,是否都有这样的模式?它的一般表达式是什么?经过考察更多元的方程组,数学家们还真找到了一般的表达式,式子由所有\(a_{1j_1}a_{2j_2}\cdots a_{nj_n}\)形式的乘积组成,其中\((j_1j_2\cdots j_n)\)是\(1\sim n\)的一个排列。另外,每一项的符号由排列\((j_1j_2\cdots j_n)\)的逆序数\(\tau(j_1j_2\cdots j_n)\)决定,如果逆序数为偶数则为正,否则为负。设系数矩阵为\(A\),则这个表达式被称为\(A\)的行列式(determinant),记作\(|A|\),总结有它的值为公式(2)。
\[|A|=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}=\sum_{j_1j_2\cdots j_n}{(-1)^{\tau(j_1j_2\cdots j_n)}a_{1j_1}a_{2j_2}\cdots a_{nj_n}}\tag{2}\]
逆序数的概念之前介绍过,这里再简单阐述一下。排列\((j_1j_2\cdots j_n)\)中,如果有\(p<q\)但\(j_p>j_q\),则\(j_pj_q\)称为一个逆序,所有逆序的个数叫排列的逆序数,记作\(\tau(j_1j_2\cdots j_n)\)。在实际应用场合,其实更有用的是逆序数的奇偶性,对应就有奇排列和偶排列的概念。容易证明,任意两数的对换会改变排列的奇偶性,而两个排列之间都可以通过一系列对换进行转换,故奇偶性也可以通过对换次数来判断。
行列式的项数正是全排列的个数\(n!\),并且显然其中奇偶排列各占一半。行列式的每一项是在每一行取列号不同的元素,其实它等价于取\(n\)个行列号都不同的元素\(a_{x_1y_1}a_{x_2y_2}\cdots a_{x_ny_n}\),特别地它还等价于在每一列中取行号不同的元素\(a_{i_11}a_{i_22}\cdots a_{i_nn}\)。由于\(a_{x_py_p},a_{x_qy_q}\)对调后\((x_1x_2\cdots x_n)\)和\((y_1y_2\cdots y_n)\)的奇偶性同时变化,故它们的和是不变的,这样就得到公式(3)的关系。
\[(-1)^{\tau(x_1x_2\cdots x_n)+\tau(y_1y_2\cdots y_n)}=(-1)^{\tau(i_1i_2\cdots i_n)}=(-1)^{\tau(j_1j_2\cdots j_n)}\tag{3}\]
行列式最初被发现时,只是为了表达线性方程组的解,但在后面的线性变换和空间的度量中,它却成了不可或缺的工具。行列式定义的计算量比较大,我们往往只能用它来计算一些简单矩阵的行列式,比如可以直接计算如下上(下)三角形行列式。
\[\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\0&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&a_{nn}\end{vmatrix}=\begin{vmatrix}a_{11}&0&\cdots&0\\a_{21}&a_{22}&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}=a_{11}a_{22}\cdots a_{nn}\tag{4}\]
• 求行列式:\(\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1(n-1)}&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2(n-1)}&0\\\vdots&\vdots&\ddots&\vdots&\vdots\\a_{n1}&0&\cdots&0&0\end{vmatrix}\),\(\begin{vmatrix}0&a_1&0&\cdots&0\\0&0&a_2&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&a_{n-1}\\a_n&0&0&\cdots&0\end{vmatrix}\),\(\begin{vmatrix}a_1&a_2&a_3&a_4&a_5\\b_1&b_2&b_3&b_4&b_5\\0&0&0&c_1&c_2\\0&0&0&d_1&d_2\\0&0&0&e_1&e_2\end{vmatrix}\)。
2.行列式的初等变换
既然三角形行列式比较容易计算,我们希望通过初等变换将行列式三角化,为此需要了解初等变换对行列式的影响。首先根据定义容易知道,对行列式的某一行(列)乘上常数\(k\),行列式的值也变成\(k\)倍(公式(5))。从而如果有某行(列)全为\(0\),行列式的值也为\(0\)。另外,将行列式的两行(列)交换,将翻转每一项的奇偶性,故行列式的值取相反数(公式(6))。从而如果某两行(列)相等,行列式值为\(0\),再结合公式(5)知,某两行(列)成比例的行列式值也为\(0\)。
\[\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\\vdots&\vdots&\ddots&\vdots\\ka_{i1}&ka_{i2}&\cdots&ka_{in}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}=k\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\\vdots&\vdots&\ddots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}\tag{5}\]
\[\begin{vmatrix}\vdots&\vdots&\ddots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\ddots&\vdots\\a_{j1}&a_{j2}&\cdots&a_{jn}\\\vdots&\vdots&\ddots&\vdots\end{vmatrix}=-\begin{vmatrix}\vdots&\vdots&\ddots&\vdots\\a_{j1}&a_{j2}&\cdots&a_{jn}\\\vdots&\vdots&\ddots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\ddots&\vdots\end{vmatrix}\tag{6}\]
第三个初等变换是将行(列)的倍数加到另一行(列),而首先由定义知,在在一行(列)同时加上一些数,等于两个行列式的和(公式(7))。从而第三个初等变换得到两个行列式(公式(8)),第一个是它本身,第二个的第\(j\)行是第\(i\)行倍数,故为\(0\)。
\[\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\\vdots&\vdots&\ddots&\vdots\\b_1+c_1&b_2+c_2&\cdots&b_n+c_n\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\\vdots&\vdots&\ddots&\vdots\\b_1&b_2&\cdots&b_n\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}+\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\\vdots&\vdots&\ddots&\vdots\\c_1&c_2&\cdots&c_n\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}\tag{7}\]
\[\begin{vmatrix}\vdots&\vdots&\ddots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\ddots&\vdots\\a_{j1}+ka_{i1}&a_{j2}+ka_{i2}&\cdots&a_{jn}+ka_{in}\\\vdots&\vdots&\ddots&\vdots\end{vmatrix}=\begin{vmatrix}\vdots&\vdots&\ddots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\ddots&\vdots\\a_{j1}&a_{j2}&\cdots&a_{jn}\\\vdots&\vdots&\ddots&\vdots\end{vmatrix}\tag{8}\]
由上面的讨论可知,初等变换(不包括乘以\(0\))只会使行列式的值乘以一个非零值,如果我们只关心行列式是否为\(0\),初等变换并不影响结果。具体到\(m=n\)的线性方程组中,用初等变换将系数矩阵变为上三角形,方程有唯一解的充要条件是对角线都是非零值,这就等价于原系数矩阵的行列式非零。对\(n\)维线性空间,任意\(n\)个向量线性无关的充要条件是:坐标矩阵的行列式非零,两组基之间的过渡矩阵的行列式显然非零。
灵活使用初等变换,可以简化行列式的求解,有些问题还需要较强技巧,考虑以下问题。
• 计算行列式:\(\begin{vmatrix}\lambda&a&a&\cdots&a\\a&\lambda&a&\cdots&a\\\vdots&\vdots&\vdots&\ddots&\vdots\\a&a&a&\cdots&\lambda\end{vmatrix}\),\(\begin{vmatrix}x_1-a_1&x_2&x_3&\cdots&x_n\\x_1&x_2-a_2&x_3&\cdots&x_n\\\vdots&\vdots&\vdots&\ddots&\vdots\\x_1&x_2&x_3&\cdots&x_n-a_n\end{vmatrix}\),\(\begin{vmatrix}a_1&a_2&a_3&\cdots&a_n\\b_2&1&0&\cdots&0\\b_3&0&1&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\b_n&0&0&\cdots&1\end{vmatrix}\);
• 记\(A\)的每个元素加上\(t\)后的矩阵为\(A(t)\),求证:\(|A(t)|=|A|+t\sum\limits_{i=1}^n\sum\limits_{j=1}^n{A_{ij}}\)。
3. 行列式的分解
3.1 按一行(列)展开
如果要继续研究行列式,一个容易想到的方向就是行列式的分解。对行列式的\(n!\)项,也许我们可以对它们进行分类和聚拢,从而得到有意义的分割。根据行列式的定义,每一项其实是在每一行(列)中各取一个元素,一个比较自然的分割方法就是:按第\(i\)行(\(j\)列)的元素分成\(n\)类,而含有\(a_{ik}\)(\(a_{kj}\))的项属于一类。设同一类项的和为\(a_{ik}A_{ik}\)(\(a_{kj}A_{kj}\)),则有下式成立,其中其中\(A_{ij}\)称也为\(a_{ij}\)的代数余子式。
\[|A|=\sum_{k=1}^n{a_{ik}A_{ik}}=\sum_{k=1}^n{a_{kj}A_{kj}}\tag{9}\]
为了方便讨论,把\(|A|\)去除第\(i\)行、第\(j\)列后的行列式叫做\(a_{ij}\)的余子式(cofactor),并记为\(M_{ij}\)。仔细考察\(A_{ij}\)的每一项,根据行列式的定义,它们正好与\(M_{ij}\)的每一项一一对应。只不过在\(A_{ij}\)中是\(a_{1j_1}\cdots a_{ij}\cdots a_{nj_n}\)的奇偶性,而在\(M_{ij}\)中是\(a_{1j_1}\cdots a_{(i-1)j_{i-1}}a_{(i+1)j_{i+1}}\cdots a_{nj_n}\)的奇偶性。容易证明两者逆序数相差\(i+j\),从而有\(A_{ij}=(-1)^{i+j}M_{ij}\),公式(9)可以改写为公式(10)。
\[|A|=\sum_{k=1}^n{(-1)^{i+k}a_{ik}M_{ik}}=\sum_{k=1}^n{(-1)^{k+j}a_{kj}M_{kj}}\tag{10}\]
公式(10)以一行(列)展开行列式,它给出了计算行列式的一个降阶方法,在某些形式的行列式中非常有用。比如当行列式的某行(列)的非零数很少时(或者在一些初等变换之后),那么以这一行(列)展开计算就很快速。尝试计算以下行列式:
• 计算行列式:\(\begin{vmatrix}a&b&0&\cdots&0\\0&a&b&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&b\\b&0&0&\cdots&a\end{vmatrix}\),\(\begin{vmatrix}1&2&3&\cdots&n\\n&1&2&\cdots&n-1\\\vdots&\vdots&\vdots&\ddots&\vdots\\2&3&4&\cdots&1\end{vmatrix}\);
• 求证:\(\begin{vmatrix}x&0&\cdots&0&a_0\\-1&x&\cdots&0&a_1\\0&-1&\cdots&0&a_2\\\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&\cdots&-1&x+a_{n-1}\end{vmatrix}=x^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\)。
以下左式是著名的范德蒙行列式(Vandermonde),在每一行上减掉上一行的\(a_1\)倍,第\(1\)列只有\(a_{11}\)非零,故行列式等于\(M_{11}\)。\(M_{11}\)每一列提取出公倍数\(a_j-a_1\)就得到\(a_2,\cdots,a_n\)上的范德蒙行列式,以此类推就得到\(n\)阶范德蒙行列式的值(公式(11))。由公式(11)可知,范德蒙行列式等于\(0\)的充要条件是存在\(a_i=a_j\)。这个行列式形式独特,在数学的各个分支都有应用,经常出现于一些构造无关向量的场合中。
\[\begin{vmatrix}1&1&\cdots&1\\a_1&a_2&\cdots&a_n\\a_1^2&a_2^2&\cdots&a_n^2\\\vdots&\vdots&\ddots&\vdots\\a_1^{n-1}&a_2^{n-1}&\cdots&a_n^{n-1}\end{vmatrix}=\begin{vmatrix}1&1&\cdots&1\\0&(a_2-a_1)&\cdots&(a_n-a_1)\\0&a_2(a_2-a_1)&\cdots&a_n(a_n-a_1)\\\vdots&\vdots&\ddots&\vdots\\0&a_2^{n-2}(a_2-a_1)&\cdots&a_n^{n-2}(a_n-a_1)\end{vmatrix}\\ =\sum_{j=1}^n(a_j-a_1)\cdot\begin{vmatrix}1&\cdots&1\\a_2&\cdots&a_n\\\vdots&\ddots&\vdots\\a_2^{n-2}&\cdots&a_n^{n-2}\end{vmatrix}=\sum_{1\leqslant i<j\leqslant n}(a_j-a_i)\tag{11}\]
有时候像范德蒙行列式一样,按行(列)展开并不能直接得到结果,而是一个递推式,解递推式方程即可得到行列式的值。这样的行列式往往具有很规律的结构,在实际应用中经常会碰到,一些常见的行列式最好直接记住它的结论。
• 计算行列式:\(\begin{vmatrix}2&-1&0&\cdots&0&0\\-1&2&-1&\cdots&0&0\\0&-1&2&\cdots&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&\cdots&2&-1\\0&0&0&\cdots&-1&2\end{vmatrix}\)。
3.2 拉普拉斯定理
上面按一行(列)展开了行列式,其实这个结论可以很容易扩展到按\(k\)行(列)展开。之前我们以一行(列)的每个元素为分类依据,现在则是要以\(k\)行(列)中每个\(k\)阶子行列式为分类依据。记第\(i_1,i_2,\cdots,i_k\)行、第\(j_1,j_2,\cdots,j_k\)列的元素组成的行列式为\(A\begin{pmatrix}i_1\cdots i_k\\j_1\cdots j_k\end{pmatrix}\),剩下的\(n-k\)行、\(n-k\)列组成的行列式称为它的余子式,比如是\(A\begin{pmatrix}i'_1\cdots i'_{n-k}\\j'_1\cdots j'_{n-k}\end{pmatrix}\)。
如果要按第\(i_1,i_2,\cdots,i_k\)行展开,则将行列式所有项按照\(A\begin{pmatrix}i_1\cdots i_k\\j_1\cdots j_k\end{pmatrix}\)分类,其中\(j_1\cdots j_k\)取\(1\sim n\)中所有\(k\)个数的组合。类似上面的证明思路,可知每一类的符号是\((-1)^{i_1+\cdots+i_k+j_1+\cdots+j_k}\),所以有如下按\(k\)行展开行列式的拉普拉斯定理(Laplace),按列展开类似。
\[|A|=\sum_{1\leqslant j_1<\cdots<j_k\leqslant n}{(-1)^{i_1+\cdots+i_k+j_1+\cdots+j_k}A\begin{pmatrix}i_1\cdots i_k\\j_1\cdots j_k\end{pmatrix}A\begin{pmatrix}i'_1\cdots i'_{n-k}\\j'_1\cdots j'_{n-k}\end{pmatrix}}\tag{11}\]
拉普拉斯定理多用于有块状特征的行列式,设\(A,B,C,D\)分别是\(s\times s,t\times t,t\times s,s\times t\)的矩阵块,则容易有公式(12)的结论。
\[\begin{vmatrix}A&0\\C&B\end{vmatrix}=\begin{vmatrix}A&D\\0&B\end{vmatrix}=|A||B|\tag{12}\]
• 计算行列式:\(\begin{bmatrix}A&B\\B&A\end{bmatrix}\),其中\(A=\begin{bmatrix}a&&\\&\ddots&\\&&a\end{bmatrix},\:B=\begin{bmatrix}&&b\\&{\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu\raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}}&\\b&&\end{bmatrix}\)。
4. 行列式技巧举例
行列式根据定义总是可以计算出来的,但实际问题中的很多行列式具有特殊的格式,而且需要得到一般的表达式。除了上面的基本工具,有时需要很多的技巧,这要求有较高的数学综合素养。我们虽然不建议搞题海战术,但不得不承认技巧和思想在数学中都是不可缺少的,而这需要一些锻炼和总结。我们经常会碰到一些具有特定规律的行列式,需要根据这些规律找到适合它的方法和技巧。
有一种行列式,它的每行(列)非常相似,但又总有一点不同,这时需要想办法提取出相同的部分。一种做法是将相同的部分单独作为新的一行(列)加到矩阵中,然后进行消除,便会得到较简单的形式,我们可以把它叫做加边法。比如以下左式,可以给它添加一行\([1\:a_1\:a_2\:\cdots\:a_n]\)(第一列其它元素为零)。还有一种做法就是将每一行(列)中不同的部分剥离开来,分别计算两个简单的行列式。比如以下右式,可以将第一个\(x\)拆成\(y+(x-y)\),接下来的递归式就容易了。
\[\begin{vmatrix}b_1&a_2&a_3&\cdots&a_n\\a_1&b_2&a_3&\cdots&a_n\\a_1&a_2&b_3&\cdots&a_n\\\vdots&\vdots&\vdots&\ddots&\vdots\\a_1&a_2&a_3&\cdots&b_n\end{vmatrix},\quad\begin{vmatrix}x&y&\cdots&y&y\\z&x&\cdots&y&y\\\vdots&\vdots&\ddots&\vdots&\vdots\\z&z&\cdots&x&y\\z&z&\cdots&z&x\end{vmatrix}\]
当行列式表现为一个多项式时,我们可以把注意力集中到确定多项式的系数上,这个方法叫待定系数法。比如以下左式,多项式的\(n+1\)个根是可以猜出来的,多项式也就可以得到。再比如以下右式,它可以看做是\(n+1\)阶范德蒙行列式的一个余子式。以\(x\)补完最后一列,范德蒙行列式为多项式,且刚才的余子式便是\(x^{n-1}\)项的系数(注意符号)。
\[\begin{vmatrix}x&a_1&a_2&\cdots&a_n\\a_1&x&a_2&\cdots&a_n\\a_1&a_2&x&\cdots&a_n\\\vdots&\vdots&\vdots&\ddots&\vdots\\a_1&a_2&a_3&\cdots&x\end{vmatrix},\quad\begin{vmatrix}1&1&\cdots&1\\a_1&a_2&\cdots&a_n\\a_1^2&a_2^2&\cdots&a_n^2\\\vdots&\vdots&\ddots&\vdots\\a_1^n&a_2^n&\cdots&a_n^n\end{vmatrix}\Rightarrow\begin{vmatrix}1&1&\cdots&1&1\\a_1&a_2&\cdots&a_n&x\\\vdots&\vdots&\ddots&\vdots\\a_1^{n-1}&a_2^{n-1}&\cdots&a_n^{n-1}&x^{n-1}\\a_1^n&a_2^n&\cdots&a_n^n&x^n\end{vmatrix}\]
还有一种方法难度比较大,需要借助公式\(|AB|=|A||B|\)(见下篇)。有一些行列式可以先分解成两个简单行列式的积,比如以下左式(\(s_k=x_1^k+x_2^k+\cdots+x_n^k\))是两个范德蒙行列式的积。还有一些行列式可以形成较好的乘法等式,而该等式有助于计算行列式,比如以下右式的循环矩阵,考虑到\(n\)次本原单位根\(\omega\)幂次的循环性,你可以尝试将它乘上由\(1,\omega,\omega^2,\cdots,\omega^{n-1}\)组成的范德蒙行列式。
\[\begin{vmatrix}s_0&s_1&\cdots&s_n\\s_1&s_2&\cdots&s_{n+1}\\\vdots&\vdots&\ddots&\vdots\\s_n&s_{n+1}&\cdots&s_{2n}\end{vmatrix},\quad\begin{vmatrix}a_1&a_2&\cdots&a_n\\a_n&a_1&\cdots&a_{n-1}\\\vdots&\vdots&\ddots&\vdots\\a_2&a_3&\cdots&a_1\end{vmatrix}\]