算法导论 第十二章 二叉搜索树（python）

上图：

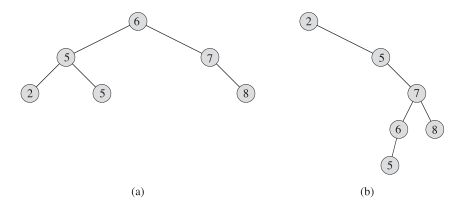
这是二叉搜索树（也有说是查找树的）基本结构：如果y是x的左子树中的一个结点，那么y.key <= x.key(如a图中的6根结点大于它左子树的每一个结点 6 >= {2,5,5}),如果y是x的右子树中的一个结点，那么y.key >x.key

注：不同堆，堆是中间的结点最大或最小，而二叉搜索树是左中右的大小顺序，我们用这个特性来遍历二叉搜索树得到是他的顺序排列（中序遍历）#中在什么地方就叫什么遍历 如前序遍历：中左右  后序：左右中

如图a他的中序遍历为 2->5->5->6->7->8 #从大到小

基本操作：

SEARCH：查找关键字为k的结点  O(h) #h为二叉树的高度

MINIMUM:查找二叉树的最小值（显然是最左的那个结点） O(h)

MAXIMUM:查找二叉树的最大值（显然是最右的那个结点） O(h)

PREDECESSOR:查找x的前驱y O(h)

SUCCESSOR:查找x的后驱y O(h)

INSERT:插入结点z O(h)

DELETE:删除结点z O(h)

注：

1.其中插入和删除因为要调整树的结构所以有点复杂

2.复杂都为O(h) #h为二叉树的高度,我们看下图

他们的结点数（n）都是6但是高度是不同的 ha = 2 而 hb = 4 ，这种差距在应用中可能会有很大的性能问题，同以前的快速排序一样使用随机化方法或者是其他的限定条件（如红黑树）来保证性能在一个好一点的范围内（h = logn），就是不能让二叉树保持一条直线向下

给出python实现：

class Node: #结点

    def __init__(self,data):
        self.left = None
        self.right = None
        self.parent = None
        self.data = data
    def createNode(self,data):
        #初始化
        return Node(data)
    
    def inorder_tree_walk(self):
        """
        中序遍历
        """
        if self.left: #左
            self.left.inorder_tree_walk()
        print(self.data,end = ' ') #中
        if self.right: #右
            self.right.inorder_tree_walk()
    def tree_search(self,data):
        if self == None or self.data == data:
            return self

        if data < self.data:
            return self.left.tree_seatch(data)
        else :
            return self.right.tree_seatch(data)

    def iterative_tree_search(self,data):
        #非递归版查找一般会比递归版更快
        n = self
        while n != None and data != n.data:
            if data < n.data:
                n = n.left
            else:
                n = n.right
        return n

    def tree_mininum(self):
        if self.left:
            return self.left.tree_mininum()
        else:
            return self

    def tree_maximun(self):
        if self.right:
            return self.right.true_maximun()
        else:
            return self

    def tree_successor(self):
            
        """
        找后继：
        有右子树，取右子树中最小的
        没有右子树，也就是这个子树中最大的，应该向上找第一个把他当右子树的结点
        前驱 相反
        """
        x = self
        if x.right != None:
            return x.right.tree_mininum()
        else:
            p = x.parent
            while p and p.right == x:
                x = p
                p = p.parent
            return p
    def tree_predecessor(self):
        x = self
        if x.left != None:
            return x.left.tree_maximun()
        else:
            p = x.parent
            while p and p.left == x:
                x = p
                p = p.parent
            return p

    def tree_insert(self,data):
        #插入data
        node = self
        while node:
            if data < node.data:
                next = node.left
            else:
                next = node.right
            if next:
                node = next
            else:
                break
        nn = self.createNode(data)
        if data < node.data:
            node.left = nn
            node.left.parent = node
        else:
            node.right = nn
            node.right.parent = node
        return nn

    def tree_delete(self,root):
        '''
        root 中删除self
        1.没有子树直接删除
        2.有应该子树直接上移
        3.有2个只树 把后继拷贝到删除的结点
         '''
        n = self

        if n.left and n.right: #3
            s = n.right.tree_mininum()
            n.data = s.data
            root = s.tree_delete(root)
            return root

        if not n.parent: #根结点
            if n.left:
                root = n.left
                n.left = None
                root.parent = None
            elif n.right:
                root = n.right
                n.right = None
                root.parent = None
            else:
                root = None

            return root

        if not n.left and not n.right:
            if n.parent.left == n:
                n.parent.left = None
            else:
                n.parent.right = None
        else:
            if n.parent.left == n:
                n.parent.left = n.left or n.right
            else:
                n.parent.right = n.left or n.right
        n.patent = None
        return root

if __name__ == '__main__':
    root = Node(6)
    root.tree_insert(5)
    root.tree_insert(7)
    root.tree_insert(2)
    root.tree_insert(3)
    root.tree_insert(8)
    print("中序遍历: ",end = '')
    root.inorder_tree_walk()
    print("\n查找：",end = '')
    test1= root.iterative_tree_search(5)
    print(str(test1.data)+'的后继：'+str(test1.tree_successor().data))

    print("查找：",end = '')
    test2= root.tree_search(6)
    print(str(test2.data)+'的前驱：'+str(test2.tree_predecessor().data))
    test2.tree_delete(root)
    print("删除6后：",end = '')
    root.inorder_tree_walk()
    
'''
================= RESTART: F:\python\algorithms\12_1_tree.py =================
中序遍历: 2 3 5 6 7 8 
查找：5的后继：6
查找：6的前驱：5
删除6后：2 3 5 7 8

python 3.5.1 win7
'''

参考引用：

http://www.wutianqi.com/?cat=515&paged=4

http://blog.csdn.net/fxjtoday/article/details/6448083