关于过拟合、局部最小值、以及Poor Generalization的思考
Poor Generalization
这可能是实际中遇到的最多问题。
比如FC网络为什么效果比CNN差那么多啊,是不是陷入局部最小值啊?是不是过拟合啊?是不是欠拟合啊?
在操场跑步的时候,又从SVM角度思考了一下,我认为Poor Generalization属于过拟合范畴。
与我的论文 [深度神经网络在面部情感分析系统中的应用与改良] 的观点一致。
SVM
ImageNet 2012上出现了一个经典虐杀场景。见[知乎专栏]
里面有一段这么说道:
| 当时,大多数的研究小组还都在用传统computer vision算法的时候,多伦多大学的Hinton祭出deep net这样一个大杀器。差距是这样的: 第一名Deepnet的错误率是0.16422 |
除了Hinton组是用CNN之外,第二第三都是经典的SIFT+SVM的分离模型。
按照某些民科的观点,SVM是宇宙无敌的模型,结构风险最小化,全局最小值,那么为什么要绑个SIFT?
众所周知,SIFT是CV里最优良的Hand-Made特征,为什么需要这样的特征?
因为它是一种Encoding,复杂的图像经过它的Encoding之后,有一些很明显的性质(比如各种不变性)就会暴露出来。
经过Encoding的数据,分类起来是非常容易的。这也是模式识别的经典模式:先特征提取、再分类识别。
|
Question:如果用裸SVM跑ImageNet会怎么样?
My Answer:SVM的支持向量集会十分庞大。比如有10000个数据,那么就会有10000个支持向量。
|
SVM不同于NN的一个关键点就是,它的支持向量是动态的,虽然它等效于NN的隐层神经元,但是它服从结构风险最小化。
结构风险最小化会根据数据,动态算出需求最少的神经元(或者说是隐变量[Latent Variable])。
如果SVM本身很难去切分Hard数据,那么很显然支持向量会增多,因为[Train Criterion] 会认为这是明显的欠拟合。
欠拟合情况下,增加隐变量,增大VC维,是不违背结构风险最小化的。
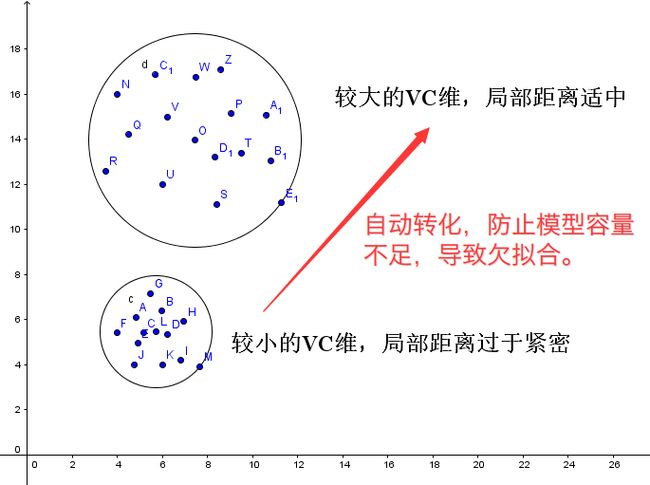
极限最坏情况就是,对每个点,拟合一个值,这样会导致最后的VC维无比庞大,但仍然满足结构风险最小化。图示如下:
之所以要调大VC维,是因为数据太紧密。
如果吃不下一个数据,那么找局部距离的时候,就会总是产生错误的结果。
尽管已经很大了,但是仍然需要更大,最好是每个点各占一个维度,这样100%不会分错。
这会导致另外一个情况发生:过拟合,以及维数灾难:
|
维数灾难:
在Test Phase,由于参数空间十分庞大,测试数据只要与训练数据有稍微变化,很容易发生误判。
原因是训练数据在参数空间里拟合得过于离散,在做最近局部距离评估时,各个维度上,误差尺度很大。测试数据的轻微变化就能造成毁灭级误判,学习的参数毫无鲁棒性。
|
不过,由于现代SVM的[Train Criterion] 一般含有L2 Regularier,所以可以尽力压制拟合的敏感度。
如果L2系数大点,对于大量分错的点,会全部视为噪声扔掉,把过拟合压成欠拟合。
如果L2系数小点,对于大量分错的点,会当成宝去拟合,虽然不至于维数灾难,过拟合也会很严重。
当然,一般L2的系数都不会压得太狠,所以过拟合可能性应当大于欠拟合。
我曾经碰到一个例子,我的导师拿了科大讯飞语音引擎转化的数据来训练SVM。
Train Error很美,Test Error惨不忍睹,他当时和我说,SVM过拟合好严重,让我换个模型试试。
后来我换了CNN和FC,效果也差不多。
从Bayesian Learning观点来讲,Model本身拥有的Prior并不能摸清训练数据Distribution。
这时候,无论你是SVM还是CNN,都是回天无力的,必然造成Poor Generalization。
不是说,你搞个大数据就行了,你的大数据有多大,PB级?根本不够。
单纯的拟合来模拟智能,倒更像是是一个NPC问题,搜遍全部可能的样本就好了。
悲剧的是,世界上都没有一片树叶是完全相同的,美国的PB级树叶的图像数据库可能根本无法解决中国的树叶问题。
也不是说,你随便套个模型就了事了,更有甚者,连SVM、NN都不用,认为机器学习只要LR就行了。
“LR即可解决湾区数据挖掘问题”,不得不说,无论是传播这种思维、还是接受这种思维的人,都是时代的悲哀。
NN
再来看一个NN的例子,我在[深度神经网络以及Pre-Training的理解]一文的最后,用了一个神奇的表格:
[FC]
| 负似然函数 | 1.69 | 1.55 | 1.49 | 1.44 | 1.32 | 1.25 | 1.16 | 1.07 | 1.05 | 1.00 |
| 验证集错误率 | 55% | 53% | 52% | 51% | 49% | 48% | 49% |
49% | 49% | 49% |
[CNN]
| 负似然函数 | 1.87 | 1.45 | 1.25 | 1.15 | 1.05 | 0.98 | 0.94 | 0.89 | 0.7 | 0.63 |
| 验证集错误率 | 55% | 50% | 44% | 43% | 38% | 37% | 35% |
34% | 32% | 31% |
当初只是想说明:FC网络的Generalization能力真是比CNN差太多。
但现在回顾一下,其实还有有趣的地方。
I、先看FC的Epoch情况,可以看到,后期的Train Likelihood进度缓慢,甚至基本不动。
此时并不能准确判断,到底是欠拟合还是陷入到局部最小值。
但,我们有一点可以肯定,增大FC网络的规模,应该是可以让Train Likelihood变低的。
起码在这点上,应该与SVM做一个同步,就算是过拟合,也要让Train Likelihood更好看。
II、相同Train Likelihood下,CNN的Test Error要低很多。
如果将两个模型看成是等效的规模(实际上CNN的规模要比FC低很多),此时FC网络可以直接被判为过拟合的。
这点需要转换参照物的坐标系,将CNN看作是静止的,将FC网络看作是运动的,那么FC网络Test Error就呈倒退状态。
与过拟合的情况非常类似。
综合(I)(II),个人认为,从相对运动角度,Poor Generalization也可以看作是一种过拟合。
(II)本身就很糟了,如果遇到(I)的情况,那么盲目扩张网络只会变本加厉。
这是为什么SVM过拟合非常可怕的原因,[知乎:为什么svm不会过拟合?]