数据结构图文解析之：二分查找及与其相关的几个问题解析

0. 数据结构图文解析系列

数据结构系列文章
数据结构图文解析之：数组、单链表、双链表介绍及C++模板实现
数据结构图文解析之：栈的简介及C++模板实现
数据结构图文解析之：队列详解与C++模板实现
数据结构图文解析之：树的简介及二叉排序树C++模板实现.
数据结构图文解析之：AVL树详解及C++模板实现
数据结构图文解析之：二叉堆详解及C++模板实现
数据结构图文解析之：哈夫曼树与哈夫曼编码详解及C++模板实现
数据结构图文解析之：直接插入排序及其优化（二分插入排序）解析及C++实现
数据结构图文解析之：二分查找及与其相关的几个问题解析

1. 二分查找简介

二分查找大家都不陌生，可以说除了最简单的顺序查找之外，我们第二个接触的查找算法就是二分查找了。顺序查找的时间复杂度是O(n)，二分查找的时间复杂度为O(logn)。在面试中二分查找被考察的概率还是比较高的，上次去面试时就遇到手写二分查找的题目。二分查找不难，但我们要能做到准确、快速地写出二分查找的代码，能对二分查找的效率做出分析，还能够将二分查找的思想来解决其他的问题。

1.1 二分查找过程图解

二分查找要求序列本身是有序的。因此对于无序的序列，我们要先对其进行排序。现在我们手头有一有序序列：
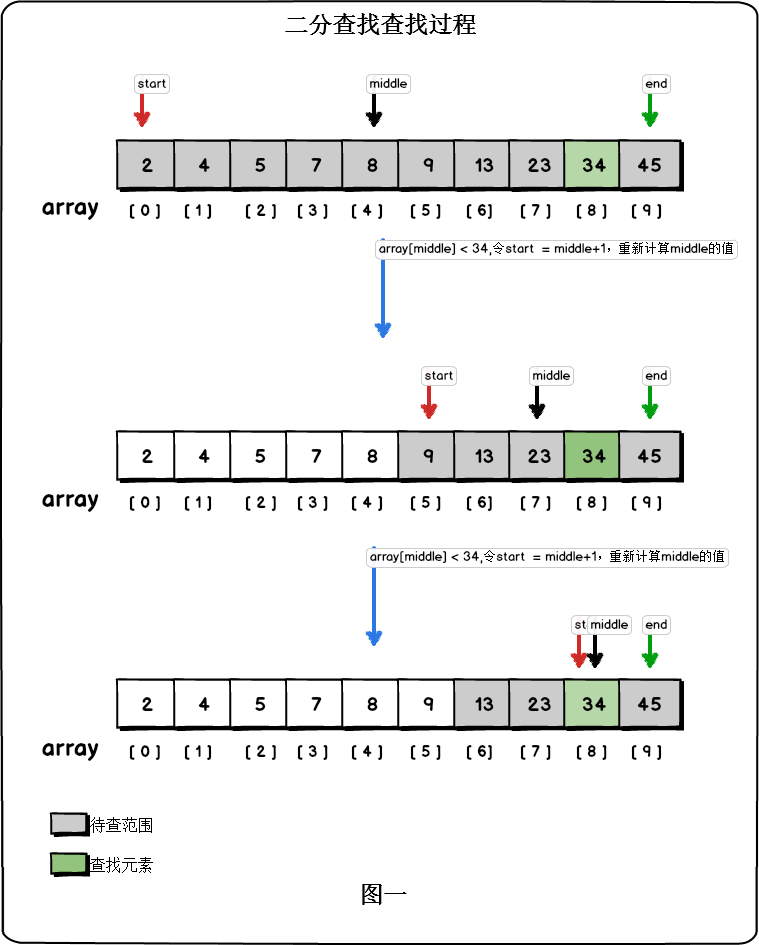
array[10] = {2,4,5,7,,8,9,13,23,34,45}，则二分查找的过程为：

• 设置三个索引：start指向数组待查范围的起始元素，end指向数组待查范围的最后一个元素，middle=(start+end)/2。开始时待查范围为整个数组。
• 比较array[middle]与查找元素的大小关系：
  • 如果array[middle]等于查找元素，则查找成功
  • 如果array[middle]大于查找元素，则说明待查元素在数组的前半部分，此时缩小待查范围，令end = middle-1
  • 如果array[middle]小于查找元素，则说明待查元素在数组的后半部分，此时缩小待查范围，令start = middle +1
• 重复执行前面两步，直到array[middle ] 等于查找元素则查找成功或start>end查找失败。

现在我们在数组{2,4,5,7,,8,9,13,23,34,45}中查找元素23，过程如图：

可见，每一次元素比较都可以把待查范围缩小1/2，因此二分查找的时间复杂度为o(logn)。

1.2 二分查找实现代码

二分查找代码简单，可以递归或迭代地实现。递归容易实现，代码简单，但待查元素数量巨大时，递归深度也随之增大(logn的关系)，应考虑是否会发生栈溢出。迭代的实现也不复杂，但我们力求准确简洁。

递归实现

//查找成功时返回查找元素在数组中的下标；查找失败时返回-1
template <typename T>
int BinarySearch(const T array[], int start, int end, const T& value)
{
    if (start>end)
        return -1;
    int middle = (start + end) / 2;
    if (array[middle] == value)
        return middle;
    if (array[middle] < value)
    {
        return BinarySearch(array, middle+1, end, value);
    }
    return BinarySearch(array, start, middle-1, value);
};

迭代实现

template <typename T>
int BinarySearch(const T array[], int start, int end, const T& value)
{
    int result = -1;
    while (start <= end)
    {
        int middle = (start + end) / 2;
        if (array[middle] == value)
        {
            result = middle;
            break;
        }
        if (array[middle] < value)
        {
            start = middle + 1;
        }
        else
            end = middle - 1;
    }
    return result;
}

测试

为了方便用户使用，我们定义一个接口：

//用户使用接口
template <typename T>
int BinarySearch(const T array[], int length, const T& value)
{
    if (array == nullptr || length <= 0)
        return -1;
    return BinarySearch(array, 0, length - 1, value);
}

使用实例：

int _tmain(int argc, _TCHAR* argv[])
{
    int array[10] = { 2, 4, 5, 7, 8, 9, 13, 23, 34, 45 };
    int i;
    while (cin >> i)
    {
        cout << BinarySearch(array, 10, i) << endl;
    }
    return 0;
}

2. 二分查找的应用

2.1 二分插入排序

这是对直接插入排序的一种优化策略，能够有效减少插入排序的比较次数。
直接插入排序的思路是对于无序序列的第一个元素，从后至前进行顺序查找 扫描有序序列寻找合适的插入点。改进后的二分插入排序算法使用二分查找在有序序列中查找插入点，将插入排序的比较次数降为O(log2n)。这个思路的实现代码为：

/*二分查找函数，返回插入下标*/
template <typename T>
int BinarySearch(T array[], int start, int end, T k)
{
    while (start <= end)
    {
        int middle = (start + end) / 2;
        int middleData = array[middle];
        if (middleData > k)
        {
            end = middle - 1;
        }
        else
            start = middle + 1;
    }
    return start;
}
//二叉查找插入排序
template <typename T>
void InsertSort(T array[], int length)
{
    if (array == nullptr || length < 0)
        return;
    int i, j;
    for (i = 1; i < length; i++)
    {
        if (array[i]<array[i - 1])
        {
            int temp = array[i];
            int insertIndex = BinarySearch(array, 0,i, array[i]);//使用二分查找在有序序列中进行查找，获取插入下标
            for (j = i - 1; j>=insertIndex; j--) //移动元素
            {
                array[j + 1] = array[j];  
            }      
            array[insertIndex] = temp;    //插入元素
        }
    }
}

若对插入排序不了解，可以看数据结构图文解析之：直接插入排序及其优化（二分插入排序）解析及C++实现。

2.2 旋转数组的最小数字问题

问题描述：把一个数组最开始的若干个元素搬到数组的末尾，我们称为数组的旋转，输入一个递增排序数组的一个旋转，输出旋转数组的最小元素。例如数组{4，5，6，1，2，3}为数组 {1，2，3，4，5，6}的一个旋转，最小旋转元素为1.

解决思路：
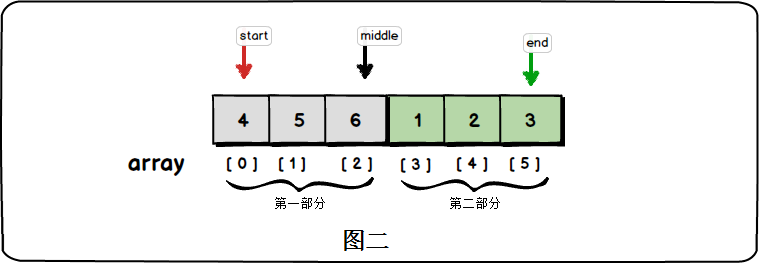
寻找数组中最小的元素，我们可以遍历数组，时间复杂度为O(n)。但是借助二分查找的思想，我们能够在O（logn）的时间复杂度内找到最小的元素。旋转数组的特点是数组中两个部分都分别是有序的，以{4，5，6，1，2，3}为例，{4，5，6}是非递减的，{1，2，3}也是非递减的：

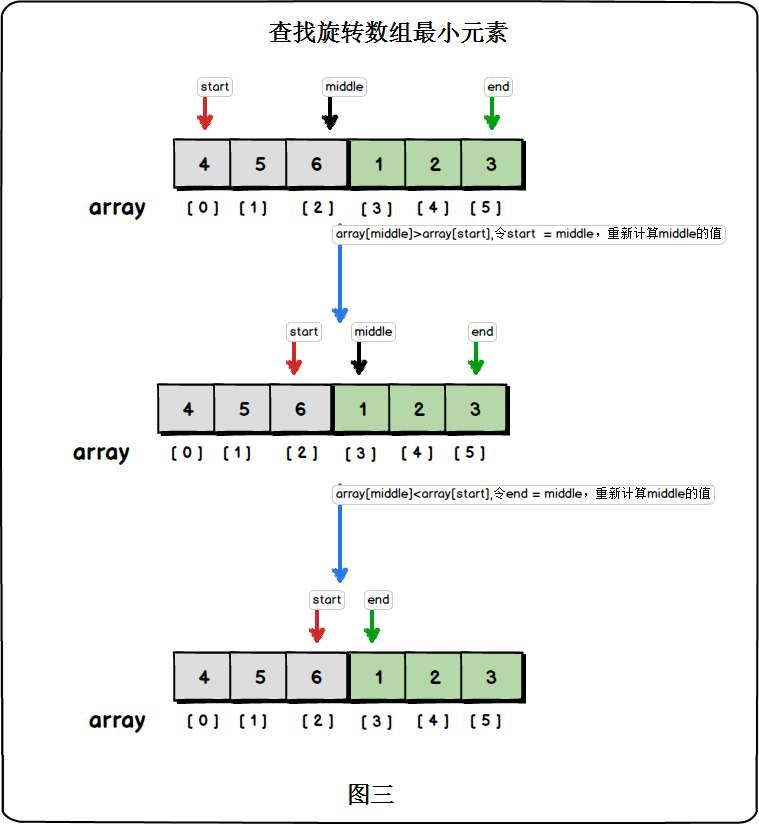
我们可以定义两个索引：start指向第一部分的起始位置；end指向第二部分的最后一个元素，如图所示。由于数组在旋转前整体有序，故array[start]>=array[end]，而中间值array[middle]满足：

• 如果array[middle]>array[start] ,则array[middle]属于第一部分。此时令start= middle ；
• 如果array[middle]<array[start] ,则array[middle]属于第二部分。此时令end = middle ；

循环执行上述操作，当start与end相邻时，end所指便是数组中的最小元素：

end所指元素便是最小元素。
这个寻址的过程有一个隐喻的要求:中间这个元素必须能够判断它是属于第一部分还是第二部分。在有些输入下，这个要求不能满足，例如数组：{0,1,1,1,1},它的两个选择数组为：

• {1,0,1,1,1}
• {1,1,1,0,1}

此时因array[middle] == array[start] == array[end] 而无法判断array[middle]属于哪一部分，我们只能进行顺序查找找出最小元素。

如图：

此时无法确定array[middle]是属于第一部分还是第二部分，这种情况下我们需要进行顺序查找。
因此，我们的代码实现为：

//顺序查找函数
int Min(int array[], int length)
{
    int result = array[0];
    for (int i = 1; i < length; i++)
    {
        if (array[i] < result)
            result = array[i];
    }
    return result;
}
 
int MinInRotation(int array[],int length)
{
    int result = -999;
    if (array == nullptr || length < 0)
        return result;
    int start = 0;
    int end = length - 1;
    int middle = start;
    while (start < end)
    {
        if (start + 1 == end)
        {
            result = array[end];
            break;
        }
        middle = (start + end)/2;
        //如果遇上特殊情况，则需要进行顺序查找
        if (array[middle] == array[start] && array[middle] == array[end])
            return Min(array,length); //调用顺序查找函数
        //否则；中间元素属于第一部分
        if (array[middle]>=array[start])
        {
            start = middle;
        }//中间元素属于第二部分
        else if (array[middle] <= array[start])
        {
            end = middle;
        }
    }
    return result;
}

测试代码：

int _tmain(int argc, _TCHAR* argv[])
{
    int array1[6] = { 4, 5, 6, 1, 2, 3 };
    int array2[5] = { 1, 0, 1, 1, 1 };
    int array3[5] = { 1, 1, 1, 0, 1 };
    cout << MinInRotation(array1, 6)<<endl;
    cout << MinInRotation(array2, 5) << endl;
    cout << MinInRotation(array3, 5) << endl;
 
    getchar();
    return 0;
}

运行结果：

1
0
0

2.3 数字在排序数组中出现次数问题

问题描述：统计一个数组在排序数组中出现的次数。例如输入排序数组{1，2，3，3，3，3，4，5}和数字3，由于3在数组中出现了4次，因此输出4.

解决思路：假设我们是统计数字k在排序数组中出现的次数，只要找出排序数组中第一个k与最后一个k的下标，就能够计算出k的出现次数。
寻找第一个k时，利用二分查找的思想，我们总是拿k与数组的中间元素进行比较。如果中间元素比k大，那么第一个k只有可能出现在数组的前半段；如果中间元素等于k，我们就需要判断k是否是前半段的第一个k，如果k前面的元素不等于k，那么说明这是第一个k；如果k前面的元素依旧是k，那么说明第一个k在数组的前半段中，我们要继续递归查找。

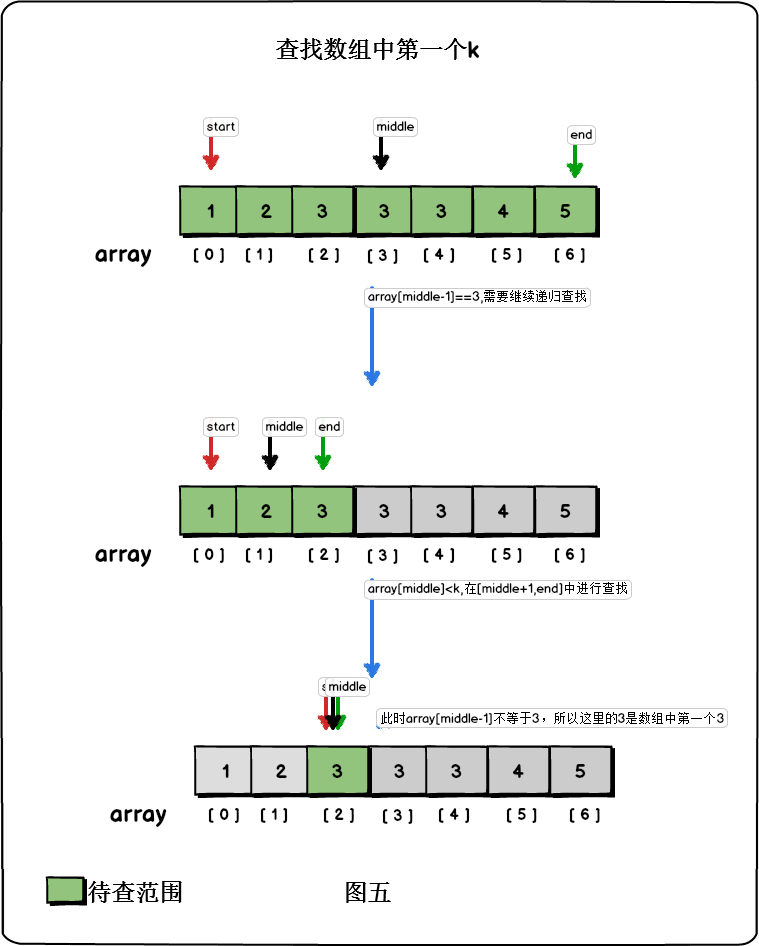
这个过程的代码：

int getFirstIndex(int array[], int start ,int end, int k)
{
    if (start > end)
        return -1;
    int middle = (start + end) / 2;
    int middleData = array[middle];
    if (middleData == k)
    {
        if (middle == 0 || array[middle - 1] != k)
            return middle;
        else
            end = middle - 1;
    }
    else if (middleData>k)
    {
        end = middle - 1;
    }
    else
        start = middle + 1;
    return getFirstIndex(array, start, end, k);
}

同样的思路，我们在数组中寻找最后一个k，如果中间元素比K大，那么k只能出现在数组的后半段；如果中间元素比K小，那么K只能出现在数组的前半段。如果中间元素等于k，而k后面的元素等于k，那么最后一个k只能在后半段出现；否则k为数组中最后的一个k。

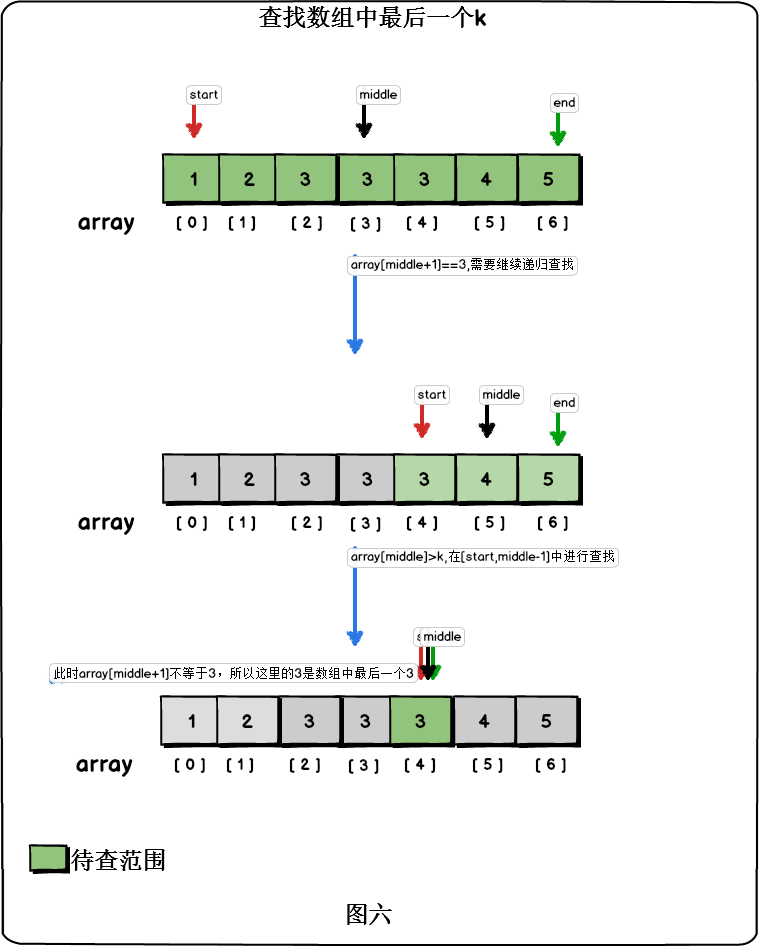
代码如下：

///获取最后一个K的下标
int getLastIndex(int array[], int start,int end,int length, int k)
{
    if (start > end)
        return -1;
    int middle = (start + end) / 2;
    int middleData = array[middle];
    if (middleData == k)
    {
        if (middle == length-1 || array[middle+ 1] != k) //最后一个k
            return middle;
        else
            start = middle + 1;
    }
    else if (middleData>k)
    {
        end = middle - 1;
    }
    else
        start = middle + 1;
    return getLastIndex(array, start, end,length, k);
}

把第一个坐标与最后一个坐标算出来后，我们可以进行元素出现次数的计算：

//计算元素出现个数
int CountKInArray(int array[], int length, int k)
{
    int result=-1;
    if (array != nullptr && length > 0)
    {
        int firstPos = getFirstIndex(array, 0, length - 1, k);
        int lastPos = getLastIndex(array, 0, length - 1, length, k);
        if (firstPos != -1 && lastPos != -1)
        {
            result = lastPos - firstPos+1;
        }
    }
    return result;
}

测试：

int _tmain(int argc, _TCHAR* argv[])
{
    int array[8] = { 1, 2, 3, 3, 3, 4, 5 };
 
    cout << "数组array中数字3出现的次数为："<<CountKInArray(array, 7, 3) << endl;
    getchar();
    return 0;
}

运行结果：

数组array中数字3出现的次数为：3

原创文章，转载请注明：http://www.cnblogs.com/QG-whz/p/5194627.html