“压缩感知” 之 “Hello World”

上一篇《压缩感知进阶——有关稀疏矩阵》中我们已经讲过了压缩感知原理、应用领域、可行性以及恢复信号机制，后面有朋友陆续反应希望有一个CS版Helloworld，这里我就借用香港大学沙威大牛的一个程序在代码层面对CS做一讲解。

Keywords: 压缩感知 compressive sensing, 稀疏（Sparsity）、不相关（Incoherence）、随机性（Randomness）

先给出Code：

%  1-D信号压缩传感的实现(正交匹配追踪法Orthogonal Matching Pursuit)
%  测量数M>=K*log(N/K),K是稀疏度,N信号长度,可以近乎完全重构
%  编程人--香港大学电子工程系 沙威  Email: [email protected]
%  编程时间：2008年11月18日
%  文档下载: http://www.eee.hku.hk/~wsha/Freecode/freecode.htm 
%  参考文献：Joel A. Tropp and Anna C. Gilbert 
%  Signal Recovery From Random Measurements Via Orthogonal Matching
%  Pursuit，IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 12,
%  DECEMBER 2007.

clc;clear

%%  1. 时域测试信号生成
K=7;      %  稀疏度(做FFT可以看出来)
N=256;    %  信号长度
M=64;     %  测量数(M>=K*log(N/K),至少40,但有出错的概率)
f1=50;    %  信号频率1
f2=100;   %  信号频率2
f3=200;   %  信号频率3
f4=400;   %  信号频率4
fs=800;   %  采样频率
ts=1/fs;  %  采样间隔
Ts=1:N;   %  采样序列
x=0.3*cos(2*pi*f1*Ts*ts)+0.6*cos(2*pi*f2*Ts*ts)+0.1*cos(2*pi*f3*Ts*ts)+0.9*cos(2*pi*f4*Ts*ts);  %  完整信号,由4个信号叠加而来

%%  2.  时域信号压缩传感
Phi=randn(M,N);                                   %  测量矩阵(高斯分布白噪声)64*256的扁矩阵，Phi也就是文中说的D矩阵
s=Phi*x.';                                        %  获得线性测量 ，s相当于文中的y矩阵

%%  3.  正交匹配追踪法重构信号(本质上是L_1范数最优化问题)
%匹配追踪：找到一个其标记看上去与收集到的数据相关的小波；在数据中去除这个标记的所有印迹；不断重复直到我们能用小波标记“解释”收集到的所有数据。

m=2*K;                                            %  算法迭代次数(m>=K)，设x是K-sparse的
Psi=fft(eye(N,N))/sqrt(N);                        %  傅里叶正变换矩阵
T=Phi*Psi';                                       %  恢复矩阵(测量矩阵*正交反变换矩阵)

hat_y=zeros(1,N);                                 %  待重构的谱域(变换域)向量                     
Aug_t=[];                                         %  增量矩阵(初始值为空矩阵)
r_n=s;                                            %  残差值

for times=1:m;                                    %  迭代次数(有噪声的情况下,该迭代次数为K)
    for col=1:N;                                  %  恢复矩阵的所有列向量
        product(col)=abs(T(:,col)'*r_n);          %  恢复矩阵的列向量和残差的投影系数(内积值) 
    end
    [val,pos]=max(product);                       %  最大投影系数对应的位置，即找到一个其标记看上去与收集到的数据相关的小波
    Aug_t=[Aug_t,T(:,pos)];                       %  矩阵扩充    
    
    T(:,pos)=zeros(M,1);                          %  选中的列置零（实质上应该去掉，为了简单我把它置零），在数据中去除这个标记的所有印迹
    aug_y=(Aug_t'*Aug_t)^(-1)*Aug_t'*s;           %  最小二乘,使残差最小
    r_n=s-Aug_t*aug_y;                            %  残差
    pos_array(times)=pos;                         %  纪录最大投影系数的位置
end
hat_y(pos_array)=aug_y;                           %  重构的谱域向量
hat_x=real(Psi'*hat_y.');                         %  做逆傅里叶变换重构得到时域信号

%%  4.  恢复信号和原始信号对比
figure(1);
hold on;
plot(hat_x,'k.-')                                 %  重建信号
plot(x,'r')                                       %  原始信号
legend('Recovery','Original')
norm(hat_x.'-x)/norm(x)                           %  重构误差

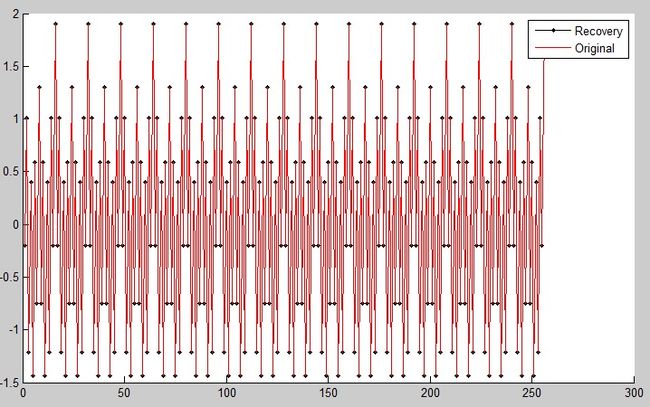
程序运行结果:

其中红色是原信号，黑色是恢复后的信号，可见利用压缩感知的恢复情况非常好。

具体讲解和原理我在下面写了，由于csdn中公式真心不好写，我只能用手写了，请大家见谅。

关于压缩感知的原理请详见上一篇文章《压缩感知进阶——有关稀疏矩阵》和《初始压缩感知——Compressive Sensing》。

关于Compressive Sensing更多的学习资料将继续更新，敬请关注本博客和新浪微博Rachel____Zhang。