Persistent Ideal Hash Tries---一种Java实现

最近看关于clojure的资料，从rich Hickey（clojure的创造者）的《Persistent Data Structure and Managed Reference》中看到了关于ideal hash trees的介绍，于是找到了Phil Bagwell关于"ideal hash trees"的论文，研究了一下，并结合rich Hickey关于Persistent Ideal Hash Trees的介绍，用Java实现了一个Persistent Ideal Hash Trees（两杯咖啡加一个下午，希望不会有太多的bug），下面就是对该数据结构的简单介绍和我的实现细节，供参考。

Ideal Hash Trees

Ideal Hash Trees可以看作是树和哈希表的组合，融合了树和哈希表的优势，当然也有缺点，但主要还是优点。
跟哈希表相比，Ideal Hash Trees在扩展和收缩上非常方便，当一个哈希表需要扩容时，通常你需要重新分配一个双倍的哈希表，然后将原来的数据re-hash到新的哈希表中，这导致了很大的代价，而Ideal Hash Trees由于是树，很容易扩展，只需要向下层扩展分支；而对于稀疏哈希表，会存在大量的空间浪费，如果你想压缩它，也需要大量的操作，但Ideal Hash Trees则只需要很小的代价，将空闲的分支节点移除就可回收空间；并且在使用哈希表时，你往往需要让占用保持在60%或者70%以下，以保持效率，但在Ideal Hash Trees中则不需要，只需要保持较少的空闲空间。因此，Ideal Hash Trees相比传统的哈希表更容易扩展和收缩，只需要较少的多余空间，具有很大的优势。
在查询效率上，哈希表的SET和GET的时间复杂度是1，一次哈希值的计算加一次比对（在存在哈希冲突的情况下，也许需要多次比对），而Ideal Hash Trees则需要更多，具有32个分支数的Ideal Hash Trees最大高度是6，但由于一个4层的Ideal Hash Trees就可以容纳上百万条数据，因此Ideal Hash Trees查询的时间复杂度通常小于6，可以认为是一个常数，和哈希表非常接近。
你可以把Ideal Hash Trees每个节点的都看成一个小规模的哈希表，当出现哈希冲突时，就向下层扩展，直到不再冲突，或者，在到达最后一层后任然存在哈希冲突（虽然我们应该尽量避免这种情况，但有时候是无法避免的），这时，我们就需要使用一些解决哈希冲突的办法，例如，使用链表。
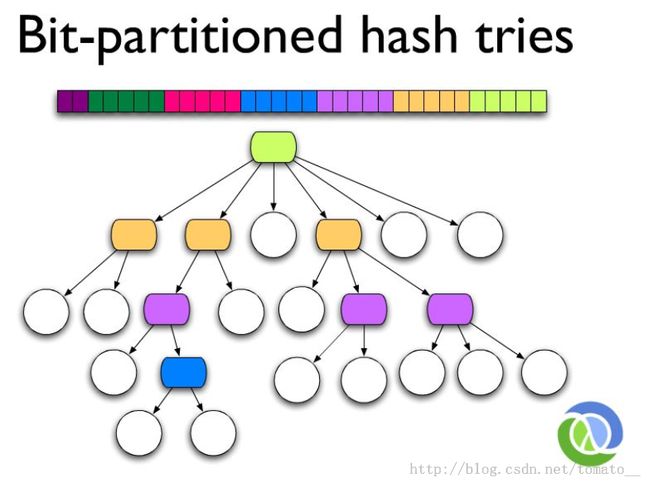
下面是Ideal Hash Trees的一个示例（来自《Persistent Data Structure And Managed Reference》）:

下面我们来看看Ideal Hash Trees的主要操作：

查找

当通过一个Key进行查找时，计算Key的哈希值keyHashValue，通常是一个32位的整数。首先，取keyHashValue开始的5位（或者你认为最有意义的5位）作为整数L1，取root的第L1个孩子，即root.children[L1]，如果root.children[L1]是叶子节点，匹配则返回，否则返回失败，如果root.children[L1]是中间节点，则取keyHashValue的下5位作为整数L2，得到root.children[L1].children[L2]，重复上面的步骤，依次向下，直到到达叶子节点，若匹配成功，则返回，否则返回失败。
由于Ideal Hash Trees的层次很少，最多6层，因此只需要少量的计算和一次比对（不考虑存在哈希冲突）即查找完成。

插入

插入的节点分为两个部分：key和value。计算key的哈希值keyHashValue，同样，取keyHashValue开始的5位（或者你认为最有意义的5位）作为整数L1，若root.children[L1]为空，则将插入的value作为root.children[L1]，插入完成，否则将出现两种情况：
1）root.children[L1]不为空，是一个中间节点，则取keyHashValue的下5位作为整数L2，得到root.children[L1].children[L2]，进入下一层的重复上面的操作；
2）root.children[L1]不为空，且是一个叶子节点，则表示出现了哈希冲突，则需要将root.children[L1]替换为一个中间节点，并将原来的root.children[L1]先插入中间节点的下一层，value的插入也在下一层重复上面的操作。
按照以上步骤，如果一直到最后一层（第6层）任然存在哈希冲突，则需要解决冲突，我采用链表的方式来解决哈希冲突。

删除和修改

删除和修改操作都可以对应到查找操作，即首先需要通过key找到对应的节点，然后执行操作。不同的是删除只需要传入key，而修改则需要key和value。
值得高兴的是Ideal Hash Trees不像红黑树一样，需要维护树的平衡性，但节点删除后任然需要考虑空节点的回收，当一个节点的所有子节点都为空后，就需要回收掉。

Persistent Ideal Hash Tries

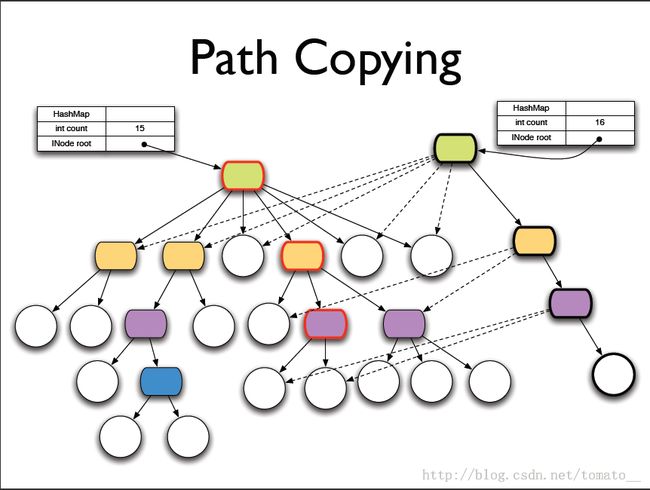
Persistent Ideal Hash Tries是在Ideal Hash Trees上的改进，它采用一种基于树的copy-on-write方法，保证了多线程安全性。当一个节点发生改变时，就将该节点和该节点的路径上的节点拷贝出来（由于数据不会发生变化，因此只需要做浅拷贝），不影响原有的数据，最后通过替换根节点来更新整棵树，见下图（来自《Persistent Data Structure And Managed Reference》）：

Persistent Ideal Hash Tries的修改不会导致原有数据的改变，因此修改操作不会阻塞查询操作。但如果同一时间存在多个线程修改数据，则多个线程的修改就会导致冲突，这样其中一个线程的操作成功后，其它的线程的操作就需要重做，因此Persistent Ideal Hash Tries在写少读多的应用中会表现的更好。下面我们来看看具体的实现。

实现

我使用Java来实现Persistent Ideal Hash Tries，这里是一个C++的实现" Ideal Hash Tries: an implementation in C++"，有兴趣的同学可以看看。

常量和根节点定义

public class PersistentIdealHashTree<K, V> {
	//定义分支个数
	private static final int CHILD_COUNT = 32;
	//定义最大层，也可以通过分支个数来计算这里我直接写死了
	private static final int MAX_LAYER = 6;
	//定义根节点，使用一个原子变量，这里也是整棵树发生变化的地方
	private final AtomicReference<TreeNode> root;

	public PersistentIdealHashTree() {
		this.root = new AtomicReference<TreeNode>(new TreeNode(null, CHILD_COUNT));
	}
	......
}

树节点

private class TreeNode {
	//节点数据链表
	private final NodeData data;
	//孩子节点，如果为叶子节点，则是一个0长度数组
	private final TreeNode[] children;

	@SuppressWarnings("unchecked")
	public TreeNode(NodeData data, int childCount) {
		this.data = data;
		this.children = new PersistentIdealHashTree.TreeNode[childCount];
	}
	......
}
private class NodeData {
	//数据key
	private final K key;
	//用户数据
	private final V userObj;
	//下一个节点指针
	private NodeData next;

	public NodeData(K key, V userObj, NodeData next) {
		this.key = key;
		this.userObj = userObj;
		this.next = next;
	}
}

用户数据之所以使用链表，主要是由于可能存在哈希冲突，在一个设计良好的系统中，确认不存在哈希冲突的情况下，也可以改为使用单个节点，可以简化操作和减少内存占用。

插入

public void insert(K key, V userObj) {
	boolean success = false;
	while (!success) {
		TreeNode oldRootNode = root.get();
		//insertNode将生成一棵新的树，返回根节点，不会修改原有的树
		TreeNode newRootNode = insertNode(oldRootNode, 1, key.hashCode(), key, userObj);
		//使用原子操作比较并替换老根节点，如果老根节点发生变化，则会失败，导致重做所有操作
		success = root.compareAndSet(oldRootNode, newRootNode);
	}
}

insertNode是具体插入节点的方法，它会返回一颗插入节点后的新的树根，然后替换老的根节点，如果老的根节点已经发生了变化，则一切就需要重做，直到成功。

private TreeNode insertNode(TreeNode parent, int layer, int keyHashCode, K key, V userObj) {
	//获取到插入节点在这层中的位置
	int position = getNodePosition(layer, keyHashCode);
	//拷贝一个新的parent节点，只做浅拷贝
	TreeNode newParent = cloneTreeNode(parent);
	if (parent.children.length == 0 || parent.children[position] == null) {
		// parent是叶子节点，或者插入节点的位置为空，就构造一个新的叶子节点，并插入newParent的对应位置
		newParent.children[position] = createTreeLeafNode(key, userObj, null);
	} else if (parent.children[position].data == null) {
		// parent是中间节点，则进入下一层操作
		newParent.children[position] = insertNode(parent.children[position], layer + 1, keyHashCode, key, userObj);
	} else {
		//出现哈希冲突
		if (layer < MAX_LAYER) {
			//由于树还可以继续向下扩展，于是将现在的节点替换为一个中间节点后，进入下一层
			TreeNode newChild = CreateTreeParentNode();
			newChild.children[getNodePosition(layer + 1, parent.children[position].data.key.hashCode())] = parent.children[position];
			newParent.children[position] = insertNode(newChild, layer + 1, keyHashCode, key, userObj);
		} else {
			//树已经不能再向下扩展，将插入的节点放入叶子节点的值链表中
			newParent.children[position] = createTreeLeafNode(key, userObj, parent.children[position]);
		}
	}
	return newParent;
}

查找

public V get(K key) {
	return getNode(root.get(), 1, key.hashCode(), key);
}

查找没有任何的阻塞操作，由于根节点是不会变化的，因此这里获取到的根节点相当于此时的树的一个快照，因此在查找的过程中即使数据已经发生变化，任然会查找到此时快照中的对应节点。

private V getNode(TreeNode parent, int layer, int keyHashCode, K key) {
	int position = getNodePosition(layer, keyHashCode);
	if (parent.children.length > 0 && parent.children[position] != null) {
		if (parent.children[position].data == null) {
			//中间节点，继续向下查找
			return getNode(parent.children[position], layer + 1, keyHashCode, key);
		} else {
			// 由于可能存在冲突，因此使用一个循环处理
			NodeData data = parent.children[position].data;
			do {
				if (data.key.equals(key)) {
					return data.userObj;
				}
				data = data.next;
			} while (data != null);
		}
	}
	return null;
}

修改和删除

修改和删除类似，都是首先找到对应节点，然后执行修改或者删除操作，操作的过程和插入类似，也是需要拷贝整个变化的路径，然后在根节点执行替换，需要注意的是，删除需要回收空节点。下面只介绍删除操作：

public V delete(K key) {
	boolean success = false;
	V userObj = null;
	while (!success) {
		TreeNode oldRootNode = root.get();
		//确认是否存在删除的数据，存在则执行删除操作
		userObj = getNode(oldRootNode, 1, key.hashCode(), key);
		if (userObj != null) {
			//执行删除操作，返回一个新的root，由于节点回收，可能返回空，这时需要构造一个空的新root
			TreeNode newRootNode = deleteNode(oldRootNode, 1, key.hashCode(), key);
			if (newRootNode == null) {
				newRootNode = CreateTreeParentNode();
			}
			//老的root已经发生变化，需要重做
			success = root.compareAndSet(oldRootNode, newRootNode);
		} else {
			success = true;
		}
	}
	return userObj;
}

删除操作主要的流程就是多了一次查找，而在deleteNode中，由于已经确认数据存在，就不再需要做数据是否存在的判断了：

private TreeNode deleteNode(TreeNode parent, int layer, int keyHashCode, K key) {
	int position = getNodePosition(layer, keyHashCode);
	TreeNode newParent = cloneTreeNode(parent);
	if (parent.children[position].data == null) {
		//中间节点，进入下一层操作
		newParent.children[position] = deleteNode(parent.children[position], layer + 1, keyHashCode, key);
	} else {
		//可能存在哈希冲突，在修改链表时采用copy-on-write方法，不改变原有链表
		NodeData data = parent.children[position].data;
		Stack<NodeData> dataStack = new Stack<>();
		while (data != null && !data.key.equals(key)) {
			dataStack.push(data);
			data = data.next;
		}
		NodeData rootData = data.next;
		while (!dataStack.empty()) {
			data = dataStack.pop();
			rootData = new NodeData(data.key, data.userObj, rootData);
		}
		TreeNode newNode = null;
		if (rootData != null) {
			newNode = new TreeNode(rootData, 0);
		}
		newParent.children[position] = newNode;
	}
	//newParent的所有孩子都为空后就可以回收了
	return newParent.isNullNode() ? null : newParent;
}

性能

Persistent Ideal Hash Tries具有较少的层次，操作的时间复杂度很低，是一个常量，具体的分析参考Phil Bagwell的论文，这里我给出在我的机器上的测试数据供大家参考。

测试环境

处理器：intel(R) Core(TM) i5-2400 CPU @3.10GHz 3.10GHz
内存：4.00GB(3.17GB可用)
系统：32为Win7
编译和执行环境：JDK1.7、eclipse
由于机器安装了太多应用，测试数据只能做个参考。

测试结果

1）插入
插入100万条数据（单位ms）：
单线程：2490
2个线程：2738
3个线程：2679
4个线程：3033
6个线程：3192
8个线程：2995
16个线程：3267
在线程数量增加后，由于存在冲突，因此插入效率降低，从测试结果可见使用单线程插入效果是最好的。
2）查询
读取200万数据耗时605ms。
3）删除
删除100万数据花费1611ms。


介绍就到这里了，希望能够对你有所帮助，如果存在问题，可以给我留言，谢谢。
你能从我的资源中下载所有源代码，发现bug或者你有更好的实现方法麻烦给我留言，非常感谢。