[置顶] 算法实习生学习之路--UCB算法

前言：

      来万物花开这家创业公司实习，也真是一波三折。先实习了三天，每天下午到公司工作到晚上。工作时间是每天下午到晚上9.30。结果每天上午没法用心干实验室的活了，下午在公司工作的时候，总是提心吊胆，手机震动一下就会立刻拿出来看看是不是老师找我了。这样的日子感觉没法持续下去，想找导师谈谈之前，就从实验室同学那儿知道了老师对我最近的出勤率太低很不高兴。想着还是找找导师谈一谈实习的问题吧，然后还在犹豫的时候，大boss就找我谈话了，退学or干活。于是只能拒绝了实习，安心回实验室吧。

意外的是，创业公司带我的老大陈开江师兄念在是北理工的同门师兄弟上，加上我对于转互联网方向的决心强烈，决定给我一个机会，每周一到周五晚上干活，周末拿一天时间出来交流，就算我实习三天了。只能说太感谢陈开江师兄了，让我在这么恶劣的条件下还给我实习的机会。

我的github：

我实现的代码全部贴在我的github中，欢迎大家去参观。

在作为算法实习生时，所实现的代码产权应该属于公司，所以在github中公布的代码可能会缺少一部分，或者比较简单，不涉及业务。

https://github.com/YinWenAtBIT

算法介绍：

背景介绍：

一、问题模型：

Multi-armed bandit问题，中文译名或叫做“多臂赌博机”问题。

在概率论中，多臂赌博机问题（有时也称为K臂/N臂赌博机问题），是一个赌徒需要在一排老虎机前决定拉动哪一个老虎机的臂，并且决定每个臂需要被拉动多少次的问题。每台老虎机提供的奖励是与它自身的奖励随机分布的函数相关的。赌徒的目标是最大限度地通过杠杆拉动序列，使得获得的奖励最大化。

在实际应用中，多臂模型被用来模拟管理研究项目，比如一家制药公司，要给定一个的预算，问题是在各个项目中分配资源，项目的回报暂时只知道一部分，需要在项目进行的过程中才会知道的越来越清楚。

因此，在解决这个问题的时候，需要在“exploration”（探索新臂以获得跟多关于臂的回报的信息）和“exploitation”（选择已有回报最高的臂来获取最大利益）之中进行权衡。

数学模型：

多个臂的回报可以看做是一组真实的随机分布，，K代表臂杆。代表每个臂的平均回报，赌徒每一轮拉下一个臂，并得到一次回报，是剩余可玩的轮数。多臂问题等同于一个状态的马尔科夫问题。轮之后的后悔度为，可用如下公式表示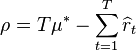：，其中是最大回报的平均数，，是在t时获得的回报。

一个零后悔度的策略会使得在无限次选择臂杆后以概率1趋近与0。那么，零后悔策略将在玩了足够多次之后趋近与最优策略。

UCB1算法：

UCB – The Upper Confidence BoundAlgorithm，上置信算法

小量贪婪算法和SOFTMAX算法缺陷：

前面所提及的算法（《Bandit Algorithms for Website Optimization》一书的前几章所介绍的算法，这里我直接拿它总结的结果使用）有一个弱点，它们只关心回报是多少，并不关心每个臂被拉下了多少次，这就意味着，这些算法不再会选中初始回报特别低臂，即使这个臂的回报只测试了一次。使用UCB1算法，将会不仅仅关注于回报，同样会关注每个臂被探索的次数。

在介绍UCB1算法之前，先总结一下前几章的介绍的epsilon-Greedy and Softmax algorithms（小量贪婪算法和SOFTMAX算法）的特点：

1.默认选择当前已知的回报率最高的臂杆

2.偶尔选择那些没有最高回报的臂杆

——小量贪婪算法随机选择，这样其他每个臂被选中的概率很小；

——SOFTMAX算法根据回报率选择臂杆，回报率比最大值小很多的臂杆很少选中，回报率接近最大值的笔杆被选中的概率接近最大臂被选中的概率

为了让这两种算法表现更好，我们可以在运行过程中动态的修改它们的参数，这种方式叫做退火算法。

我们需要知道每个臂的回报的置信度是因为，我们得到的每一个臂的回报结果是随机的，其中含有噪声。臂A看起来似乎比臂B选择要好，只有我们得到了足够多的数据，这时我们才能确认臂A优于臂B。

其他两种算法是容易被误导的，初始遇上了一次随机坏的结果，会把这个结果当做这个臂的回报。UCB算法不会受到臂回报随机性的影响。

因此，在实现UCB算法时，我们需要记录下对每个臂回报的置信度，做法是记录下每个臂被选择了多少次。

UCB1算法特性：

在实现UCB算法的时候，我们不需要关心其他的假设条件，只要满足一个条件：回报是分布在0-1之间，1代表最大的回报。如果使用的模型最大回报结果超出了这个范围，需要对结果进行归一化。

除了保存每个臂结果的置信度以外，UCB算法还在以下两个点不同与之前的算法：

1. UCB完全不使用随机性，每一种情况下，UCB选择的臂都是可以通过数据计算出来的

2. UCB算法没有任何需要配置的参数，这意味着，在任何情况下你都可以使用UCB算法，没有任何需要的先验条件

UCB算法实现：

每个臂包含的数据：

struct UCBNode
{
	int counts;
	double values;
};

UCB类成员：

class UCB1
{
public:
	UCB1();
	~UCB1();
	bool update(string & key, double res);
   	bool update(const char *startPos, double res);
   	string toString();
	bool readFromString(const string& JString);
	string select_arm();
	std::vector<std::string> & select_arm_N(size_t n);
	std::vector<std::string> keystrs;
private:
	insert(string & key, UCB value);
	std::unordered_map<string, UCB> frequencyReward; 
	int totalcount;
};

选择臂：

UCB算法选择臂算法如下：

1. 如果有counts为0的臂，即从未被选择的臂，那么先选择它（即初始时每个臂都会被选择一次）

2. 如果所有臂都被选择过，则计算每个臂的bonus和value的和，bonus计算公式如下：

bonus = sqrt((2 *total_counts) / float(counts);

3.选择其中bonus加value值最大臂

string UCB1::select_arm()
{
	string maxkey;

	double bonus;
	double maxvalue = 0.0;

	if(frequencyReward.empty())
	throw empty_arm("no arm in the map");

	for(auto it = frequencyReward.begin(); it != frequencyReward.end(); it++ )
	{
		if(it->second.counts == 0)
			return it->first;
		
		bonus = sqrt(2* log((double)totalcount))/it->second.counts;
		if(maxvalue < bonus + it->second.values)
		{
			maxvalue = bonus + it->second.values;
			maxkey = it->first;
		}
	}

	return maxkey;
}

因为每一个臂都需要至少被选择一次，因此，在使用UCB算法时需要注意，如果选择的次数M小于总的臂数N，就要谨慎使用UCB算法了。

bonus的意义在于，如果我们对一个臂的了解过于少，因此它的value值在此时的置信度是很低的，所以我们需要选择这个臂来获取更多的信息。因此，bonus可以当做一个测量对臂了解多少的指标，了解越少，bonus越大。加入了bonus这个指标，我们可以说这个算法是有好奇心的，当对于一个臂的了解少于了下限，它会被选中，即使这个臂的回报率很低。

更新臂：

每一个臂被选中之后，会返回一个value，那么更新的方法如下：

1.该臂的counts成员数加一

2. 该臂的value变为：原有的value值和新返回的结果value值按比例相加

values = values*(n-1)/n + res/n;

验证UCB算法：

当我们使用UCB算法，它会以怎样的频率来选中最优的臂？答案在最开始时，所有的臂的置信度都很低，因此每个臂都会被选中几次，此时选中最优臂的概率不高，当已经选择了很多次时，每个臂的置信度都已经相当高了，此时会一直选择最优臂，偶尔选择其他置信度过低的臂。如下图所示

UCB算法与其他算法对比：

这里，我们使用退火版本的小量贪婪算法和Softmax算法与UCB1算法对比，一共有5个臂供选择。

首先是选中最优臂的概率:

可以明显看到，UCB1算法的波动明显高于其他两个算法。不过在模拟末尾处，UCB算法已经追上了其他的两个算法，如果模拟的次数跟多，UCB算法将会优于其他两个算法。

然后是平均的回报率：

UCB算法能很快找到最优的臂，不过优于为了提高每一个臂的置信度，它回去选择那些回报率不高的臂，因此收敛于最优臂的速度慢于softamx算法，平均回报率也低于它。

最后是总回报率：

总回报率的结果已经可以由上一张平均回报率看出来了。softmax最高，UCB第二，小量贪婪最低。

总结：

在实现UCB算法的过程中，首先捡回来了阅读英文文献的能力，UCB算法的内容基本是通过一本英文教材还有英文的维基百科上学习到的。其实以前英文一直挺好的，只是太久不用，忘了挺多。第二点就是对于C++STL库以及模板类的复习，平时stl库还能偶尔用一用，但是map,set等就用的特别少了，更别说模板类了，这次好好的复习了一遍。第三就是学习了一些新的东西，比如Json格式保存数据对，ssh登陆等等一些开发的额外知识。实习的收获确实很大。