Tarjan算法--有向图强连通分量算法
参考链接:https://www.byvoid.com/blog/scc-tarjan/
我的算法库:https://github.com/linyiqun/lyq-algorithms-lib
算法介绍
正如标题所介绍的那样,Tarjan算法的目标就是找出图中的连通图的,其实前提条件是这样的,在一个有向图中,有时必然会出现节点成环的情况,而在图内部的这些形成环的节点所构成的图就是我们所要找的,这个在实际生活中非常的有用,可以帮助我们解决最短距离之类的问题。
算法原理
概念
在介绍算法原理的之前,必须先明白一些概念:
1、强连通。在有向图G中,如果2个点之间存在至少一条路径,我们称这2个点为强连通。
2、强连通图。在图G中,如果其中任意的2个点都是强连通,则称图G为强连通图。
3、强连通分量。并不是所有的图中的任意2点之间都存在路径的,有些是部分节点连通,我们称这样的图为非强连通图,其中的部分强连通子图,就称为强连通分量。
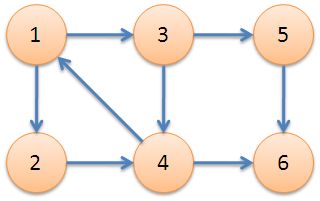
强连通分量就是本次算法要找的东西。下面给出一个图示:
在上面这个图中,{1, 2, 3, 4}是强连通分量,因为5,6是达不到的对于1, 2, 3, 4,来说,这里也将5,6单独作为强连通分量,可以理解为自己到自己是可达的(这样解释感觉比较勉强,但是定义也是允许这样的情况的)。
算法的过程
算法为每个节点定义了2个变量DFN[i]和LOW[i],DFN[i]代表的意思是i节点的搜索次序号,LOW[i]代表的是i节点或i的子节点能够追溯到的最早的节点的次序号,如果这么说没有理解的话,没有关系,可以看下面的伪代码:
tarjan(u)
{
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果节点v还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
repeat
v = S.pop // 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}算法的实现
算法的实现采用的例子还是上面这个例子,输入数据graphData.txt:
1 2 1 3 2 4 3 4 3 5 4 1 4 6 5 6
输入格式为标号1 标号2,代表的意思是存在标号1指向标号2节点的边。
有向图类Graph.java:
package Tarjan;
import java.util.ArrayList;
/**
* 有向图类
*
* @author lyq
*
*/
public class Graph {
// 图包含的点的标号
ArrayList<Integer> vertices;
// 图包含的有向边的分布,edges[i][j]中,i,j代表的是图的标号
int[][] edges;
// 图数据
ArrayList<String[]> graphDatas;
public Graph(ArrayList<String[]> graphDatas) {
this.graphDatas = graphDatas;
vertices = new ArrayList<>();
}
/**
* 利用图数据构造有向图
*/
public void constructGraph() {
int v1 = 0;
int v2 = 0;
int verticNum = 0;
for (String[] array : graphDatas) {
v1 = Integer.parseInt(array[0]);
v2 = Integer.parseInt(array[1]);
if (!vertices.contains(v1)) {
vertices.add(v1);
}
if (!vertices.contains(v2)) {
vertices.add(v2);
}
}
verticNum = vertices.size();
// 多申请1个空间,是标号和下标一致
edges = new int[verticNum + 1][verticNum + 1];
// 做边的初始化操作,-1 代表的是此方向没有连通的边
for (int i = 1; i < verticNum + 1; i++) {
for (int j = 1; j < verticNum + 1; j++) {
edges[i][j] = -1;
}
}
for (String[] array : graphDatas) {
v1 = Integer.parseInt(array[0]);
v2 = Integer.parseInt(array[1]);
edges[v1][v2] = 1;
}
}
}
算法工具类TarjanTool.java:
package Tarjan;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Stack;
/**
* Tarjan算法-有向图强连通分量算法
*
* @author lyq
*
*/
public class TarjanTool {
// 当前节点的遍历号
public static int currentSeq = 1;
// 图构造数据文件地址
private String graphFile;
// 节点u搜索的次序编号
private int DFN[];
// u或u的子树能回溯到的最早的节点的次序编号
private int LOW[];
// 由图数据构造的有向图
private Graph graph;
// 图遍历节点栈
private Stack<Integer> verticStack;
// 强连通分量结果
private ArrayList<ArrayList<Integer>> resultGraph;
// 图的未遍历的点的标号列表
private ArrayList<Integer> remainVertices;
// 图未遍历的边的列表
private ArrayList<int[]> remainEdges;
public TarjanTool(String graphFile) {
this.graphFile = graphFile;
readDataFile();
}
/**
* 从文件中读取数据
*
*/
private void readDataFile() {
File file = new File(graphFile);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
// 根据数据构造有向图
graph = new Graph(dataArray);
graph.constructGraph();
}
/**
* 初始化2个标量数组
*/
private void initDfnAndLow(){
int verticNum = 0;
verticStack = new Stack<>();
remainVertices = (ArrayList<Integer>) graph.vertices.clone();
remainEdges = new ArrayList<>();
resultGraph = new ArrayList<>();
for (int i = 0; i < graph.edges.length; i++) {
remainEdges.add(graph.edges[i]);
}
verticNum = graph.vertices.size();
DFN = new int[verticNum + 1];
LOW = new int[verticNum + 1];
// 初始化数组操作
for (int i = 1; i <= verticNum; i++) {
DFN[i] = Integer.MAX_VALUE;
LOW[i] = -1;
}
}
/**
* 搜索强连通分量
*/
public void searchStrongConnectedGraph() {
int label = 0;
int verticNum = graph.vertices.size();
initDfnAndLow();
// 设置第一个的DFN[1]=1;
DFN[1] = 1;
// 移除首个节点
label = remainVertices.get(0);
verticStack.add(label);
remainVertices.remove((Integer) 1);
while (remainVertices.size() > 0) {
for (int i = 1; i <= verticNum; i++) {
if (graph.edges[label][i] == 1) {
// 把与此边相连的节点也加入栈中
verticStack.add(i);
remainVertices.remove((Integer) i);
dfsSearch(verticStack);
}
}
LOW[label] = searchEarliestDFN(label);
// 重新回溯到第一个点进行DFN和LOW值的判断
if (LOW[label] == DFN[label]) {
popStackGraph(label);
}
}
printSCG();
}
/**
* 深度优先遍历的方式寻找强连通分量
*
* @param stack
* 存放的节点的当前栈
* @param seqNum
* 当前遍历的次序号
*/
private void dfsSearch(Stack<Integer> stack) {
int currentLabel = stack.peek();
// 设置搜索次序号,在原先的基础上增加1
currentSeq++;
DFN[currentLabel] = currentSeq;
LOW[currentLabel] = searchEarliestDFN(currentLabel);
int[] edgeVertic;
edgeVertic = remainEdges.get(currentLabel);
for (int i = 1; i < edgeVertic.length; i++) {
if (edgeVertic[i] == 1) {
// 如果剩余可选节点中包含此节点吗,则此节点添加
if (remainVertices.contains(i)) {
stack.add(i);
} else {
// 不包含,则跳过
continue;
}
// 将与此边相连的点加入栈中
remainVertices.remove((Integer) i);
remainEdges.set(currentLabel, null);
// 继续深度优先遍历
dfsSearch(stack);
}
}
if (LOW[currentLabel] == DFN[currentLabel]) {
popStackGraph(currentLabel);
}
}
/**
* 从栈中弹出局部结果
*
* @param label
* 弹出的临界标号
*/
private void popStackGraph(int label) {
// 如果2个值相等,则将此节点以及此节点后的点移出栈中
int value = 0;
ArrayList<Integer> scg = new ArrayList<>();
while (label != verticStack.peek()) {
value = verticStack.pop();
scg.add(0, value);
}
scg.add(0, verticStack.pop());
resultGraph.add(scg);
}
/**
* 当前的节点可能搜索到的最早的次序号
*
* @param label
* 当前的节点标号
* @return
*/
private int searchEarliestDFN(int label) {
// 判断此节点是否有子边
boolean hasSubEdge = false;
int minDFN = DFN[label];
// 如果搜索到的次序号已经是最小的次序号,则返回
if (DFN[label] == 1) {
return DFN[label];
}
int tempDFN = 0;
for (int i = 1; i <= graph.vertices.size(); i++) {
if (graph.edges[label][i] == 1) {
hasSubEdge = true;
// 如果在堆栈中和剩余节点中都未包含此节点说明已经被退栈了,不允许再次遍历
if (!remainVertices.contains(i) && !verticStack.contains(i)) {
continue;
}
tempDFN = searchEarliestDFN(i);
if (tempDFN < minDFN) {
minDFN = tempDFN;
}
}
}
// 如果没有子边,则搜索到的次序号就是它自身
if (!hasSubEdge && DFN[label] != -1) {
minDFN = DFN[label];
}
return minDFN;
}
/**
* 标准搜索强连通分量算法
*/
public void standardSearchSCG(){
initDfnAndLow();
verticStack.add(1);
remainVertices.remove((Integer)1);
//从标号为1的第一个节点开始搜索
dfsSearchSCG(1);
//输出结果中的强连通分量
printSCG();
}
/**
* 深度优先搜索强连通分量
*
* @param u
* 当前搜索的节点标号
*/
private void dfsSearchSCG(int u) {
DFN[u] = currentSeq;
LOW[u] = currentSeq;
currentSeq++;
for (int i = 1; i <graph.edges[u].length; i++) {
// 判断u,i两节点是否相连
if (graph.edges[u][i] == 1) {
// 相连的情况下,当i未被访问过的时候,加入栈中
if (remainVertices.contains(i)) {
verticStack.add(i);
remainVertices.remove((Integer) i);
// 递归搜索
dfsSearchSCG(i);
LOW[u] = (LOW[u] < LOW[i] ? LOW[u] : LOW[i]);
} else if(verticStack.contains(i)){
// 如果已经访问过,并且还未出栈过的
LOW[u] = (LOW[u] < DFN[i] ? LOW[u] : DFN[i]);
//LOW[u] = (LOW[u] < LOW[i] ? LOW[u] : LOW[i]); 如果都用LOW做判断,也可以通过测试
}
}
}
// 最后判断DFN和LOW是否相等
if (DFN[u] == LOW[u]) {
popStackGraph(u);
}
}
/**
* 输出有向图中的强连通分量
*/
private void printSCG() {
int i = 1;
String resultStr = "";
System.out.println("所有强连通分量子图:");
for (ArrayList<Integer> graph : resultGraph) {
resultStr = "";
resultStr += "强连通分量" + i + ":{";
for (Integer v : graph) {
resultStr += (v + ", ");
}
resultStr = (String) resultStr.subSequence(0,
resultStr.length() - 2);
resultStr += "}";
System.out.println(resultStr);
i++;
}
}
}
测试类Client.java:
package Tarjan;
/**
* Tarjan算法--有向图强连通分量算法
* @author lyq
*
*/
public class Client {
public static void main(String[] args){
//图构造数据文件地址
String graphFilePath = "C:\\Users\\lyq\\Desktop\\icon\\graphData.txt";
TarjanTool tool = new TarjanTool(graphFilePath);
//下面这个方法为改造的一点方法,还有点问题
//tool.searchStrongConnectedGraph();
tool.standardSearchSCG();
}
}
算法的执行步骤如图所示(手机拍摄的截图效果不佳,请不要见怪):
主要展示了随着遍历的顺序DFN和LOW数组的赋值情况,以及栈的内容变化情况
算法的输出结果:
所有强连通分量子图:
强连通分量1:{6}
强连通分量2:{5}
强连通分量3:{1, 2, 4, 3}
算法的遗漏点
在这个算法中,我写了2个算法,searchStrongConnectGraph是我自己在没有看伪代码写的,后来发现,意思有点曲解了,遇到循环图的时候也会有问题,后来马上看了伪代码,马上代码精简了很多,的确是非常强大的算法,第二点是我觉得在下面这个步骤中,判断是否可以合并在一起,因为我发现结果是一致的,都可以用LOW数组的值来判断。
// 相连的情况下,当i未被访问过的时候,加入栈中
if (remainVertices.contains(i)) {
verticStack.add(i);
remainVertices.remove((Integer) i);
// 递归搜索
dfsSearchSCG(i);
LOW[u] = (LOW[u] < LOW[i] ? LOW[u] : LOW[i]);
} else if(verticStack.contains(i)){
// 如果已经访问过,并且还未出栈过的
LOW[u] = (LOW[u] < DFN[i] ? LOW[u] : DFN[i]);
//LOW[u] = (LOW[u] < LOW[i] ? LOW[u] : LOW[i]); 如果都用LOW做判断,也可以通过测试
}
可能是为了让图中的边只允许被遍历一次的原因吧。
算法的突破点
很明显算法的突破口在于比较LOW和DFN的值,因为DFN的值在遍历顺序的就已经确定,所以问题的关键在于LOW值的确定,因为题目的要求是找到最早的那个搜索号,在这里会采用深度优先的方式一层层的寻找,如果找到的小的,就进行替换,如果最后找到的还是他自己的时候,说明这中间其实是一个环。然后把栈中当前节点的上方把节点全部移出。