Nearest Neighbor Image Scaling
Scaling of image is one frequently used task in any decent image processing software. Even if you say you don't, the software does. Ever zoomed your image for a closer look? Or used that convenient thumbnail preview? It all happens there, regardless of what you may be thinking.
Nearest neighbor is the simplest and fastest implementation of image scaling technique. It is very useful when speed is the main concern, for example when zooming image for editing or for a thumbnail preview. More complex variation of scaling algorithms are bilinear, bicubic, spline, sinc, and many others. Unlike simple nearest neighbor, this other variation uses interpolation of neighboring pixels, resulting in smoother image. Commercial implementation may have something called adaptive algorithm, where it has the capability of applying different level of interpolation on different area on an image - but this is beyond the scope of this article.
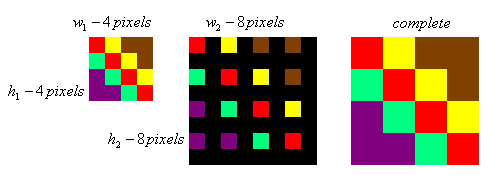
The principle in image scaling is to have a reference image and using this image as the base to construct a new scaled image. The constructed image will be smaller, larger, or equal in size depending on the scaling ratio. When enlarging an image, we are actually introducing empty spaces in the original base picture. From the image below, an image with dimension (w1 = 4, h1 = 4) is to be enlarged to (w2 = 8, h2 = 8). The black pixels represent empty spaces where interpolation is needed, and the complete picture is the result of nearest neighbor interpolation.
Scaling algorithm is to find appropiate spot to put the empty spaces inside the original image, and to fill all those spaces with livelier colors. For the nearest neighbor technique, the empty spaces will be replaced with the nearest neighboring pixel, hence the name. This results in a sharp but jaggy image, and if the enlarge scale is two, it would seems each pixel has doubled in size. Shrinking, in the other hand involves reduction of pixels and it means lost of irrecoverable information. In this case scaling algorithm is to find the right pixels to throw away.
Good scaling algorithm is one that can do up and down scalling without introducing too many conditions (theifs) in its implementation code, even better if there is none. Nearest neighbor is ano if, up down scaling algorithm. What information it needs are both the horizontal and vertical ratios between the original image and the (to be) scaled image. Consider again the diagram above, w1 and h1 are the width and height of an image, whereas w2 and h2 are the width and height when enlarged (or shrinked). Calculating the ratio for both horizontal and vertical plane is given by,
Of course the not equal to zero is a condition, and will eventually be translated as ifs in coding implementation. However, to be fair no algorithm is needed if one intend to shrink image to zero size, who the hell wants to do that?
Once ratio has been calculated prepare a buffer, or array, or whatever that can store information for the to be constructed image. The size should be enough to store w2*h2 of pixels. Check on the java code snippet below to find the implementation's simplicity for nearest neighbor algorithm.
public int[] resizePixels(int[] pixels,int w1,int h1,int w2,int h2) {
int[] temp = new int[w2*h2] ;
double x_ratio = w1/(double)w2 ;
double y_ratio = h1/(double)h2 ;
double px, py ;
for (int i=0;i<h2;i++) {
for (int j=0;j<w2;j++) {
px = Math.floor(j*x_ratio) ;
py = Math.floor(i*y_ratio) ;
temp[(i*w2)+j] = pixels[(int)((py*w1)+px)] ;
}
}
return temp ;
}
While this will work just fine, most of us are anxious with the slightest presence of floating point variables. Above function can be improved to deal with integer only variables without noticeable lost of precision - pixel wise :D
public int[] resizePixels(int[] pixels,int w1,int h1,int w2,int h2) {
int[] temp = new int[w2*h2] ;
// EDIT: added +1 to account for an early rounding problem
int x_ratio = (int)((w1<<16)/w2) +1;
int y_ratio = (int)((h1<<16)/h2) +1;
//int x_ratio = (int)((w1<<16)/w2) ;
//int y_ratio = (int)((h1<<16)/h2) ;
int x2, y2 ;
for (int i=0;i<h2;i++) {
for (int j=0;j<w2;j++) {
x2 = ((j*x_ratio)>>16) ;
y2 = ((i*y_ratio)>>16) ;
temp[(i*w2)+j] = pixels[(y2*w1)+x2] ;
}
}
return temp ;
}
What happen in this modification is we replace all floating point variables with integers and multiply the original size with 65536 before calculating ratios. The << operator is the bitwise shift left operator, and x<<16 is equivalent to x * 65536. The >>16 is equivalent to divide by 65536. It is also possible to replace most of the multiplication with just addition, can you see it? Once you get the above working, try yourself with addition only optimization. I'm sure it will be worth the effort.edit note: the original has problems up-sizing to 300%, 500%, 700%, and so on if you look real closely into the resulting image (thanks to Madhu for the observation). Taking an example of 300% sizing factor, the problem lies in calculating something akin to (1/3)*3. With Microsoft's calculator it gives back the answer 1, but trying to code that with integer only operation, 0 is the result. We can get around this by cheating with the math a bit by adding a small error factor for the ratio.
This implementation is sufficient for simple up and down scaling, except for condition zero size, but that should be an easy fix for someone like you. I have prepared some images scaled by the algorithm describe above. Don't mind the black stripes, they are just to show where the empty spaces are located when enlarging the original image.
Original image:
Scale 200%
Scale 200% with empty spaces shown (black pixels)
Scale 130%
Scale 130% with empty spaces shown (black pixels)
关于Image Engineering & Computer Vision的更多讨论与交流,敬请关注本博和新浪微博songzi_tea.