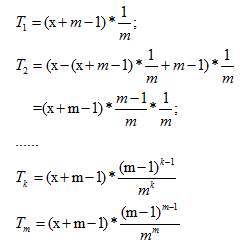猴子分桃问题的解决方法
猴子分桃问题的解决方法
1 问题
1979年，李政道博士给中国科技大学少年班出过一道智趣题：5只猴子分一堆桃子，怎么也分不成5等分，只好先去睡觉，准备第二天分。夜里1只猴子偷偷爬起来，先吃掉一个桃子，然后将其分为5等份，藏起自己的一份就去睡觉了；第二只猴子又爬起来，吃掉一个桃子后，也将桃子分成5等份，藏起自己的一份睡觉去了；以后的3只猴子都先后照此办理。问最初至少有多少个桃子？
现在考虑更加的一般性，说是m只猴子，问最初最少有多少个桃子？
2 解答：
2.1 递推解法
设最初有x个桃子，猴子的个数是定值m，用Tk表示第k的猴子占有的桃子总数，那么容易知道：
从上面的公式可以看出 必须是 的整数倍，所以可以推出：
2.2 整体思考法
这个算法算是吊炸天的，它也是最直接的，其实它也是在上面的推导过程中提炼出来的。
m只猴子，x个桃子，再借给猴子们(m-1)只桃子，这个时候第一只猴子得到的桃子是(x + m-1)的 1/m ，需要注意的是第一只猴子得到的桃子中并不包含借的桃子数目，也就是说借的(m-1)只桃子一个都没有给第一只猴子。然后第二只猴子分桃的时候，我们再把这没用上的(m-1)个桃子给补上，此时第二只猴子得到的桃子数目是第一次分完后剩下的 。也就是说第二只猴子分得：
，其中
是第一只猴子拿走桃子后再加上m-1个桃子的数目。以此类推，下一个猴子的拿的桃子数目都是前一个猴子拿的桃子数目的
，这样就很容易得出:
2.3 编程递归解决
如要递归只需要知道前后两次剩余桃子之间递推关系就可以了，这里很容易知道前后的关系是：
然后从x=1，开始遍历，直到x能满足每次都可以平均分配为止。代码如下所示：
#include <iostream>
using namespace std;
bool left(int x,int ntimes,int nMonkeys);
void main()
{
cout<<"Please input the monkeys"<<endl;
int nMonkeys;
cin>>nMonkeys;
int x = 2;
while( !left(x,nMonkeys,nMonkeys))
x++;
cout<<"The number of peach is :"<<x<<endl;
}
bool left(int x,int ntimes,int nMonkeys)
{
if (ntimes ==0)
return true;
else
{
if( (x-1)%nMonkeys !=0 )
return false;
else
return left( (x-1)*(nMonkeys-1)/nMonkeys,ntimes-1,nMonkeys);
}
}