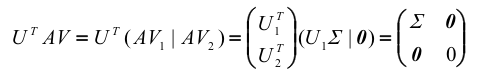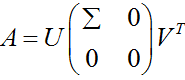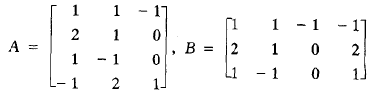机器学习之旅---奇异值分解
本次的讲解主要内容如下:
1.什么是奇异值分解?为什么任意实矩阵都存在奇异值分解?
2.怎么用C语言代码实现SVD分解?
3.实际应用:
基于SVD的图像压缩
基于SVD的协同过滤推荐系统
一、SVD奇异值分解概念
在多数情况下,数据中的一小段携带了数据集中的大部分信息,其他信息要么是噪声,要么就是毫不相干的信息。在线性代数中有很多矩阵分解技术,通过它们可以将原始矩阵表示成新的易于处理的形式。不同的矩阵分解技术具有不同的性质,有各自特定的应用场景。
奇异值分解SVD作为矩阵分解的一种类型,可以使我们只用很小的数据集就能表达原始数据集,它可以从噪声数据中抽取特征值。SVD可以将任意维数的原始数据集矩阵Data分解成三个矩阵U、Σ、VT,如下公式所示:
上述分解中会构建出一个矩阵Σ,该矩阵只有对角元素,其他元素均为0.此外,Σ的对角元素是从大到小排列的,这些对角线元素称为原始数据集矩阵Data的“奇异值”singular value。它与PCA特征的联系:PCA得到的是矩阵的特征值,奇异值就是矩阵Data*DataT特征值的平方根。
设A∈Rrm*n,ATA的特征值为:
当A为零矩阵时,它的所有奇异值均为零。一般的,矩阵A的奇异值个数等于A的列数,A的非零奇异值的个数等于A的秩。
接下来,首先用数学推导介绍SVD存在的必然性。
一些定义:
正交矩阵:
如果方正Q满足QTQ=QQT=I(或者等价的Q-1=QT),则称Q为正交矩阵。
非奇异矩阵:
若n阶矩阵A的行列式不为零,即 |A|≠0,则称A为非奇异矩阵或满秩矩阵,否则称A为奇异矩阵或降秩矩阵。
正定矩阵:
设M是n阶方阵,如果对任何非零向量z,都有 zTMz > 0,就称M正定矩阵。
定理证明:
定理1 (实对称矩阵正交相似于对角矩阵):
对任意n阶实对称矩阵A,都有n阶正交矩阵Q,使得

为了证明该定理,首先给出并证明两个引理:
- . 实对称矩阵特征值为实数
- 若任意n阶矩阵的特征值为实数,则有正交矩阵Q,使得
引理1,证明:
设λ为A的一个特征值,x为对应的特征向量,则有Ax = λx,因此
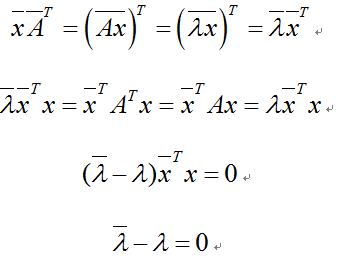
所以特征值必为实数。
引理2,利用数学归纳法证明:
当n=1时,结论显然成立
设对n-1阶矩阵的结论也成立,现在证明对n阶矩阵结论依然成立
令λ1为A的一个实特征值,相应的特征向量为a1,不妨设a1已单位化。把a1扩充为Rn的标准正交基a1, a2,…, an,构造矩阵X=(a2,…, an)和P=(a1,X),则P为正交矩阵且有:

于是,AP = (Aa1, AX)= (λ1a1, P(P-1AX)) = (λ1Pε1,P(P-1AX)) = P(λ1ε1, P-1AX)。设:

【个人理解:A->n*n,X->n*n-1,P->n*n,则P-1AX->n*n-1,正好这么拆,a’->1*n-1】
从而有:
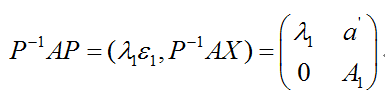
根据归纳假设,对于A1有n-1阶正交矩阵T,使得T-1A1T = TTA1T= At为上三角矩阵,现取:
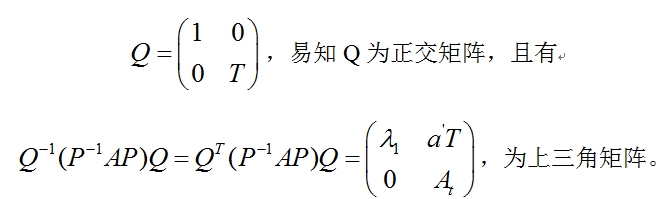
由于P和Q都是正交矩阵,而正交矩阵相乘结果R仍是正交矩阵,因此可以写作:
现在回到定理1的证明,因为A为实对称矩阵,则有引理1知,A的特征值均为实数。由引理2知,存在正交矩阵R,使得
C为上三角矩阵,而A=AT,则有C=CT,但C是上三角矩阵,CT为下三角矩阵,所以C必为对角矩阵。定理1得证。其中,C的对角线元素即为A的特征值构成。
定理2(奇异值分解):
设A∈R r m*n,则存在m阶正交矩阵U和n阶正交矩阵V,使得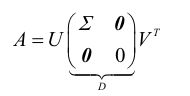
其中,Σ = diag(σ1,σ2,…, σr),即σ1, σ2,…,σr是A的非零奇异值,亦记作A=UDVT
证明:
记对称矩阵ATA的特征值为:
由对称矩阵的正交分解(定理1),我们有:
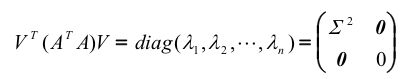
由第一个公式可以得到,
由第二个公式可以得到,
若记U=(u1, u2,…,um),V=(v1, v2,…,vn),根据SVD的分解,A可以表示为:
![]()
上式就是A的奇异值分解过程。
【我恨死CSDN的公式编辑了!!每次都贴图,烦的要命】
二、SVD奇异值分解求解及实现
上面的一堆推导,只是为了说明对任意矩阵都存在奇异值分解,而没有讲述如何求解奇异值分解。以下内容来自《徐士良C常用算法程序集(第二版)》,一般实矩阵的奇异值分解:
用household变换和变形QR算法对一般实矩阵进行奇异值分解,得到左右奇异向量U、V及奇异值矩阵D。
[个人认为具体怎么求SVD,大家不要去记和理解了,要用的时候能找到源码,方便其他移植即可]

例:求下面两个矩阵A和B的奇异值分解,ε取0.000001
C语言代码:
徐士良老头写的,可读性很差
bmuav.c:
#include "stdlib.h"
#include "math.h"
void ppp(double *a, double *e,double *s,double *v,int m,int n);
void sss(double *fg,double *cs);
/************************************************************************/
/* input:
/* a:存放m*n实矩阵A,返回时亦是奇异矩阵
/* m:行数 n:列数
/* u:存放m*m左奇异向量, v:存放n*n右奇异向量
/* eps:给定精度要求, ka: max(m,n)+1
/* output:
/* 返回值如果为负数,表示迭代了60次,还未求出奇异值;返回值为非负数,正常
/************************************************************************/
int bmuav(double *a,int m,int n,double *u,double *v,double eps,int ka)
{
int i,j,k,l,it,ll,kk,ix,iy,mm,nn,iz,m1,ks;
double d,dd,t,sm,sm1,em1,sk,ek,b,c,shh,fg[2],cs[2];
double *s,*e,*w;
s = (double *)malloc(ka*sizeof(double));
e = (double *)malloc(ka*sizeof(double));
w = (double *)malloc(ka*sizeof(double));
it=60;
k=n;
if (m-1<n)
k=m-1;
l=m;
if (n-2<m)
l=n-2;
if (l<0)
l=0;
ll=k;
if (l>k)
ll=l;
if (ll>=1)
{
for (kk=1; kk<=ll; kk++)
{
if (kk<=k)
{ d=0.0;
for (i=kk; i<=m; i++)
{
ix=(i-1)*n+kk-1; d=d+a[ix]*a[ix];
}
s[kk-1]=sqrt(d);
if (s[kk-1]!=0.0)
{
ix=(kk-1)*n+kk-1;
if (a[ix]!=0.0)
{
s[kk-1]=fabs(s[kk-1]);
if (a[ix]<0.0)
s[kk-1]=-s[kk-1];
}
for (i=kk; i<=m; i++)
{
iy=(i-1)*n+kk-1;
a[iy]=a[iy]/s[kk-1];
}
a[ix]=1.0+a[ix];
}
s[kk-1]=-s[kk-1];
}
if (n>=kk+1)
{
for (j=kk+1; j<=n; j++)
{
if ((kk<=k)&&(s[kk-1]!=0.0))
{
d=0.0;
for (i=kk; i<=m; i++)
{
ix=(i-1)*n+kk-1;
iy=(i-1)*n+j-1;
d=d+a[ix]*a[iy];
}
d=-d/a[(kk-1)*n+kk-1];
for (i=kk; i<=m; i++)
{
ix=(i-1)*n+j-1;
iy=(i-1)*n+kk-1;
a[ix]=a[ix]+d*a[iy];
}
}
e[j-1]=a[(kk-1)*n+j-1];
}
}
if (kk<=k)
{
for (i=kk; i<=m; i++)
{
ix=(i-1)*m+kk-1; iy=(i-1)*n+kk-1;
u[ix]=a[iy];
}
}
if (kk<=l)
{
d=0.0;
for (i=kk+1; i<=n; i++)
d=d+e[i-1]*e[i-1];
e[kk-1]=sqrt(d);
if (e[kk-1]!=0.0)
{
if (e[kk]!=0.0)
{
e[kk-1]=fabs(e[kk-1]);
if (e[kk]<0.0)
e[kk-1]=-e[kk-1];
}
for (i=kk+1; i<=n; i++)
e[i-1]=e[i-1]/e[kk-1];
e[kk]=1.0+e[kk];
}
e[kk-1]=-e[kk-1];
if ((kk+1<=m)&&(e[kk-1]!=0.0))
{
for (i=kk+1; i<=m; i++) w[i-1]=0.0;
for (j=kk+1; j<=n; j++)
for (i=kk+1; i<=m; i++)
w[i-1]=w[i-1]+e[j-1]*a[(i-1)*n+j-1];
for (j=kk+1; j<=n; j++)
for (i=kk+1; i<=m; i++)
{
ix=(i-1)*n+j-1;
a[ix]=a[ix]-w[i-1]*e[j-1]/e[kk];
}
}
for (i=kk+1; i<=n; i++)
v[(i-1)*n+kk-1]=e[i-1];
}
}
}
mm=n;
if (m+1<n)
mm=m+1;
if (k<n)
s[k]=a[k*n+k];
if (m<mm)
s[mm-1]=0.0;
if (l+1<mm)
e[l]=a[l*n+mm-1];
e[mm-1]=0.0;
nn=m;
if (m>n)
nn=n;
if (nn>=k+1)
{
for (j=k+1; j<=nn; j++)
{
for (i=1; i<=m; i++)
u[(i-1)*m+j-1]=0.0;
u[(j-1)*m+j-1]=1.0;
}
}
if (k>=1)
{
for (ll=1; ll<=k; ll++)
{
kk=k-ll+1; iz=(kk-1)*m+kk-1;
if (s[kk-1]!=0.0)
{
if (nn>=kk+1)
for (j=kk+1; j<=nn; j++)
{
d=0.0;
for (i=kk; i<=m; i++)
{
ix=(i-1)*m+kk-1;
iy=(i-1)*m+j-1;
d=d+u[ix]*u[iy]/u[iz];
}
d=-d;
for (i=kk; i<=m; i++)
{
ix=(i-1)*m+j-1;
iy=(i-1)*m+kk-1;
u[ix]=u[ix]+d*u[iy];
}
}
for (i=kk; i<=m; i++)
{
ix=(i-1)*m+kk-1;
u[ix]=-u[ix];
}
u[iz]=1.0+u[iz];
if (kk-1>=1)
for (i=1; i<=kk-1; i++)
u[(i-1)*m+kk-1]=0.0;
}
else
{
for (i=1; i<=m; i++)
u[(i-1)*m+kk-1]=0.0;
u[(kk-1)*m+kk-1]=1.0;
}
}
}
for (ll=1; ll<=n; ll++)
{
kk=n-ll+1; iz=kk*n+kk-1;
if ((kk<=l)&&(e[kk-1]!=0.0))
{
for (j=kk+1; j<=n; j++)
{
d=0.0;
for (i=kk+1; i<=n; i++)
{
ix=(i-1)*n+kk-1; iy=(i-1)*n+j-1;
d=d+v[ix]*v[iy]/v[iz];
}
d=-d;
for (i=kk+1; i<=n; i++)
{
ix=(i-1)*n+j-1;
iy=(i-1)*n+kk-1;
v[ix]=v[ix]+d*v[iy];
}
}
}
for (i=1; i<=n; i++)
v[(i-1)*n+kk-1]=0.0;
v[iz-n]=1.0;
}
for (i=1; i<=m; i++)
for (j=1; j<=n; j++)
a[(i-1)*n+j-1]=0.0;
m1=mm;
it=60;
while (1==1)
{
if (mm==0)
{
ppp(a,e,s,v,m,n);
free(s); free(e); free(w);
return(1);
}
if (it==0)
{
ppp(a,e,s,v,m,n);
free(s); free(e); free(w);
return(-1);
}
kk=mm-1;
while ((kk!=0)&&(fabs(e[kk-1])!=0.0))
{
d=fabs(s[kk-1])+fabs(s[kk]);
dd=fabs(e[kk-1]);
if (dd>eps*d)
kk=kk-1;
else
e[kk-1]=0.0;
}
if (kk==mm-1)
{
kk=kk+1;
if (s[kk-1]<0.0)
{
s[kk-1]=-s[kk-1];
for (i=1; i<=n; i++)
{
ix=(i-1)*n+kk-1; v[ix]=-v[ix];
}
}
while ((kk!=m1)&&(s[kk-1]<s[kk]))
{
d=s[kk-1]; s[kk-1]=s[kk]; s[kk]=d;
if (kk<n)
for (i=1; i<=n; i++)
{
ix=(i-1)*n+kk-1; iy=(i-1)*n+kk;
d=v[ix]; v[ix]=v[iy]; v[iy]=d;
}
if (kk<m)
for (i=1; i<=m; i++)
{
ix=(i-1)*m+kk-1; iy=(i-1)*m+kk;
d=u[ix]; u[ix]=u[iy]; u[iy]=d;
}
kk=kk+1;
}
it=60;
mm=mm-1;
}
else
{
ks=mm;
while ((ks>kk)&&(fabs(s[ks-1])!=0.0))
{
d=0.0;
if (ks!=mm)
d=d+fabs(e[ks-1]);
if (ks!=kk+1)
d=d+fabs(e[ks-2]);
dd=fabs(s[ks-1]);
if (dd>eps*d)
ks=ks-1;
else
s[ks-1]=0.0;
}
if (ks==kk)
{
kk=kk+1;
d=fabs(s[mm-1]);
t=fabs(s[mm-2]);
if (t>d)
d=t;
t=fabs(e[mm-2]);
if (t>d)
d=t;
t=fabs(s[kk-1]);
if (t>d)
d=t;
t=fabs(e[kk-1]);
if (t>d)
d=t;
sm=s[mm-1]/d;
sm1=s[mm-2]/d;
em1=e[mm-2]/d;
sk=s[kk-1]/d;
ek=e[kk-1]/d;
b=((sm1+sm)*(sm1-sm)+em1*em1)/2.0;
c=sm*em1; c=c*c; shh=0.0;
if ((b!=0.0)||(c!=0.0))
{
shh=sqrt(b*b+c);
if (b<0.0)
shh=-shh;
shh=c/(b+shh);
}
fg[0]=(sk+sm)*(sk-sm)-shh;
fg[1]=sk*ek;
for (i=kk; i<=mm-1; i++)
{
sss(fg,cs);
if (i!=kk)
e[i-2]=fg[0];
fg[0]=cs[0]*s[i-1]+cs[1]*e[i-1];
e[i-1]=cs[0]*e[i-1]-cs[1]*s[i-1];
fg[1]=cs[1]*s[i];
s[i]=cs[0]*s[i];
if ((cs[0]!=1.0)||(cs[1]!=0.0))
for (j=1; j<=n; j++)
{
ix=(j-1)*n+i-1;
iy=(j-1)*n+i;
d=cs[0]*v[ix]+cs[1]*v[iy];
v[iy]=-cs[1]*v[ix]+cs[0]*v[iy];
v[ix]=d;
}
sss(fg,cs);
s[i-1]=fg[0];
fg[0]=cs[0]*e[i-1]+cs[1]*s[i];
s[i]=-cs[1]*e[i-1]+cs[0]*s[i];
fg[1]=cs[1]*e[i];
e[i]=cs[0]*e[i];
if (i<m)
if ((cs[0]!=1.0)||(cs[1]!=0.0))
for (j=1; j<=m; j++)
{
ix=(j-1)*m+i-1;
iy=(j-1)*m+i;
d=cs[0]*u[ix]+cs[1]*u[iy];
u[iy]=-cs[1]*u[ix]+cs[0]*u[iy];
u[ix]=d;
}
}
e[mm-2]=fg[0];
it=it-1;
}
else
{
if (ks==mm)
{
kk=kk+1;
fg[1]=e[mm-2]; e[mm-2]=0.0;
for (ll=kk; ll<=mm-1; ll++)
{
i=mm+kk-ll-1;
fg[0]=s[i-1];
sss(fg,cs);
s[i-1]=fg[0];
if (i!=kk)
{
fg[1]=-cs[1]*e[i-2];
e[i-2]=cs[0]*e[i-2];
}
if ((cs[0]!=1.0)||(cs[1]!=0.0))
for (j=1; j<=n; j++)
{
ix=(j-1)*n+i-1;
iy=(j-1)*n+mm-1;
d=cs[0]*v[ix]+cs[1]*v[iy];
v[iy]=-cs[1]*v[ix]+cs[0]*v[iy];
v[ix]=d;
}
}
}
else
{
kk=ks+1;
fg[1]=e[kk-2];
e[kk-2]=0.0;
for (i=kk; i<=mm; i++)
{
fg[0]=s[i-1];
sss(fg,cs);
s[i-1]=fg[0];
fg[1]=-cs[1]*e[i-1];
e[i-1]=cs[0]*e[i-1];
if ((cs[0]!=1.0)||(cs[1]!=0.0))
for (j=1; j<=m; j++)
{
ix=(j-1)*m+i-1;
iy=(j-1)*m+kk-2;
d=cs[0]*u[ix]+cs[1]*u[iy];
u[iy]=-cs[1]*u[ix]+cs[0]*u[iy];
u[ix]=d;
}
}
}
}
}
}
return(1);
}
static void ppp(double a[], double e[],double s[],double v[],int m,int n)
{
int i,j,p,q;
double d;
if (m>=n) i=n;
else i=m;
for (j=1; j<=i-1; j++)
{
a[(j-1)*n+j-1]=s[j-1];
a[(j-1)*n+j]=e[j-1];
}
a[(i-1)*n+i-1]=s[i-1];
if (m<n)
a[(i-1)*n+i]=e[i-1];
for (i=1; i<=n-1; i++)
for (j=i+1; j<=n; j++)
{
p=(i-1)*n+j-1; q=(j-1)*n+i-1;
d=v[p]; v[p]=v[q]; v[q]=d;
}
return;
}
static void sss(double fg[],double cs[])
{
double r,d;
if ((fabs(fg[0])+fabs(fg[1]))==0.0)
{
cs[0]=1.0; cs[1]=0.0; d=0.0;
}
else
{
d=sqrt(fg[0]*fg[0]+fg[1]*fg[1]);
if (fabs(fg[0])>fabs(fg[1]))
{
d=fabs(d);
if (fg[0]<0.0) d=-d;
}
if (fabs(fg[1])>=fabs(fg[0]))
{
d=fabs(d);
if (fg[1]<0.0) d=-d;
}
cs[0]=fg[0]/d; cs[1]=fg[1]/d;
}
r=1.0;
if (fabs(fg[0])>fabs(fg[1]))
r=cs[1];
else
if (cs[0]!=0.0) r=1.0/cs[0];
fg[0]=d;
fg[1]=r;
return;
}
brmul.c:矩阵乘法
void brmul(double *a,double *b,int m,int n,int k,double *c)
{
int i,j,l,u;
for (i=0; i<=m-1; i++)
for (j=0; j<=k-1; j++)
{
u=i*k+j; c[u]=0.0;
for (l=0; l<=n-1; l++)
c[u]=c[u]+a[i*n+l]*b[l*k+j];
}
return;
}
调用:
// svd.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "bmuav.c"
#include "brmul.c"
extern void brmul(double *a,double *b,int m,int n,int k,double *c);
extern int bmuav(double *a,int m,int n,double *u,double *v,double eps,int ka);
int _tmain(int argc, _TCHAR* argv[])
{
int i,j;
static double a[4][3]={ {1.0,1.0,-1.0},{2.0,1.0,0.0},
{1.0,-1.0,0.0},{-1.0,2.0,1.0}};
static double b[3][4]={ {1.0,1.0,-1.0,-1.0},{2.0,1.0,
0.0,2.0},{1.0,-1.0,0.0,1.0}};
static double u[4][4],v[3][3],c[4][3],d[3][4];
double eps;
eps=0.000001;
i=bmuav(&a[0][0],4,3,&u[0][0],&v[0][0],eps,5);
printf("\n");
printf("EXAMPLE(1)\n");
printf("\n");
printf("i=%d\n",i);
printf("\n");
printf("MAT U IS:\n");
for (i=0; i<=3; i++)
{ for (j=0; j<=3; j++)
printf("%13.7e ",u[i][j]);
printf("\n");
}
printf("\n");
printf("MAT V IS:\n");
for (i=0; i<=2; i++)
{ for (j=0; j<=2; j++)
printf("%13.7e ",v[i][j]);
printf("\n");
}
printf("\n");
printf("MAT A IS:\n");
for (i=0; i<=3; i++)
{ for (j=0; j<=2; j++)
printf("%13.7e ",a[i][j]);
printf("\n");
}
printf("\n\n");
printf("MAT UAV IS:\n");
brmul(&u[0][0],&a[0][0],4,4,3,&c[0][0]);
brmul(&c[0][0],&v[0][0],4,3,3,&a[0][0]);
for (i=0; i<=3; i++)
{ for (j=0; j<=2; j++)
printf("%13.7e ",a[i][j]);
printf("\n");
}
printf("\n\n");
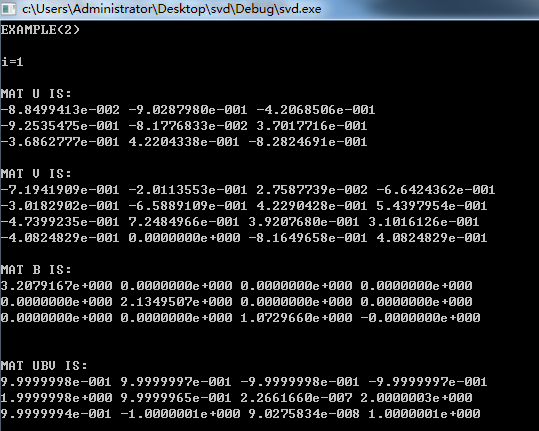
printf("EXAMPLE(2)\n");
printf("\n");
i=bmuav(&b[0][0],3,4,&v[0][0],&u[0][0],eps,5);
printf("i=%d\n",i);
printf("\n");
printf("MAT U IS:\n");
for (i=0; i<=2; i++)
{ for (j=0; j<=2; j++)
printf("%13.7e ",v[i][j]);
printf("\n");
}
printf("\n");
printf("MAT V IS:\n");
for (i=0; i<=3; i++)
{ for (j=0; j<=3; j++)
printf("%13.7e ",u[i][j]);
printf("\n");
}
printf("\n");
printf("MAT B IS:\n");
for (i=0; i<=2; i++)
{ for (j=0; j<=3; j++)
printf("%13.7e ",b[i][j]);
printf("\n");
}
printf("\n\n");
printf("MAT UBV IS:\n");
brmul(&v[0][0],&b[0][0],3,3,4,&d[0][0]);
brmul(&d[0][0],&u[0][0],3,4,4,&b[0][0]);
for (i=0; i<=2; i++)
{ for (j=0; j<=3; j++)
printf("%13.7e ",b[i][j]);
printf("\n");
}
printf("\n");
return 0;
}
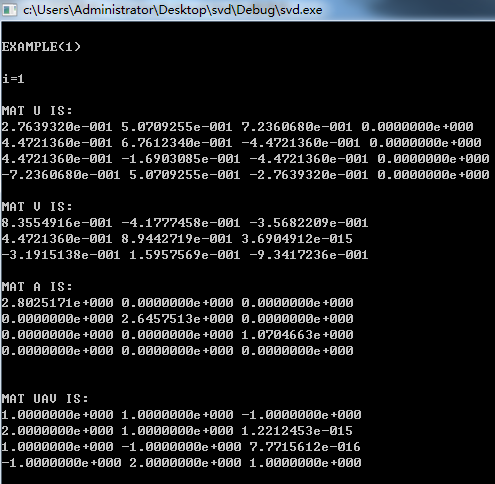
程序结果:
三、SVD应用实例
1. 基于SVD的图像压缩
这个例子比较简单,首先进行奇异值分解,得到奇异值矩阵,和左右奇异向量。然后由于只要很少的奇异值,就能包含绝大部分被分解的矩阵信息,因此我们挑选不同数量的奇异值,重构图像,比较差异。这边分别实现了灰度图、RGB三色图的SVD分解。【奇异值到底选多少,自己打印奇异值矩阵,从大到小排序的,小到什么程度就舍弃,实际情况实际操作。。。】#include "stdafx.h"
#include "cv.h"
#include "highgui.h"
#include "bmuav.c"
#include "brmul.c"
#define max(a,b) (((a) > (b)) ? (a) : (b))
extern void brmul(double *a,double *b,int m,int n,int k,double *c);
extern int bmuav(double *a,int m,int n,double *u,double *v,double eps,int ka);
int Process(IplImage *src);
int _tmain(int argc, _TCHAR* argv[])
{
IplImage *src = cvLoadImage("test1.jpg", CV_LOAD_IMAGE_GRAYSCALE);
Process(src);
return 0;
}
int Process(IplImage *src)
{
double *data, *u, *v, *c;
int height, width, i, j, ka;
double eps;
int scale;
IplImage *dst;
dst = cvCreateImage(cvSize(src->width,src->height),IPL_DEPTH_8U,1);
eps=0.000001;
height = src->height;
width = src->widthStep;
//allocate memory for matrix
data = (double *)malloc(sizeof(double)*height*width);
u = (double *)malloc(sizeof(double)*height*height);
v = (double *)malloc(sizeof(double)*width*width);
memset(u,0,sizeof(double)*height*height);
memset(v,0,sizeof(double)*width*width);
if(NULL == data || NULL == u || NULL == v)
{
return -1;
}
//assign value
for(i = 0;i < height;i++)
{
for(j = 0;j < width;j++)
{
data[i*width+j] = (double)(unsigned char)src->imageData[i*width+j];
}
}
ka = max(height,width) + 1;
bmuav(data, height, width, u, v, eps, ka);
//dump svd, scale is selected by watching top xxx large data
/*for (i=0; i<=100; i++)
{
for (j=0; j<=100; j++)
printf("%f", data[i*width+j]);
printf("\n");
}*/
//reconstruction
scale = 50;
for(i = scale;i<height;i++)
{
data[i*width+i] = 0;
}
/*c needs to be initilized here ,but in matrix mutiply funciton*/
c = (double *)malloc(sizeof(double)*height*width);
brmul(u, data ,height, height, width, c);
brmul(c, v, height, width, width, data);
//assign value
for(i = 0;i < height;i++)
{
for(j = 0;j < width;j++)
{
dst->imageData[i*width+j] = (unsigned char)data[i*width+j];
}
}
cvSaveImage("result.jpg",dst);
free(data);free(u);free(v);
cvReleaseImage(&dst);
return 0;
}
结果:
彩色图:
#include "stdafx.h"
#include "cv.h"
#include "highgui.h"
#include "bmuav.c"
#include "brmul.c"
#define max(a,b) (((a) > (b)) ? (a) : (b))
extern void brmul(double *a,double *b,int m,int n,int k,double *c);
extern int bmuav(double *a,int m,int n,double *u,double *v,double eps,int ka);
int Process(IplImage *src);
int _tmain(int argc, _TCHAR* argv[])
{
IplImage *src = cvLoadImage("test3.jpg", CV_LOAD_IMAGE_UNCHANGED);
Process(src);
return 0;
}
int Process(IplImage *src)
{
double *data_r, *u_r, *v_r, *c_r;
double *data_g, *u_g, *v_g, *c_g;
double *data_b, *u_b, *v_b, *c_b;
int height, width, i, j, ka;
double eps;
int scale;
IplImage *dst;
dst = cvCreateImage(cvSize(src->width,src->height),IPL_DEPTH_8U,3);
eps=0.000001;
height = src->height;
width = src->width;
//allocate memory for matrix
data_r = (double *)malloc(sizeof(double)*height*width);
u_r = (double *)malloc(sizeof(double)*height*height);
v_r = (double *)malloc(sizeof(double)*width*width);
data_g = (double *)malloc(sizeof(double)*height*width);
u_g = (double *)malloc(sizeof(double)*height*height);
v_g = (double *)malloc(sizeof(double)*width*width);
data_b = (double *)malloc(sizeof(double)*height*width);
u_b = (double *)malloc(sizeof(double)*height*height);
v_b = (double *)malloc(sizeof(double)*width*width);
memset(u_r,0,sizeof(double)*height*height);
memset(v_r,0,sizeof(double)*width*width);
memset(u_g,0,sizeof(double)*height*height);
memset(v_g,0,sizeof(double)*width*width);
memset(u_b,0,sizeof(double)*height*height);
memset(v_b,0,sizeof(double)*width*width);
//assign value
for(i = 0;i < height;i++)
{
for(j = 0;j < width;j++)
{
data_r[i*width+j] = (double)(unsigned char)src->imageData[i*src->widthStep+j*src->nChannels+2];
data_g[i*width+j] = (double)(unsigned char)src->imageData[i*src->widthStep+j*src->nChannels+1];
data_b[i*width+j] = (double)(unsigned char)src->imageData[i*src->widthStep+j*src->nChannels+0];
}
}
ka = max(height,width) + 1;
bmuav(data_r, height, width, u_r, v_r, eps, ka);
bmuav(data_g, height, width, u_g, v_g, eps, ka);
bmuav(data_b, height, width, u_b, v_b, eps, ka);
//dump svd, scale is selected by watching top xxx large data
/*for (i=0; i<=100; i++)
{
for (j=0; j<=100; j++)
printf("%f", data[i*width+j]);
printf("\n");
}*/
//reconstruction
scale = 50;
for(i = scale;i<height;i++)
{
data_r[i*width+i] = 0;
data_g[i*width+i] = 0;
data_b[i*width+i] = 0;
}
/*c needs to be initilized here ,but in matrix mutiply funciton*/
c_r = (double *)malloc(sizeof(double)*height*width);
c_g = (double *)malloc(sizeof(double)*height*width);
c_b = (double *)malloc(sizeof(double)*height*width);
brmul(u_r, data_r ,height, height, width, c_r);
brmul(c_r, v_r, height, width, width, data_r);
brmul(u_g, data_g ,height, height, width, c_g);
brmul(c_g, v_g, height, width, width, data_g);
brmul(u_b, data_b ,height, height, width, c_b);
brmul(c_b, v_b, height, width, width, data_b);
//assign value
for(i = 0;i < height;i++)
{
for(j = 0;j < width;j++)
{
dst->imageData[i*src->widthStep+j*src->nChannels + 0] = (unsigned char)data_b[i*width+j];
dst->imageData[i*src->widthStep+j*src->nChannels + 1] = (unsigned char)data_g[i*width+j];
dst->imageData[i*src->widthStep+j*src->nChannels + 2] = (unsigned char)data_r[i*width+j];
}
}
cvSaveImage("result.jpg",dst);
cvReleaseImage(&dst);
free(u_r);free(v_r);free(c_r);free(data_r);
free(u_g);free(v_g);free(c_g);free(data_g);
free(u_b);free(v_b);free(c_b);free(data_b);
return 0;
}
效果图:
注意:SVD压缩只是为了存储更少的数据来表达原始图像,在重构图像时,奇异值矩阵仍旧是要和原始图像大小一样的,只不过大部分地方用0填充罢了。
2 . 基于SVD的协同过滤推荐系统
这个例子比较有趣,推荐系统已存在很多年了。大家在网购时,商家总会根据大家的购买的历史记录给大家推荐新的商品及服务。实现方法有多种,这次只讲基于协同过滤的方法。所谓协同过滤,就是将用户和其他用户的数据进行对比来实现推荐的。前端输入的原始数据如下:【评分:0-5】

【后话:很严重的问题,就是当用户间没有交集,推荐系统就无法工作咯】
下面就构建一个餐饮网站的推荐系统。假设一个人在家决定外出吃饭,但是他并不知道该到哪去吃饭,该点什么菜。我们可以构建一个基本的推荐引擎,它能够帮助用户寻找没有尝过的菜肴,然后通过SVD来减少特征空间并提高反馈的速度。
a. 基本的推荐引擎
推荐系统的工作过程:给定一个用户,系统会为此用户返回N个最好的推荐,为了实现这一点我们需要做:
- 寻找用户没有评级的菜肴
- 在用户没有评级的物品中,对每个物品预计一个可能的评级分数。也就是说,我们的系统认为用户可能会对物品的打分
- 对这些物品的评分从高到低排序,返回前N个
之前说将用户和其他用户的数据进行对比来实现推荐,那么我们借助什么手段预测评分呢?有两种方案:
基于用户的相似度:行与行之间的比较
基于菜肴的相似度:列与列之间的比较
【距离公式可采用欧氏距离、余弦距离、皮尔逊距离等等】
那么到底使用哪一种相似度呢?这取决于菜肴和用户的数目。无论基于哪种相似度,它的计算时间都会随着用户/物品的数量的增加而增加。对于大部分产品导向的推荐引擎而言,用户的数量往往大于商品的数量。因此这里采用基于菜肴的相似度计算。
各种相似度计算代码:void matrix_reverse(double *src,double *dest,int row,int col)
{
int i,j;
for(i = 0;i < col;i++)
{
for(j = 0;j < row;j++)
{
dest[i * row + j] = src[j * col + i];
}
}
}
/*欧氏距离*/
double ecludSim(double *dataMat,int *overLap, int n, int count, int item, int j)
{
double total = 0.0;
int i=0, index=0;
for(i = 0;i < count;i++)
{
index = overLap[i];
total = total + (dataMat[index*n+item] - dataMat[index*n+j]) * (dataMat[index*n+item] - dataMat[index*n+j]);
}
total = sqrt(total);
return 1.0/(1.0 + total);
}
double ecludSim2(double *dataMat,int *overLap, int n, int scale, int item, int j)
{
double total = 0.0;
int i = 0;
for(i = 0;i < scale;i++)
{
total = total + (dataMat[item*n+i] - dataMat[j*n+i]) * (dataMat[item*n+i] - dataMat[j*n+i]);
}
total = sqrt(total);
return 1.0/(1.0 + total);
}
/*余弦距离*/
double cosSim(double *dataMat,int *overLap, int n, int count, int item, int j)
{
double totalA=0.0, totalB=0.0, totalM=0.0;
double result=0.0;
int i, index;
for(i = 0;i < count;i++)
{
index = overLap[i];
totalA = totalA + dataMat[index*n+item] * dataMat[index*n+item];
totalB = totalB + dataMat[index*n+j] * dataMat[index*n+j];
totalM = totalM + dataMat[index*n+item] * dataMat[index*n+j];
}
result = totalM / (sqrt(totalA) * sqrt(totalB));
return 0.5 + 0.5 * result;
}
double cosSim2(double *dataMat,int *overLap, int n, int scale, int item, int j)
{
double totalA=0.0, totalB=0.0, totalM=0.0;
double result=0.0;
int i;
for(i=0;i<scale;i++)
{
totalA = totalA + dataMat[item*n+i] * dataMat[item*n+i];
totalB = totalB + dataMat[j*n+i] * dataMat[j*n+i];
totalM = totalM + dataMat[item*n+i] * dataMat[j*n+i];
}
result = totalM / (sqrt(totalA) * sqrt(totalB));
return 0.5 + 0.5 * result;
}
【机器学习是用Python写的,操作矩阵很方便,这边C语言很笨重,所以没有做到代码重用,XXX2表示SVD推荐系统时用的距离函数,XXX是标准推荐系统】
预测评价的原理:假设要预测用户A的第k个未评价菜肴的评分,我们可以遍历整个数据矩阵寻找用户A和其他用户都评价过的其他菜肴j,计算用户A和其他用户针对菜肴j的评价的相似距离,若有多个这种共同的评价,则累加相似度。最后的计算公式:
第k个菜肴的评分 = sum(累加的相似度 * A对j的评分 ) / 累加相似度
下面先给出主函数吧,否则太乱了:
// recommand.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <math.h>
#include <stdlib.h>
#include <string.h>
#include "bmuav.c"
#include "brmul.c"
#define max(a,b) (((a) > (b)) ? (a) : (b))
typedef double (*func)(double *dataMat,int *overLap, int n, int count, int item, int j);
typedef double (*Est)(double *dataMat, int user, func simMeas, int item, int m, int n);
extern void brmul(double *a,double *b,int m,int n,int k,double *c);
extern int bmuav(double *a,int m,int n,double *u,double *v,double eps,int ka);
extern void matrix_reverse(double *src,double *dest,int row,int col);
double standEst(double *dataMat, int user, func simMeas, int item, int m, int n);
double svdEst(double *dataMat, int user, func simMeas, int item, int m, int n);
double cosSim(double *dataMat,int *overLap, int n, int count, int item, int j);
double cosSim2(int *dataMat,int *overLap, int n, int scale, int item, int j);
double ecludSim(double *dataMat,int *overLap, int n, int count, int item, int j);
double ecludSim2(double *dataMat,int *overLap, int n, int count, int item, int j);
double recommend(double *dataMat,int n, int m, int user, func simMeas=cosSim, Est estMethod=standEst);
int _tmain(int argc, _TCHAR* argv[])
{
int user;
double data[7][5] = {{4, 4, 0, 2, 2},
{4, 0, 0, 3, 3},
{4, 0, 0, 1, 1},
{1, 1, 1, 2, 0},
{2, 2, 2, 0, 0},
{5, 5, 5, 0, 0},
{1, 1, 1, 0, 0}};
double data_2[11][11] = {{2, 0, 0, 4, 4, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5},
{0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0},
{3, 3, 4, 0, 3, 0, 0, 2, 2, 0, 0},
{5, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0},
{4, 0, 4, 0, 0, 0, 0, 0, 0, 0, 5},
{0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 4},
{0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0},
{0, 0, 0, 3, 0, 0, 0, 0, 4, 5, 0},
{1, 1, 2, 1, 1, 2, 1, 0, 4, 5, 0}};
user = 2;
//recommend(&data[0][0], 5, 7, user, cosSim, standEst);
//recommend(&data[0][0], 5, 7, user, ecludSim, standEst);
//recommend(&data_2[0][0], 11, 11, user, ecludSim2, svdEst);
recommend(&data_2[0][0], 11, 11, user, cosSim2, svdEst);
return 0;
}
double recommend(double *dataMat,int n, int m, int user, func simMeas, Est estMethod)
{
int i,count, item,j;
int *record=0;
double *temp_vote=0;
double temp=0, temp2=0;
record = (int *)malloc(sizeof(int)*n);
memset(record, 0, sizeof(int)*n);
count = 0;
//寻找user用户未评价物品
for(i = 0;i < n;i++)
{
if(dataMat[user*n+i] == 0)
{
record[count++] = i;
}
}
if (count == 0)
{
printf("该用户评价了所有的物品\n");
return -1; //用户评价了所有的物品
}
temp_vote = (double *)malloc(sizeof(double)*count);
memset(temp_vote,0,sizeof(double)*count);
for(i=0;i<count;i++)
{
item = record[i];
temp_vote[i] = estMethod(dataMat, user, simMeas, item, m, n);
}
//排序
for(i=0;i<count;i++)
{
for(j=0;j<count - i;j++)
{
if(temp_vote[j]<temp_vote[j+1])
{
temp = temp_vote[j];
temp_vote[j] = temp_vote[j+1];
temp_vote[j+1] = temp;
temp2 = record[j];
record[j] = record[j+1];
record[j+1] = temp2;
}
}
}
//dump result
for(i = 0;i < count;i++)
{
printf("food label %d,value to recommand %f\n", record[i], temp_vote[i]);
}
free(record);
return 0;
}
标准推荐系统:
double standEst(double *dataMat, int user, func simMeas, int item, int m, int n)
{
double simTotal=0, ratSimTotal=0, userRating=0, similarity=0;
int j=0, k=0, count=0;
int *overLap=0; //记录交集
overLap = (int *)malloc(sizeof(int)*m);
for (j = 0;j < n;j++)
{
userRating = dataMat[user*n+j]; //user用户评价过的
if(userRating == 0)
continue;
count = 0;
memset(overLap, 0, sizeof(int)*m);
for(k = 0;k < m;k++)
{
if(dataMat[k*n+item] > 0 && dataMat[k*n+j] > 0) //寻找用户都评级的两个物品
{
overLap[count++] = k;
}
}
if (count == 0)
{
similarity = 0;
}else
{
similarity = simMeas(dataMat, overLap, n, count, item, j);
}
simTotal += similarity;
ratSimTotal += similarity * userRating;
}
free(overLap);
if(0 == simTotal)
{
return 0.0;
}else
{
return ratSimTotal/simTotal;
}
}对于data矩阵,用户2,对应第三行,预测结果:
b. 基于SVD的推荐引擎
在数据矩阵非常稀疏时,基于SVD的推荐引擎性能就会比标准的好很多。我们利用SVD将所有菜肴隐射到一个低维空间中,再利用和前面一样的相似度计算方法来进行推荐。
double svdEst(double *dataMat, int user, func simMeas, int item, int m, int n)
{
double *u, *v, *data_new, *I, *dataMat2, *dataMatCopy, *svdMat;
double simTotal=0, ratSimTotal=0, userRating=0, similarity=0, eps=0;
int i=0, j=0, k=0, count=0, ka=0,scale=0;
u = (double *)malloc(sizeof(double)*m*m);
v = (double *)malloc(sizeof(double)*n*n);
dataMat2 = (double *)malloc(sizeof(double)*m*n);
dataMatCopy = (double *)malloc(sizeof(double)*m*n);
for(i=0;i<m*n;i++)
dataMatCopy[i] = dataMat[i];
for(i=0;i<m*m;i++)
u[i] = 0;
for(i=0;i<n*n;i++)
v[i] = 0;
eps = 0.000001;
ka = max(m,n) + 1;
//奇异值分解
bmuav(&dataMatCopy[0], m, n, u, v, eps, ka);
//挑选合适的奇异值:打印出所有的,再挑选,此处打印略
scale = 4;
I = (double *)malloc(sizeof(double)*scale*scale);
for(i=0;i<scale*scale;i++)
I[i] = 0.0;
for(i = 0;i < scale;i++)
{
I[i*scale+i] = dataMatCopy[i*n+i];
//printf("%f ", I[i*scale+i]);
}
//printf("\n");
//将物品转换到低维空间,data_new = dataMat' * U[:,0:scale] * I
data_new = (double *)malloc(sizeof(double)*n*scale);
svdMat = (double *)malloc(sizeof(double)*n*scale);
matrix_reverse(dataMat, dataMat2, m, n);
brmul(dataMat2, u, n, m, scale, data_new);
brmul(data_new, I, n, scale, scale, svdMat);
for (j = 0;j < n;j++)
{
userRating = dataMat[user*n+j]; //user用户评价过的
if((userRating == 0) || (j == item))
continue;
similarity = simMeas(svdMat, NULL, scale, scale, item, j); //由于是SVD压缩的,不用考虑交集了
simTotal += similarity;
ratSimTotal += similarity * userRating;
}
free(u);free(v);
free(data_new);free(dataMat2);
free(dataMatCopy);free(I);free(svdMat);
if(0 == simTotal)
{
return 0.0;
}else
{
return ratSimTotal/simTotal;
}
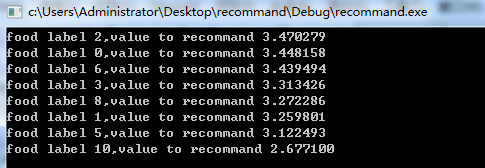
}对于矩阵 data_2,用户2,对应第三行,预测结果:
c. 现实中的挑战
(1)如何对推荐引擎进行评价
我们既没有预测的目标值,也没有用户来调查对他们预测结果的满意度。我们这时可以将已知的评价结果去掉,然后对他们进行预测,最后计算预测值和真实值之间的差异。通常用于推荐引擎评价的指标是最小均方根误差,它 首先计算均方误差的平均值,然后取其平方根 【sqrt((sum((a-b)*(a-b)))/num)】
(2)真实的系统这边代码为了保证可读性,没有效率:
a.我们不必在每次预测评分时都对数据矩阵进行SVD分解。在大规模数据集上,频繁进行SVD分解,只会拖慢效率。在真实系统中,SVD每天运行一次,并且还要离线运行。
b.规模扩展性的挑战:数据矩阵很稀疏,我们有很多0,我们能否只存储非零元素来节省内存计算开销。
相似度计算也导致了计算资源浪费,每次需要一个推荐得分时,都要计算很多物品的相似度得分,这些相似度得分能否被其他用户重复使用?实际系统中,会进行离线计算,并保存相似度得分。
c.如何在缺乏数据时,给出好的推荐?
实际系统将推荐系统看成是搜索问题,我们可能要使用需要推荐物品的属性。在上述餐馆例子里,我们可以通过各种标签来标记菜肴,比如素食、美式烤肉、价格贵等。同时我们也可以将这些属性作为相似度计算所需要的数据。这个被称为基于内容的推荐。
所有代码下载地址:
http://download.csdn.net/detail/jinshengtao/8188243