数据结构面试之十四——字符串的模式匹配
数据结构面试之十四——字符串的模式匹配
题注:《面试宝典》有相关习题,但思路相对不清晰,排版有错误,作者对此参考相关书籍和自己观点进行了重写,供大家参考。
十四、字符串的模式匹配
1. 模式匹配定义——子串的定位操作称为串的模式匹配。
2. 普通字符串匹配BF算法(Brute Force 算法,即蛮力算法)
【算法思想】:
第(1)步;从主串S的第pos个字符和模式的第一个字符进行比较之,若相等,则继续逐个比较后续字符;否则从主串的下一个字符起再重新和模式串的字符比较之。
第(2)步骤;依次类推,直至模式T中的每一个字符依次和主串S中的一个连续的字符序列相等,则称匹配成功;函数值为和模式T中第一个字符相等的字符在主串S中的序号,否则称为匹配不成功,函数值为0。
比如对于主串S=”abacababc”; 模式串T=”abab”; 匹配成功,返回4。
对于主串S=”abcabcabaac”; 模式串T=”abab”; 匹配不成功,返回0。
【算法实现】:
//普通字符串匹配算法的实现
int Index(char* strS, char* strT, int pos)
{
//返回strT在strS中第pos个字符后出现的位置。
int i = pos;
int j = 0;
int k = 0;
int lens = strlen(strS);
int lent = strlen(strT);
while(i < lens && j < lent)
{
if(strS[i+k] == strT[j])
{
++j; //模式串跳步
++k; //主串(内)跳步
}
else
{
i = i+1;
j=0; //指针回溯,下一个首位字符
k=0;
}
}//end i
if(j >= lent)
{
return i;
}
else
{
return 0;
}
}//end
[算法时间复杂度]:设主串长度为m,模式串的长度为n。一般情况下n<m。
最好时间复杂度:举例,主串S=”ababaababc”; 模式串T=”abab”; 比较次数为n次。时间复杂度为O(n)。
最坏时间复杂度:举例,主串S=”000000000000000000001”(20个0,1个1); 模式串T=”00001”(4个0,1个1);比较次数为17*5次。时间复杂度接近O(m*n)。整个匹配过程需要多次回溯(有16次回溯)。
平均时间复杂度:O(m*n)。
[空间复杂度]:O(1),不需要额外开辟空间存储。
3. KMP算法 ——是一种线性时间复杂的字符串匹配算法,它是对BF算法改进。
[时间复杂度]:O(m+n),即:O(strlen(S) + strlen(T))
[空间复杂度]:O(n),即:O(strlen(T))
【核心思想】:是利用已经得到的部分匹配信息来进行后面的匹配过程。
| 正文t |
t1 |
t2 |
t3 |
|
tm |
|
tn |
| 模式p |
p1 |
p2 |
p3 |
…. |
pm |
|
. |
【next(j)定义】:表示当pi不等于tr时,下一次将pnext[i] 与tr开始继续后继对应字符的比较。
其中next[0]=-1,表明当p0不等于tr时,将从p-1与tr开始继续后继对应字符的比较;显然p-1是不存在的,我们可以将这种情况理解成下一步将从p0与tr+1开始继续后继对应字符的比较。
举例说明1:模式串p=“google”,对应的next[j]={-1,0,0,0,1,0}。
解读:
| g |
设定为-1 |
| o |
字符o之前没有匹配的字符。 |
| o |
字符o(第2个)之前的字符(g,o)不同。 |
| g |
字符g之前的字符(g,o,o)前缀、后缀(如:g与o;go与oo)不匹配。 |
| l |
字符l之前的字符(g,o,o,g)前缀、后缀(如:g与g)相同,返回1。 |
| e |
字符e之前的字符(g,o,o,g,l)前缀、后缀(如:goo与ogl)不同。 |
举例说明2:模式串p=“abaabcaba”,对应的next[j]={-1,0,0,1,1,2,0,1,2}。
【KMP算法实现】:
第一步:求解next数组。
typedef struct
{
char str[100];
int length;
}seqString;
//根据模式t的组成求其对应的next数组。
void getNext(seqString t, int next[])
{
next[0] = -1;
int i = 0;
int j = -1;
while(i < t.length)
{
if(j == -1 || t.str[i] == t.str[j])
{
++i;
++j;
next[i] = j;
}
else
{
j = next[j];
}
}//end while
cout << "next[ "<< t.length << " ]" << endl;
for(i = 0; i < t.length; i++)
{
cout << next[i] << "\t";
}
cout << endl;
}//end
第二步:KMP匹配算法的实现。
//t代表正文源串,p代表模式匹配串,next代表匹配next数组
int kmp(seqString t, seqString p, int next[])
{
int i = 0;
int j = 0;
while(i < t.length && j < t.length)
{
if(j == -1 || t.str[i] == p.str[j])
{
i++;
j++;
}
else
{
j = next[j];
}
}
if(j == p.length)
{
return( i -p.length);
}
else
{
return -1;
}
}
int main()
{
int rtnPos = 0;
seqString strS;
strcpy(strS.str,"goodgoogle"); //源串
strS.length = strlen(strS.str);
seqString strT;
strcpy(strT.str,"abaabcaba"); //模式串
strT.length = strlen(strT.str);
int *pNext = new int[strT.length];
getNext(strT,pNext);
rtnPos = kmp(strS,strT,pNext);
cout << rtnPos << endl; //输出匹配位置
return 0;
}
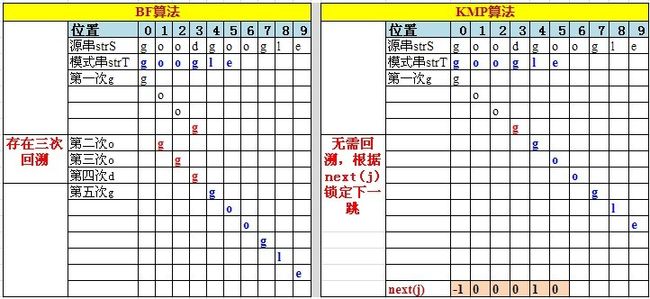
4. 手动演示BF算法与KMP算法的不同(如下图所示)。
字符串的匹配不是很好理解,JULY曾经用很长的篇幅去讲,大家可以参考。很多材料讲的思路一致,但实现稍有差别,本文的实现和图示是一致的,有错误的话希望大家提出,不胜感激!