快速傅立叶变换（FFT）的C++实现与Matlab实验

借佳佳的《复变函数与积分变换》 看了两天，总算弄懂了傅立叶变换是怎么一回事。但是要实现快速傅立叶变换却不需要弄懂那么多东西，看看《算法导论》里面的第 30 章“多项式与快速傅立叶变换”就可以了。不过《算法导论》的介绍和标准的有点小小的不同，就是旋转因子刚好反过来了，不过还是等效的。

标准的离散傅立叶 DFT 变换形式如：

y_k=Σ_j=0^n-1 a_jω_n^-_kj  = A (ω_n^-_k).

（ω_n^k 为复数 1 的第 k 个 n 次方根，且定义多项式 A (x) = Σ_j=0^n-1 a_jx^j ）

而离散傅立叶逆变换 IDFT (Inverse DFT)形式如： a_j=(Σ_k=0^n-1 y_kω_n^kj)/n .

以下不同颜色内容为引用并加以修正：

快速傅立叶变换（Fast Fourier Transform，FFT）是离散傅立叶变换（Discrete Fourier transform，DFT）的快速算法，它是根据离散傅立叶变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅立叶变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。
设 X_n 为 N 项的复数序列，由 DFT 变换，任一 X_i 的计算都需要 N 次复数乘法和 N -1 次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次“运算”（四次实数乘法和四次实数加法），那么求出 N 项复数序列的 X_i ，即 N 点 DFT 变换大约就需要 N² 次运算。当 N =1024 点甚至更多的时候，需要 N² = 1048576 次运算，在 FFT 中，利用 ω_n 的周期性和对称性，把一个 N 项序列（设 N 为偶数），分为两个 N / 2 项的子序列，每个 N / 2点 DFT 变换需要 (N / 2)² 次运算，再用 N 次运算把两个 N / 2点的 DFT 变换组合成一个 N 点的 DFT 变换。这样变换以后，总的运算次数就变成 N + 2 * (N / 2)² = N + N² / 2。继续上面的例子，N =1024 时，总的运算次数就变成了525312 次，节省了大约  50% 的运算量。而如果我们将这种“一分为二”的思想不断进行下去，直到分成两两一组的 DFT 运算单元，那么N 点的 DFT 变换就只需要 N * log₂N 次的运算，N = 1024 点时，运算量仅有 10240 次，是先前的直接算法的1% ，点数越多，运算量的节约就越大，这就是 FFT 的优越性。

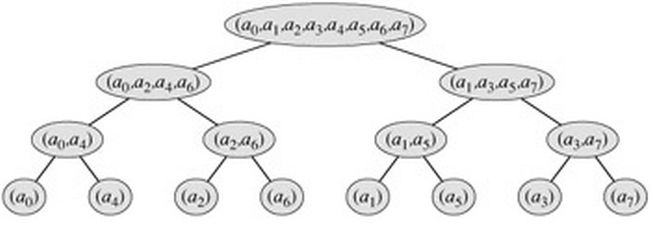
FFT 的实现可以自顶而下，采用递归，但是对于硬件实现成本高，对于软件实现都不够高效，改用迭代较好，自底而上地解决问题。感觉和归并排序的迭代版很类似，不过先要采用“位反转置换”的方法把 X_i 放到合适的位置，设 i 和 j 互为s = log₂N 位二进制的回文数，假设 s = 3,  i = (110)₂  = 6,  j = (011)₂ = 3,  如果 i ≠ j , 那么 X_i 和 X_j 应该互换位置。（关于这个回文数的生成，是很有趣而且是很基本的操作，想当初偶初学 C++ 的时候就有这样的习题。）当“位反转置换”完成后，先将每一个X_i 看作是独立的多项式，然后两个两个地将它们合并成一个多项式（每个多项式有 2 项），合并实际上是“蝶形运算”（Butterfly Operation, 参考《算法导论》吧^_^），继续合并（第二次的每个多项式有 4 项），直到只剩下一个多项式（有 N 项），这样，合并的层数就是 log₂N ，每层都有 N 次操作，所以总共有 N * log₂N 次操作。迭代过程如下图所示，自底而上。

 

 自己写的 C++ 源程序，如下：

/**/ ////////////////////////////////////////////////
//
//  快速傅立叶变换 Fast Fourier Transform
//  By [email protected]
//  2007-07-20
//  版本 2.0
//  改进了《算法导论》的算法，旋转因子取 ω _n ^-_kj  (ω _{n ^kj} 的共轭复数)
//  且只计算 n / 2 次，而未改进前需要计算 (n * lg n) / 2 次。
//  
/**/ ////////////////////////////////////////////////

#include  < stdio.h >
#include  < stdlib.h >
#include  < math.h >

const   int  N  =   1024 ;
const   float  PI  =   3.1416 ;

inline  void  swap ( float   & a,  float   & b)
... {
    float t;
    t = a;
    a = b;
    b = t;
}

void  bitrp ( float  xreal [],  float  ximag [],  int  n)
... {
    // 位反转置换 Bit-reversal Permutation
    int i, j, a, b, p;

    for (i = 1, p = 0; i < n; i *= 2)
        ...{
        p ++;
        }
    for (i = 0; i < n; i ++)
        ...{
        a = i;
        b = 0;
        for (j = 0; j < p; j ++)
            ...{
            b = (b << 1) + (a & 1);    // b = b * 2 + a % 2;
            a >>= 1;        // a = a / 2;
            }
        if ( b > i)
            ...{
            swap (xreal [i], xreal [b]);
            swap (ximag [i], ximag [b]);
            }
        }
}

void  FFT( float  xreal [],  float  ximag [],  int  n)
... {
    // 快速傅立叶变换，将复数 x 变换后仍保存在 x 中，xreal, ximag 分别是 x 的实部和虚部
    float wreal [N / 2], wimag [N / 2], treal, timag, ureal, uimag, arg;
    int m, k, j, t, index1, index2;
    
    bitrp (xreal, ximag, n);

    // 计算 1 的前 n / 2 个 n 次方根的共轭复数 W'j = wreal [j] + i * wimag [j] , j = 0, 1, ... , n / 2 - 1
    arg = - 2 * PI / n;
    treal = cos (arg);
    timag = sin (arg);
    wreal [0] = 1.0;
    wimag [0] = 0.0;
    for (j = 1; j < n / 2; j ++)
        ...{
        wreal [j] = wreal [j - 1] * treal - wimag [j - 1] * timag;
        wimag [j] = wreal [j - 1] * timag + wimag [j - 1] * treal;
        }

    for (m = 2; m <= n; m *= 2)
        ...{
        for (k = 0; k < n; k += m)
            ...{
            for (j = 0; j < m / 2; j ++)
                ...{
                index1 = k + j;
                index2 = index1 + m / 2;
                t = n * j / m;    // 旋转因子 w 的实部在 wreal [] 中的下标为 t
                treal = wreal [t] * xreal [index2] - wimag [t] * ximag [index2];
                timag = wreal [t] * ximag [index2] + wimag [t] * xreal [index2];
                ureal = xreal [index1];
                uimag = ximag [index1];
                xreal [index1] = ureal + treal;
                ximag [index1] = uimag + timag;
                xreal [index2] = ureal - treal;
                ximag [index2] = uimag - timag;
                }
            }
        }
}

void   IFFT ( float  xreal [],  float  ximag [],  int  n)
... {
    // 快速傅立叶逆变换
    float wreal [N / 2], wimag [N / 2], treal, timag, ureal, uimag, arg;
    int m, k, j, t, index1, index2;
    
    bitrp (xreal, ximag, n);

    // 计算 1 的前 n / 2 个 n 次方根 Wj = wreal [j] + i * wimag [j] , j = 0, 1, ... , n / 2 - 1
    arg = 2 * PI / n;
    treal = cos (arg);
    timag = sin (arg);
    wreal [0] = 1.0;
    wimag [0] = 0.0;
    for (j = 1; j < n / 2; j ++)
        ...{
        wreal [j] = wreal [j - 1] * treal - wimag [j - 1] * timag;
        wimag [j] = wreal [j - 1] * timag + wimag [j - 1] * treal;
        }

    for (m = 2; m <= n; m *= 2)
        ...{
        for (k = 0; k < n; k += m)
            ...{
            for (j = 0; j < m / 2; j ++)
                ...{
                index1 = k + j;
                index2 = index1 + m / 2;
                t = n * j / m;    // 旋转因子 w 的实部在 wreal [] 中的下标为 t
                treal = wreal [t] * xreal [index2] - wimag [t] * ximag [index2];
                timag = wreal [t] * ximag [index2] + wimag [t] * xreal [index2];
                ureal = xreal [index1];
                uimag = ximag [index1];
                xreal [index1] = ureal + treal;
                ximag [index1] = uimag + timag;
                xreal [index2] = ureal - treal;
                ximag [index2] = uimag - timag;
                }
            }
        }

    for (j=0; j < n; j ++)
        ...{
        xreal [j] /= n;
        ximag [j] /= n;
        }
}

void  FFT_test ()
... {
    char inputfile [] = "input.txt";    // 从文件 input.txt 中读入原始数据
    char outputfile [] = "output.txt";    // 将结果输出到文件 output.txt 中
    float xreal [N] = ...{}, ximag [N] = ...{};
    int n, i;
    FILE *input, *output;

    if (!(input = fopen (inputfile, "r")))
        ...{
        printf ("Cannot open file. ");
        exit (1);
        }
    if (!(output = fopen (outputfile, "w")))
        ...{
        printf ("Cannot open file. ");
        exit (1);
        }
        
    i = 0;
    while ((fscanf (input, "%f%f", xreal + i, ximag + i)) != EOF)
        ...{
        i ++;
        }
    n = i;    // 要求 n 为 2 的整数幂
    while (i > 1)
        ...{
        if (i % 2)
            ...{
            fprintf (output, "%d is not a power of 2! ", n);
            exit (1);
            }
        i /= 2;
        }

    FFT (xreal, ximag, n);
    fprintf (output, "FFT:    i     real imag ");
    for (i = 0; i < n; i ++)
        ...{
        fprintf (output, "%4d    %8.4f    %8.4f ", i, xreal [i], ximag [i]);
        }
    fprintf (output, "================================= ");

    IFFT (xreal, ximag, n);
    fprintf (output, "IFFT:    i     real imag ");
    for (i = 0; i < n; i ++)
        ...{
        fprintf (output, "%4d    %8.4f    %8.4f ", i, xreal [i], ximag [i]);
        }

    if ( fclose (input))
        ...{
        printf ("File close error. ");
        exit (1);
        }
    if ( fclose (output))
        ...{
        printf ("File close error. ");
        exit (1);
        }
}

int  main ()
... {
    FFT_test ();

    return 0;
}

 

 

/**************************************************

////////////////////////////////////////////////
// sample: input.txt
////////////////////////////////////////////////

    0.5751         0
    0.4514         0
    0.0439         0
    0.0272         0
    0.3127         0
    0.0129         0
    0.3840         0
    0.6831         0
    0.0928         0
    0.0353         0
    0.6124         0
    0.6085         0
    0.0158         0
    0.0164         0
    0.1901         0
    0.5869         0

////////////////////////////////////////////////
// sample: output.txt
////////////////////////////////////////////////
FFT:
   i           real         imag
   0      4.6485      0.0000
   1      0.0176      0.3122
   2      1.1114      0.0429
   3      1.6776     -0.1353
   4     -0.2340      1.3897
   5      0.3652     -1.2589
   6     -0.4325      0.2073
   7     -0.1312      0.3763
   8     -0.1949      0.0000
   9     -0.1312     -0.3763
  10     -0.4326     -0.2073
  11      0.3652      1.2589
  12     -0.2340     -1.3897
  13      1.6776      0.1353
  14      1.1113     -0.0429
  15      0.0176     -0.3122
=================================
IFFT:
   i           real         imag
   0      0.5751     -0.0000
   1      0.4514      0.0000
   2      0.0439     -0.0000
   3      0.0272     -0.0000
   4      0.3127     -0.0000
   5      0.0129     -0.0000
   6      0.3840     -0.0000
   7      0.6831      0.0000
   8      0.0928      0.0000
   9      0.0353     -0.0000
  10      0.6124      0.0000
  11      0.6085      0.0000
  12      0.0158      0.0000
  13      0.0164      0.0000
  14      0.1901      0.0000
  15      0.5869     -0.0000


**************************************************/

使用 Matlab 可以很方便地进行 DFT （Matlab 本身已经提供了实现），以下是在 Matlab 里面的命令行及计算结果。其中 “>>”后面接着命令行，“%”后面接着注释。

>> x = rand (4)   %随机生成 4 * 4 的矩阵，元素不小于 0， 不大于 1

x =

    0.5751    0.3127    0.0928    0.0158
    0.4514    0.0129    0.0353    0.0164
    0.0439    0.3840    0.6124    0.1901
    0.0272    0.6831    0.6085    0.5869

>> x = reshape (x, 16, 1)   %将该矩阵转化成列向量，作为时域离散信号

x =

    0.5751
    0.4514
    0.0439
    0.0272
    0.3127
    0.0129
    0.3840
    0.6831
    0.0928
    0.0353
    0.6124
    0.6085
    0.0158
    0.0164
    0.1901
    0.5869

>> Mn = dftmtx (length (x));   %产生 DFT 矩阵
>> Fx = Mn * x                     %矩阵乘法，等效于 DFT 运算

Fx =

   4.6485         
   0.0176 + 0.3122i
   1.1116 + 0.0427i
   1.6777 - 0.1353i
  -0.2339 + 1.3898i
   0.3651 - 1.2589i
  -0.4325 + 0.2072i
  -0.1312 + 0.3763i
  -0.1950         
  -0.1312 - 0.3763i
  -0.4325 - 0.2072i
   0.3651 + 1.2589i
  -0.2339 - 1.3898i
   1.6777 + 0.1353i
   1.1116 - 0.0427i
   0.0176 - 0.3122i

>> ％以上两句命令可以用这句命令代替：Fx = fft (x,16)   %直接使用 Matlab 内置的 FFT 函数

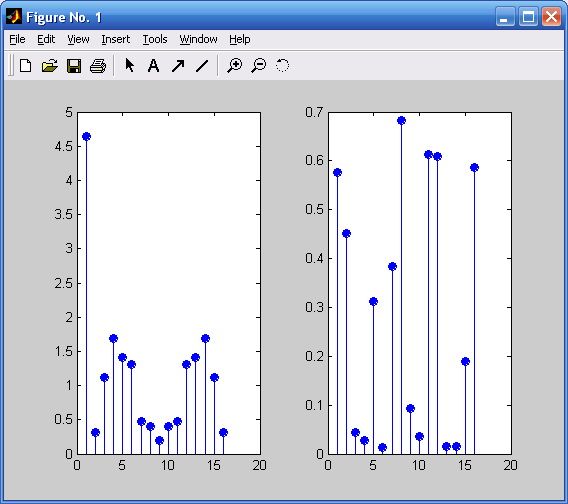
>> % Fx 是离散频域信号，以下四行命令用于画图，如下图所示，左子图为时域信号，右子图为频域信号
>> subplot (1, 2, 1);
>> stem (x, 'fill');
>> subplot (1, 2, 2);
>> stem (abs (Fx), 'fill');

>>
>> Mn2 = inv (Mn);   %产生 DFT 矩阵的逆矩阵，或者 Mn2 = conj(dftmtx(4))/4;
>> x2 = Mn2 * Fx      %矩阵乘法，等效于 IDFT 运算

x2 =

   0.5751 - 0.0000i
   0.4514 + 0.0000i
   0.0439 + 0.0000i
   0.0272 + 0.0000i
   0.3127 + 0.0000i
   0.0129 + 0.0000i
   0.3840 - 0.0000i
   0.6831 + 0.0000i
   0.0928 - 0.0000i
   0.0353 - 0.0000i
   0.6124 - 0.0000i
   0.6085 + 0.0000i
   0.0158 - 0.0000i
   0.0164 - 0.0000i
   0.1901 + 0.0000i
   0.5869 - 0.0000i

>> ％以上两句命令可以用这句命令代替：x2 = ifft (Fx,16)   %直接使用 Matlab 内置的 IFFT 函数

>> % x2 是逆变换回来的离散时域信号，和 x 对比，发现一致， x 中隐含的虚部为 0

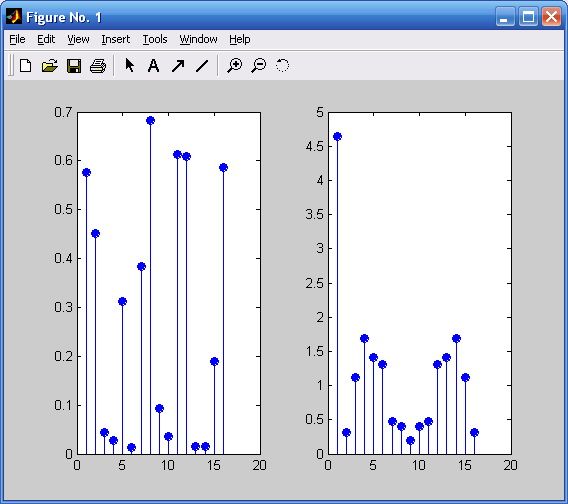
>> % 以下四行命令用于画图，如下图所示，左子图为频域信号，右子图为时域信号
>> subplot (1, 2, 1);
>> stem (abs (Fx), 'fill');
>> subplot (1, 2, 2);
>> stem (abs (x2), 'fill');

>> exit   %退出 Matlab

 对比 C++  程序和  Matlab 的结果，相对误差极小，不知是  C++ 的运算不够精确 （为了使用 fscanf 和 fprintf ，貌似它们不支持 double 类型的，所以我用了 float 类型 ）还是  Matlab 的运算次数太多导致误差累积过多呢？花了一天的时间来完成这个程序，成就感还是挺强烈的，不过偶好累哦。