一起talk C栗子吧(第五十五回:C语言实例--图的最短路径三)
各位看官们,大家好,上一回中咱们说的是使用迪杰斯特拉(Dijkstra)算法计算最短路径的例子,这一回
咱们继续说最短路径的例子:使用弗洛伊德(Floyd)算法计算图的最短路径。闲话休提,言归正转。让我
们一起talk C栗子吧!
看官们,在说弗洛伊德(Floyd)算法前 ,我们说一些关于邻接矩阵的知识。
图的邻接矩阵本质上是二维数组,二维数组中元素的值表示图中顶点之间有一条边,或者该边上的权值。例
如:a[3][6]=1,在不带权图中表示编号为3和6的顶点之间有一条边,该边没有权值;而在带权图中表示编号
为3和6的顶点之间有一条边,而且该边的权值为5。
二维数组中某行元素的值表示位于该行的顶点与其它顶点之间有一条边,或者边上的权值。我们也可以换一种
说法来说:某行元素的值表示把位于该行的顶点当作起点,从起点开始到其它顶点之间的权值。例如:a[3][y]=1,2,0...表示编号为3的顶点与其它顶点之间有一条边,而且边上的权值依次为1,2,0...(与顶点自己的权值为0)。或者说
以编号为3的顶点为起点,从起点到其它顶点的权值为依次为1,2,0...(与顶点自己的权值为0)。
二维数组中某列元素的值表示图中其它顶点与位于该列的顶点之间有一条边,或者边上的权值。我们也可以换
一种说法来说:某列元素的值表示把位于该列的顶点当作终点,从其它顶点开始到终点之间的权值(这里与行
的意义不同)。例如:a[x][3]=1,2,0...表示其它顶点到编号为3的顶点之间有一条边,而且边上的权值依次为1,2,0
(与顶点自己的权值为0)。或者说以编号为3的顶点为终点,从其它顶点到终点的权值为依次为1,2,0...(与顶点自
己的权值为0)。
我们理解邻接矩阵的这些知识后,就为理解弗洛伊德算法打下了基础,接下来我们介绍弗洛伊德算法。
弗洛伊德算法的基本思路:
我们在前面的章回中说过“两点之间的权值不一定是这两点之间的最小权值,可能通过其它中转点找到两点
之间的最小权值。”弗洛伊德算法就是利用了这个思想,在计算图中两个顶点之间的距离时,以图中的其它
顶点作为中转点,计算两点之间的最短路径。如果两个顶点之间的直接距离比经过中转点后两顶点的间接距
离远,那么就把两个顶点之间的间接距离当作两个顶点的最短路径。
弗洛伊德和实现步骤:
- 1.从图中选取一个顶点当作中转点;
- 2.从图中任意选取两个顶点,计算它们之间的最短路径;
- 3.判断两个顶点之间的直接距离与经过中转点后的间接距离;
- 4.如果间接距离比直接距离短,那么更新这两个顶点的最短路径;
- 5.重复步骤1到5.直到图中所有顶点都被当作过中转点为止;
看官们,正文中就不写代码了,详细的代码放到了我的资源中,大家可以点击这里下载使用。关于该程序
我做以下的说明,方便大家理解:
- 1.程序中使用了一个二维数组来存放最短路径的计算结果;二维数组中元素的值表示图中顶点之间最短路径。例如:a[3][6]=1表示编号为3和6的顶点之间的最短路径为1。
- 2.程序中计算出了图中任意两个顶点之间的最短路径;
- 3.程序中计算最短路径时,各个顶点的权值都是正数,如果有某个权值是负数,那么该算法就无能为力了。因此,在使用该算法时需要注意这点。
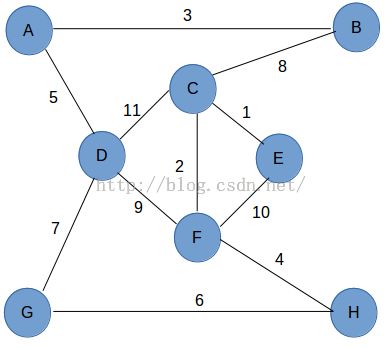
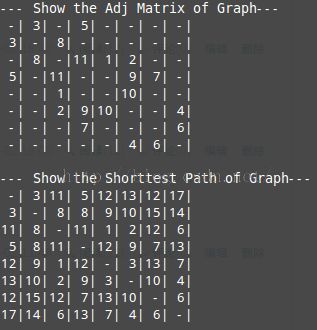
下面是程序的运行结果以及程序中使用的图。
(程序中使用的图) (程序的运行结果)
从程序运行结果中可以看到,顶点A到其它顶点的距离为A->B:3,A->C:11依此类推,A->H:17.顶点到自己的
最短路径为0,为了美观在运行结果中使用“-"表示。大家可以通过对比的方式查看程序运行结果和截图,这
样可以更好地理解程序的原理。
各位看官,关于最短路径的例子咱们就说到这里。欲知后面还有什么例子,且听下回分解。