数据挖掘-基于Kmeans算法、MBSAS算法及DBSCAN算法的newsgroup18828文本聚类器的JAVA实现(下)

本文接数据挖掘-基于Kmeans算法、MBSAS算法及DBSCAN算法的newsgroup18828文本聚类器的JAVA实现(上).

(update 2012.12.28 关于本项目下载及运行的常见问题 FAQ见 newsgroup18828文本分类器、文本聚类器、关联分析频繁模式挖掘算法的Java实现工程下载及运行FAQ )

本文要点如下：

介绍基于LSI(隐性语义索引)中SVD分解做特征降维的方法

介绍两外两种文本聚类算法MBSAS算法及DBSCAN算法

对比三种算法对newsgroup18828文档集的聚类效果

1、SVD分解降维

    以词项(terms)为行, 文档(documents)为列做一个大矩阵(matrix). 设一共有t行d列, 矩阵名为A. 矩阵的元素为词项的tf-idf值。然后对该矩阵做SVD分解  A=T*S*D‘，把S的m个对角元素的前k个保留（最大的k个保留）, 后m-k个置0, 我们可以得到一个新的近似的分解: Xhat=T*S*D’ 。Xhat在最小二乘意义下是X的最佳近似

给定矩阵A, 基于A可以问三类同文件检索密切有关的问题
术语i和j有多相似? 
即术语的类比和聚类问题
文件i和j有多相似?
即文件的类比和聚类问题
术语i和文件j有多相关?
即术语和文件的关联问题

利用SVD分解得到的矩阵可以计算这三个问题，方法如下（DT代表D的转置，以此类推）

比较两个术语  
做"正向"乘法:
Xhat*XhatT=T*S*DT*D*S*TT=T*S2*TT=(TS)*(TS)T
DT*D=I, 因为D已经是正交归一的 ,s=sT
它的第i行第j列表明了术语i和j的相似程度

比较两个文件做"逆向"乘法:
XhatT*Xhat=D*S*TT*T*S*DT=D*S2*DT=(DS)(DS)T
TT*T=I, 因为T已经是正交归一的, s=sT
它的第i行第j列表明了文件i和j的相似程度
此法给出了求文件之间相似度的一个途径，于是可以基于此相似度矩阵实现K-means算法

比较一个文件和一个术语恰巧就是Xhat本身. 
它的第i行第j列表明了术语i和文件j的相关联程度.

SVD分解主要基于JAMA矩阵运算包实现，JAMA矩阵运算包下载见http://math.nist.gov/javanumerics/jama/

DimensionReduction.java

package com.pku.yangliu;

import java.io.IOException;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;

import Jama.Matrix;
import Jama.SingularValueDecomposition;

/**基于LSI对文档的特征向量做降维，SVD运算基于JAMA矩阵运算包实现
 *
 */
public class DimensionReduction {

	/**把测试样例的map转化成文档相似性矩阵
	 * @param Map<String, Map<String, Double>> allTestSampleMap 所有测试样例的<文件名，向量>构成的map
	 * @param String[] terms 特征词集合
	 * @return double[][] doc-doc相似性矩阵
	 * @throws IOException 
	 */
	public double[][] getSimilarityMatrix(
			Map<String, Map<String, Double>> allTestSampleMap, String[] terms) {
		// TODO Auto-generated method stub
		System.out.println("Begin compute docTermMatrix!");
		int i = 0;
		double [][] docTermMatrix = new double[allTestSampleMap.size()][terms.length];
		Set<Map.Entry<String, Map<String,Double>>> allTestSampleMapSet = allTestSampleMap.entrySet();
		for(Iterator<Map.Entry<String, Map<String,Double>>> it = allTestSampleMapSet.iterator();it.hasNext();){
			Map.Entry<String, Map<String,Double>> me = it.next();	
			for(int j = 0; j < terms.length; j++){
				if(me.getValue().containsKey(terms[j])){
					docTermMatrix[i][j] = me.getValue().get(terms[j]);
				}
				else {
					docTermMatrix[i][j] =0;
				}
			}
			i++;	
		}
	    double[][] similarityMatrix = couputeSimilarityMatrix(docTermMatrix);
		return similarityMatrix;
	}

	/**基于docTermMatrix生成相似性矩阵
	 * @param double[][] docTermMatrix doc-term矩阵
	 * @return double[][] doc-doc相似性矩阵
	 * @throws IOException 
	 */
	private double[][] couputeSimilarityMatrix(double[][] docTermMatrix) {
		// TODO Auto-generated method stub
		System.out.println("Compute docTermMatrix done! begin compute SVD");
		Matrix docTermM = new Matrix(docTermMatrix);
		SingularValueDecomposition s = docTermM.transpose().svd();
		System.out.println(" Compute SVD done!");
		//A*A' = D*S*S'*D'   如果是doc-term矩阵
		//A'*A = D*S'*S*D'   如果是term-doc矩阵
		//注意svd函数只适合行数大于列数的矩阵，如果行数小于列数，可对其转置矩阵做SVD分解
		Matrix D = s.getU();
		Matrix S = s.getS();
		for(int i = 100; i < S.getRowDimension(); i++){//降到100维
			S.set(i, i, 0);
		}
		System.out.println("Compute SimilarityMatrix done!");
		return D.times(S.transpose().times(S.times(D.transpose()))).getArray();
	}
}

2、基于SVD分解降维的K-means算法

      有了上面得到的文档与文档之间的相似性矩阵后，我们就可以实现另一个版本的K-means算法了。注意中心点的计算是直接对该聚类中的所有文档的距离向量求平均，作为该中心点与其他所有文档的距离。具体实现如下，主函数在数据挖掘-基于Kmeans算法、MBSAS算法及DBSCAN算法的newsgroup18828文本聚类器的JAVA实现(上)中已经给出。

package com.pku.yangliu;

import java.io.FileWriter;
import java.io.IOException;
import java.util.Iterator;
import java.util.Map;
import java.util.Set;
import java.util.TreeMap;
import java.util.Vector;
import java.lang.Integer;


/**Kmeans聚类算法的实现类，将newsgroups文档集聚成10类、20类、30类,采用SVD分解
 * 算法结束条件:当每个点最近的聚类中心点就是它所属的聚类中心点时，算法结束
 *
 */

public class KmeansSVDCluster {
	
	/**Kmeans算法主过程
	 * @param Map<String, Map<String, Double>> allTestSampleMap 所有测试样例的<文件名，向量>构成的map
	 * @param double [][] docSimilarityMatrix 文档与文档的相似性矩阵 [i,j]为文档i与文档j的相似性度量
	 * @param int K 聚类的数量
	 * @return Map<String,Integer> 聚类的结果  即<文件名，聚类完成后所属的类别标号>
	 * @throws IOException 
	 */
	private Map<String, Integer> doProcess(
			Map<String, Map<String, Double>> allTestSampleMap, double[][] docSimilarityMatrix, int K) {
		// TODO Auto-generated method stub
		//0、首先获取allTestSampleMap所有文件名顺序组成的数组
		String[] testSampleNames = new String[allTestSampleMap.size()];
		int count = 0, tsLength = allTestSampleMap.size();
		Set<Map.Entry<String, Map<String, Double>>> allTestSampeleMapSet = allTestSampleMap.entrySet();
		for(Iterator<Map.Entry<String, Map<String, Double>>> it = allTestSampeleMapSet.iterator(); it.hasNext(); ){
			Map.Entry<String, Map<String, Double>> me = it.next();
			testSampleNames[count++] = me.getKey();
		}
		//1、初始点的选择算法是随机选择或者是均匀分开选择，这里采用后者
		Map<Integer, double[]> meansMap = getInitPoint(testSampleNames, docSimilarityMatrix, K);//保存K个中心点
		//2、初始化K个聚类
		int [] assignMeans = new int[tsLength];//记录所有点属于的聚类序号，初始化全部为0
		Map<Integer, Vector<Integer>> clusterMember = new TreeMap<Integer,Vector<Integer>>();//记录每个聚类的成员点序号
		Vector<Integer> mem = new Vector<Integer>();
		int iterNum = 0;//迭代次数
		while(true){
			System.out.println("Iteration No." + (iterNum++) + "----------------------");
			//3、找出每个点最近的聚类中心
			int[] nearestMeans = new int[tsLength];
			for(int i = 0; i < tsLength; i++){
				nearestMeans[i] = findNearestMeans(meansMap, i);
			}
			//4、判断当前所有点属于的聚类序号是否已经全部是其离得最近的聚类，如果是或者达到最大的迭代次数，那么结束算法
			int okCount = 0;
			for(int i = 0; i <tsLength; i++){
				if(nearestMeans[i] == assignMeans[i]) okCount++;
			}
			System.out.println("okCount = " + okCount);
			if(okCount == tsLength || iterNum >= 25) break;//最大迭代次数1000次
			//5、如果前面条件不满足，那么需要重新聚类再进行一次迭代，需要修改每个聚类的成员和每个点属于的聚类信息
			clusterMember.clear();
			for(int i = 0; i < tsLength; i++){
				assignMeans[i] = nearestMeans[i];
				if(clusterMember.containsKey(nearestMeans[i])){
					clusterMember.get(nearestMeans[i]).add(i);	
				}
				else {
					mem.clear();
					mem.add(i);
					Vector<Integer> tempMem = new Vector<Integer>();
					tempMem.addAll(mem);
					clusterMember.put(nearestMeans[i], tempMem);
				}
			}
			//6、重新计算每个聚类的中心点
			for(int i = 0; i < K; i++){
				if(!clusterMember.containsKey(i)){//注意kmeans可能产生空聚类
					continue;
				}
				double[] newMean = computeNewMean(clusterMember.get(i), docSimilarityMatrix);
				meansMap.put(i, newMean);
			}
		}
		
		//7、形成聚类结果并且返回
		Map<String, Integer> resMap = new TreeMap<String, Integer>();
		for(int i = 0; i < tsLength; i++){
			resMap.put(testSampleNames[i], assignMeans[i]);
		}
		return resMap;
	}

	/**计算新的聚类中心与每个文档的相似度
	 * @param clusterM 该聚类包含的所有文档的序号
	 * @param double [][] docSimilarityMatrix 文档之间的相似度矩阵
	 * @return double[] 新的聚类中心与每个文档的相似度
	 * @throws IOException 
	 */
	private double[] computeNewMean(Vector<Integer> clusterM,
			double [][] docSimilarityMatrix) {
		// TODO Auto-generated method stub
		double sim;
		double [] newMean = new double[docSimilarityMatrix.length];
		double memberNum = (double)clusterM.size();
		for(int i = 0; i < docSimilarityMatrix.length; i++){
			sim = 0;
			for(Iterator<Integer> it = clusterM.iterator(); it.hasNext();){
				sim += docSimilarityMatrix[it.next()][i];
			}
			newMean[i] = sim / memberNum;
		}
		return newMean;
	}

	/**找出距离当前点最近的聚类中心
	 * @param Map<Integer, double[]> meansMap 中心点Map value为中心点和每个文档的相似度
	 * @param int m
	 * @return i 最近的聚类中心的序 号
	 * @throws IOException 
	 */
	private int findNearestMeans(Map<Integer, double[]> meansMap ,int m) {
		// TODO Auto-generated method stub
		double maxSim = 0;
		int j = -1;
		double[] simArray;
		Set<Map.Entry<Integer, double[]>> meansMapSet = meansMap.entrySet();
		for(Iterator<Map.Entry<Integer, double[]>> it = meansMapSet.iterator(); it.hasNext();){
			Map.Entry<Integer, double[]> me = it.next();
			simArray = me.getValue();
			if(maxSim < simArray[m]){
				maxSim = simArray[m];
				j = me.getKey();
			}
		}
		return j;
	}

	/**获取kmeans算法迭代的初始点
	 * @param k 聚类的数量
	 * @param String[] testSampleNames 测试样例文件名数组
	 * @param double[][] docSimilarityMatrix 文档相似性矩阵
	 * @return Map<Integer, double[]> 初始中心点容器 key是类标号，value为该类与其他文档的相似度数组
	 * @throws IOException 
	 */
	private Map<Integer, double[]> getInitPoint(String[] testSampleNames, double[][] docSimilarityMatrix, int K) {
		// TODO Auto-generated method stub
		int i = 0;
		Map<Integer, double[]> meansMap = new TreeMap<Integer, double[]>();//保存K个聚类中心点向量
		System.out.println("本次聚类的初始点对应的文件为：");
		for(int count = 0; count < testSampleNames.length; count++){
			if(count == i * testSampleNames.length / K){
				meansMap.put(i, docSimilarityMatrix[count]);
				System.out.println(testSampleNames[count]);
				i++;
			}
		}
		return meansMap;
	}

	/**输出聚类结果到文件中
	 * @param kmeansClusterResultFile 输出文件目录
	 * @param kmeansClusterResult 聚类结果
	 * @throws IOException 
	 */
	private void printClusterResult(Map<String, Integer> kmeansClusterResult, String kmeansClusterResultFile) throws IOException {
		// TODO Auto-generated method stub
		FileWriter resWriter = new FileWriter(kmeansClusterResultFile);
		Set<Map.Entry<String,Integer>> kmeansClusterResultSet = kmeansClusterResult.entrySet();
		for(Iterator<Map.Entry<String,Integer>> it = kmeansClusterResultSet.iterator(); it.hasNext(); ){
			Map.Entry<String, Integer> me = it.next();
			resWriter.append(me.getKey() + " " + me.getValue() + "\n");
		}
		resWriter.flush();
		resWriter.close();
	}
	
	/**Kmeans算法
	 * @param String testSampleDir 测试样例目录
	 * @param String[] term 特征词数组
	 * @throws IOException 
	 */
	public void KmeansClusterMain(String testSampleDir, String[] terms) throws IOException {
		//首先计算文档TF-IDF向量，保存为Map<String,Map<String,Double>> 即为Map<文件名，Map<特征词，TF-IDF值>>
		ComputeWordsVector computeV = new ComputeWordsVector();
		DimensionReduction dimReduce = new DimensionReduction();
		int[] K = {10, 20, 30};
		Map<String,Map<String,Double>> allTestSampleMap = computeV.computeTFMultiIDF(testSampleDir);
		//基于allTestSampleMap生成一个doc*term矩阵，然后做SVD分解
		double[][] docSimilarityMatrix = dimReduce.getSimilarityMatrix(allTestSampleMap, terms);
		for(int i = 0; i < K.length; i++){
			System.out.println("开始聚类，聚成" + K[i] + "类");
			String KmeansClusterResultFile = "F:/DataMiningSample/KmeansClusterResult/";
			Map<String,Integer> KmeansClusterResult = new TreeMap<String, Integer>();
			KmeansClusterResult = doProcess(allTestSampleMap, docSimilarityMatrix, K[i]);
			KmeansClusterResultFile += K[i];
			printClusterResult(KmeansClusterResult,KmeansClusterResultFile);
			System.out.println("The Entropy for this Cluster is " + computeV.evaluateClusterRes(KmeansClusterResultFile, K[i]));
		}
	}
}

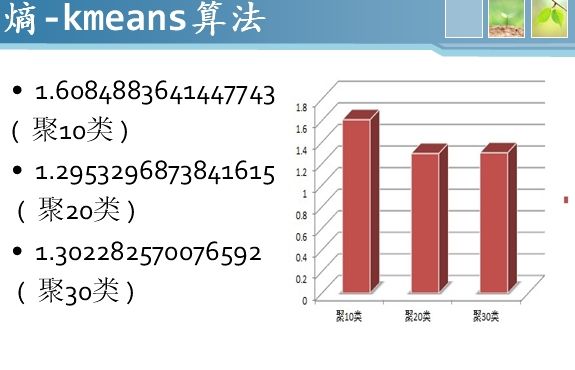
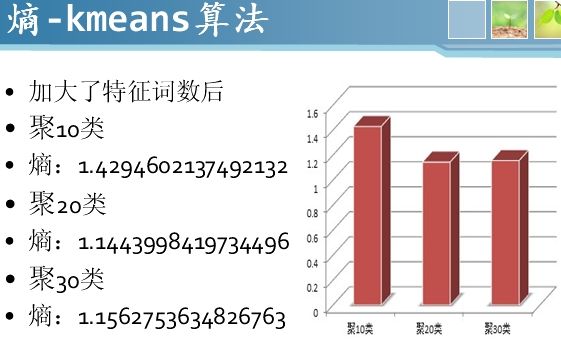
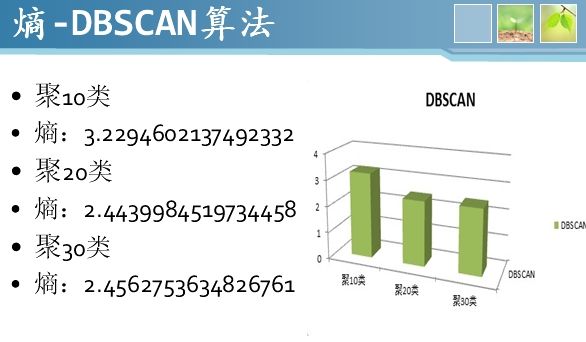
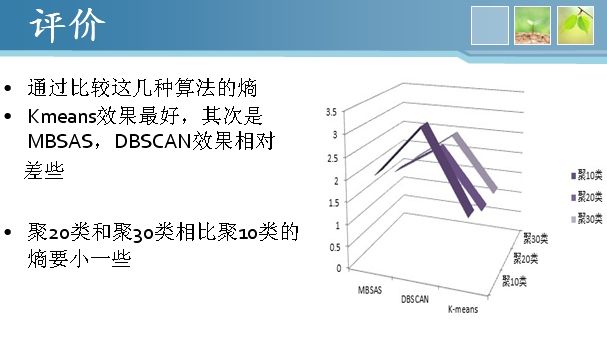
3、K-means算法、MBSAS算法、DBSCAN算法三种算法的聚类结果对比

     另外两种聚类算法MBSAS算法和DBSCAN算法由我们组另外两位同学实现，其实也很简单，源码这里就不贴出来了。感兴趣的朋友可以到点击打开链接下载eclipse工程运行。这三种算法的聚类结果采用熵值大小来评价，熵值越小聚类效果越好，具体如下

可见对newsgroup文档集聚类采用K-means算法，用余弦相似度或者内积度量相似度可以达到良好的效果。而SVD分解还是很耗时间，事实上对20000X3000的矩阵做SVD分解的时间慢得难以忍受，我还尝试对小规模数据聚类，但是发现降维后聚类结果熵值超过了2，不及DF法降维的聚类效果。因此对于文本聚类的SVD降维未必是好方法,。除了这三种聚类算法，还有层次聚类算法等其他很多算法，以后会尝试给出其他算法的实现和聚类效果对比。敬请关注:)