[置顶] 模式识别、推荐系统中常用的两种矩阵分解-----奇异值分解和非负矩阵分解
第一部分:矩阵的奇异值分解:
矩阵的奇异值分解证明过程中会用到五个定理,先作为补充知识展示这五个定理:
定理一:A是对称矩阵,则不同特征值对应的特征向量是正交的。
证明:设![]() ,
,![]() 是矩阵A的特征向量,且
是矩阵A的特征向量,且![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() 对应的特征向量,即:
对应的特征向量,即:
![]() ,
,![]()
则
![]() ,
,![]()
因为A是对称矩阵,则
![]()
所以,
![]()
则:
![]()
因为
![]() ,
,
所以:
![]() ,
,
即:![]() 和
和![]() 是正交的。证毕
是正交的。证毕
————————————————————————————————————————————————————————————————————————————
定理二:矩阵![]() 和它的转置
和它的转置![]() 具有相同的特征值
具有相同的特征值
证明:因为:
![]() ,
,
即![]() 和
和![]() 有相同的特征多项式,所以有相同的特征值。
有相同的特征多项式,所以有相同的特征值。
————————————————————————————————————————————————————————————————————————————
定理三:半正定矩阵的特征值均大于等于零
证明:这是半正定矩阵的定义
————————————————————————————————————————————————————————————————————————————
定理四:若![]() 满足
满足![]() ,则称
,则称![]() 是单位正交矩阵
是单位正交矩阵
单位正交矩阵有如下的性质:![]() 。
。
————————————————————————————————————————————————————————————————————————————
定理五:若矩阵![]() 的秩为r,则
的秩为r,则![]() 和
和![]() 秩均为r。
秩均为r。
————————————————————————————————————————————————————————————————————————————
补充完以上五个定理,我们正式开始矩阵的奇异值分解的证明。
设矩阵![]() ,矩阵的秩为
,矩阵的秩为![]() ,且
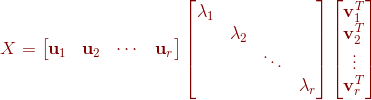
,且![]() ,则矩阵可以分解为如下形式:
,则矩阵可以分解为如下形式:
也可表示为:
证明:无非就是寻找![]() 。
。
显然![]() ,
,![]() ,且这两个矩阵均是半正定矩阵,且互为转置,且根据定理五,这两个矩阵的秩均为
,且这两个矩阵均是半正定矩阵,且互为转置,且根据定理五,这两个矩阵的秩均为![]() 。根据定理二和定理三,这两个矩阵的特征值是相同的,且均大于等于零。我们只用大于零的特征值。设
。根据定理二和定理三,这两个矩阵的特征值是相同的,且均大于等于零。我们只用大于零的特征值。设![]() (我们按从大到小排序即:
(我们按从大到小排序即:![]() )是它们的不为零的特征值,且对于矩阵
)是它们的不为零的特征值,且对于矩阵![]() 对应的单位特征向量为
对应的单位特征向量为![]() (
(![]() ),对于矩阵
),对于矩阵![]() 对应的单位特征向量为
对应的单位特征向量为![]() (
(![]() ),即
),即
![]() ,
,![]() 。
。
其实![]() 和
和![]() 存在一定的关系,下面就找出这种关系。
存在一定的关系,下面就找出这种关系。
因为
![]() ,
,
所以,![]() 是
是![]() 的特征向量,又因为
的特征向量,又因为![]() 也是
也是![]() 的特征向量,所以,
的特征向量,所以,
![]() ,
,
又因为
![]() ,
,
所以:
![]() 。
。
则:
所以,
那么
下面证明
其中![]() 代表单位矩阵。
代表单位矩阵。
因为![]() 是对称矩阵
是对称矩阵![]() 的不同特征值对应的特征向量,根据定理一,我们得出他们是相互正交的,又因为
的不同特征值对应的特征向量,根据定理一,我们得出他们是相互正交的,又因为
然后,然后根据定理四,我们便得到
所以:
证毕。
注:奇异值分解在自然语言处理和推荐系统中有广泛应用,例子我就不敲了,网上很多。矩阵怎么分解都知道了,那它的应用,我想也不是问题。
————————————————————————————————————————————————————————————————————————————
第二部分:非负矩阵分解:
非负矩阵分解的动机:我们知道在矩阵的奇异值分解,特征向量中有可能出现负值,而负值在很多问题中是没有意义的,所以提出了矩阵的非负分解。台湾大学的林老师(Chih-Jen Lin:libsvm的作者)用投影梯度法,讲解了非负矩阵的分解,并给出了源码,虽然我的专业是非线性规划,投影梯度法是明白,但是,对于矩阵函数的矩阵求导,我没弄懂,弄懂之后再补吧,所以,下面只给出python代码的运行步骤(有很多方法,只说一种),因为NMF的python源码需要numpy,所以我们直接用pythonxy。
然后,将你下载的源码放到\.xy\startups文件夹中:出现以下界面
然后,就可以在命令窗口敲入 import nmf,用nmf这个函数了。
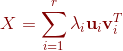
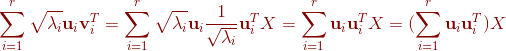
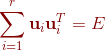
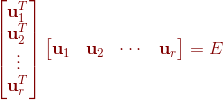
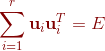
![[置顶] 模式识别、推荐系统中常用的两种矩阵分解-----奇异值分解和非负矩阵分解_第1张图片](http://img.e-com-net.com/image/info5/a5eb573c4d19462e80df657150abb99d.jpg)
![[置顶] 模式识别、推荐系统中常用的两种矩阵分解-----奇异值分解和非负矩阵分解_第2张图片](http://img.e-com-net.com/image/info5/411db81d85464d2ca8c5ce8cc8c46925.jpg)