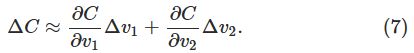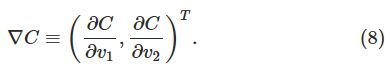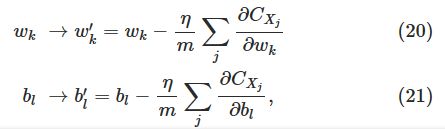神经网络那些事儿(一)
这次主要说说神经网络的一些主要思想,包括介绍两种人工神经元(perceptron neuron和sigmoid neuron)以及神经网络的标准学习算法,随机梯度下降法。神经网络可以认为是一种不同于使用普通计算机语言编程的那种基于规则的编程范型,它从生物中受到启发(人脑),让计算机可以从大量的数据中自动推导和发现规律。这些大量的数据就被称为训练样本,从训练样本中自动推导的过程被称为神经网络的学习。神经网络并不一定是机器学习,但是本文将其看成机器学习的一种方法。
感知机
要说神经网络,首先还是得从感知机说起。感知机由科学家Frank Rosenblatt在1950s和1960s时候开发出来,主要建立在Warren McCulloch和Walter Pitts早期的工作基础上。但是现在感知机神经元已经用得少了,更多的是用其他的神经元模型来代替,比如sigmoid 神经元。
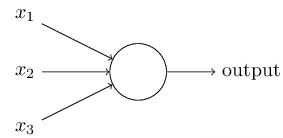
感知机模型如图1所示,输入是二元(只有0,1)的变量,然后输出也是一个二元变量。
图1
那么它的计算规则是啥呢?Rosenblatt引进了权重(weights)![]() 的概念,它们是表示相关输入对于输出值的重要性程度的一些实数。感知机神经元的输出(0或者1)取决于权重的和
的概念,它们是表示相关输入对于输出值的重要性程度的一些实数。感知机神经元的输出(0或者1)取决于权重的和![]() 是小于还是大于某个阀值。这里的阀值同样是一个实数,也是神经元的一个参数。用数学来表示就是:
是小于还是大于某个阀值。这里的阀值同样是一个实数,也是神经元的一个参数。用数学来表示就是:
上面是基础的数学模型。为了理解它,我们可以举一个通俗地例子。(1)式中决定输出的机制主要是通过权衡所有的"证据"。比如周末即将到来,你想要去参加一个活动,所以你需要决定是去还是不去。那么我们可以通过列举一下影响你去还是不去的主要因素,比如说:
-
天气是不是很好?2. 你的男朋友或女朋友是不是愿意陪伴你?3. 交通是不是便利?
然后,我们可以通过给这些因素相应的二元变量![]() 和
和![]() 来表示。例如,
来表示。例如,![]() =1表示天气是好的,
=1表示天气是好的,![]() =0表示天气不好。类似地,
=0表示天气不好。类似地,![]() 和
和![]() 也是同样的道理。
也是同样的道理。
如果你非常想去参加这个活动,所以你不管你男朋友或女朋友感不感兴趣,也不管交通多么不便利,你唯一在意的因素是天气。所以我们可以为这三个因素分别选择一个权重,天气的![]() =6,其他两个因素分别是,
=6,其他两个因素分别是,![]() =2,
=2,![]() =2。最后,假设你选择5作为感知机的阀值。有了这些值,你就可以计算,最终判断你是去还是不去参加活动。你可能发现了,改变权值和阀值我们会得到不同的决策的模型。例如,假设我们选择3作为阀值(刚才是5),那么感知机将决定你应当去参加这个活动,而不管天气多好或者其他两个因素的影响。换句话说就是模型已经变了。"丢弃"阀值意味着你更愿意去参加这个活动。
=2。最后,假设你选择5作为感知机的阀值。有了这些值,你就可以计算,最终判断你是去还是不去参加活动。你可能发现了,改变权值和阀值我们会得到不同的决策的模型。例如,假设我们选择3作为阀值(刚才是5),那么感知机将决定你应当去参加这个活动,而不管天气多好或者其他两个因素的影响。换句话说就是模型已经变了。"丢弃"阀值意味着你更愿意去参加这个活动。
显然,感知机并不是人类决策系统的一个完美模型。但是例子表明了一个感知机是如何权衡不同类型证据来做决策的。把这些神经元组合起来看起来貌似可以作出十分微妙的决策:
这个网络的第一列感知机神经元,我们称之为第一层感知机神经元,它们通过权衡输入"证据作出了3个不同的简单决策,。第二层的感知机神经元权衡了第一层决策的结果的证据。可以看到,第二层的神经元作出的决策比第一层的神经元更加复杂和抽象。
下面将简化描述感知机的方式。条件![]() > threshold看起来是累赘的,并且我们能够改变两个符号从而简化它。第一个变化是把
> threshold看起来是累赘的,并且我们能够改变两个符号从而简化它。第一个变化是把![]() 写成点积的形式,
写成点积的形式,![]() 其中w和x是两个向量,它们的组成(components)分别是权值和输入。第二个变化是把阀值(threshold)移动到不等式的另一边,以及用称为感知机的偏置,b=-threshold来代替。使用偏置来代替阀值,感知机的规则可写成:
其中w和x是两个向量,它们的组成(components)分别是权值和输入。第二个变化是把阀值(threshold)移动到不等式的另一边,以及用称为感知机的偏置,b=-threshold来代替。使用偏置来代替阀值,感知机的规则可写成:
你可以把偏置想成是度量感知机神经元的输出是如何容易地接近1。或者用生物学的术语来说,偏置是度量感知机神经元有多容易被激活。对于一个有很大偏置的感知机,它是极其容易使得神经元输出1。但是,如果偏置是一个非常大的负数,那么它的输出很难是1。引进偏置仅仅是在描述感知机时的一个小的变化,但是它将导致更多的符号上的简化。
我们能够设计学习算法来自动地调整网络中的人工神经元的权值和偏置。这个调整是对外部刺激的回应,而不是一个程序员直接地干预改变。实际上感知机实现的功能与逻辑门一样,但引入学习算法使得我们能够用与传统逻辑门彻底不同的人工神经元。
Sigmoid 神经元
学习算法(learning algorithm)听起来不错。但是怎样为一个神经网络设计这样的算法呢?假设我们使用一个感知机的网络来解决一些问题,例如,网络的输入可能是一个扫描过的,一个手写数字的图像的原生像素数据。我们想要网络学习权值和偏置使得输出能够正确地分类数字。为了看到学习算法(你可以先把学习简单地理解为算法怎样找到好的参数的机制)是如何工作地,假设网络中的某些权重(或偏置)发生了一个很小的改变。我们想要的是权重中的这个很小的变化也能够引起输出的相应的一个小的变化。待会我们将看到,这个性质将使得学习成为可能。可以看看下面的图:
如果这个是真的,即在一个权值(或偏置)上的一个小的变化会引起输出的一个小的变化,那么我们就能够使用这个因素来修改权值和偏置来得到我们想要的神经网络的输出。举个例子,假设网络错误地把本应该是一个"9"的图像分类成了一个"8"的图像。我们能够计算出怎样改变权值和偏置使得网络能够更接近分类图像为一个"9"。然后我们将重复这个过程,不断地改变权值和偏置产生越来越好的输出。这就是神经网络的学习。
问题是当我们的网络包含感知机神经元时,结果并不是像这样。事实上,当任何一个神经元上的权值和偏置上的一个小的变化有时候能够引起那个神经元的输出发生巨大的变化,比如说使得输出直接从0一下子突变成了1。这种大的变化可能会引起网络的其他神经元的行为以一种很复杂的方式完全发生改变。因此,当你的"9"可能现在是分类正确的,但是网络在所有其他图像上的行为可能以一种难以控制的方式改变。这使得很难通过逐渐修改(微调)权值和偏置使得网络越来越接近期望的输出结果。
于是就引进了一种新的神经元类型-sigmoid神经元。它和感知机很类似,但是对权值和偏置的一点小变化能引起输出的一点小变化。而不是像感知机那样使得输出发生了突变(原因在于感知机实际上是一个跃阶函数)。
区别在于sigmoid神经元的输出不是0或者1,而是0和1之间的任何值。比如说,0.638…。同样地,sigmoid神经元的每个输入x也是有权重w和偏置b。那么现在输出变成了![]() ,称为sigmoid函数(还有个名字叫logistic函数),定义为:
,称为sigmoid函数(还有个名字叫logistic函数),定义为:
所以,输入为![]() ,权重为
,权重为![]() 以及偏置为b的sigmoid的神经元的输出为:
以及偏置为b的sigmoid的神经元的输出为:
让我们来看看它和感知机神经元的区别吧。现在假设![]() 是一个很大的正数。那么
是一个很大的正数。那么![]() ,因此
,因此![]() 。换句话说就是,当
。换句话说就是,当![]() 很大而且是正的,那么sigmoid神经元的输出就接近1,就和之前说的感知机一样。另外一方面,我们假设
很大而且是正的,那么sigmoid神经元的输出就接近1,就和之前说的感知机一样。另外一方面,我们假设![]() 是非常小的负数(绝对值大)。那么
是非常小的负数(绝对值大)。那么![]() ,所以
,所以 ![]() 。
。
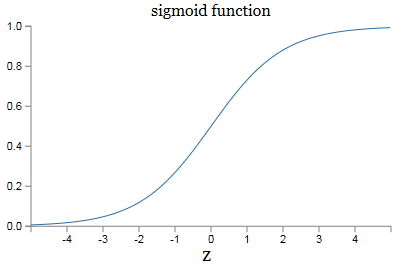
这是sigmoid函数的图像。它可看成是下面的跃阶函数的光滑版本:
如果![]() 是一个跃阶函数(step function),那么sigmoid神经元将是一个感知机,因为输出将要么是1要么是0,这取决于
是一个跃阶函数(step function),那么sigmoid神经元将是一个感知机,因为输出将要么是1要么是0,这取决于![]() 是正的还是负的。通过使用实际的
是正的还是负的。通过使用实际的![]() 函数,我们得到了一个光滑版的感知机。
函数,我们得到了一个光滑版的感知机。![]() 的光滑性意味着权重中的小的变化
的光滑性意味着权重中的小的变化![]() 以及偏置小的变化
以及偏置小的变化![]() 将导致一个输出小的变化
将导致一个输出小的变化![]() 。由微积分知识,我们可以得到输出变化
。由微积分知识,我们可以得到输出变化![]() 可以由下面的式子计算:
可以由下面的式子计算:
我们可以这样来理解这个式子,输出变化![]() 是权值变化
是权值变化![]() 和偏置变化
和偏置变化![]() 的一个线性函数。这种线性关系使得选择权值和偏置中的小的变化更容易达到任何期望的输出变化值。
的一个线性函数。这种线性关系使得选择权值和偏置中的小的变化更容易达到任何期望的输出变化值。
我们该如何解释一个sigmoid神经元的输出?显然,在感知机和sigmoid神经元之间最大的不同是sigmoid神经元不只输出0或者1。它们能够使输出为任何的实数在0和1之间,因此像0.173…和0.689这样的值是正确的输出值。这是很有用的,例如,如果我们想要使用输出值来代表一幅图像输入中像素的平均密度。但是有时候这却也是比较棘手的问题,假设我们想要一个输出来表示是"输入图像是9"或者"输入图像是8"。显然,如果输出是0或者1,就像在感知机中那样的,那么就很容易做到的。但是在实践中我们能够建立一种约定来达到这种目的,例如,通过决定把任何至少是0.5的输出解释为一个"9"的图像,而不任何少于0.5的输出值解释为一个"不是9"的图像。关键是为什么这样可行呢?
神经网络的结构
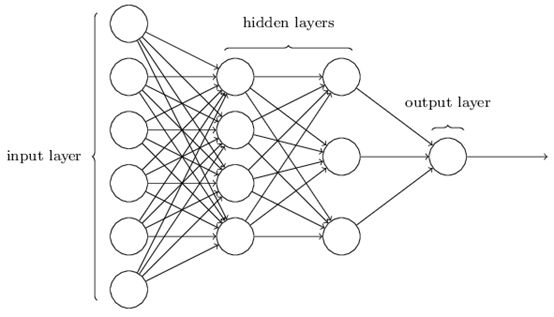
假设我们下面的神经网络:
最左边的被称为输入层,其中的神经元是输入神经元。最右边的是输出层包含了输出神经元。中间的被称为一个隐藏层,称为隐藏层是因为它既不是输入也不是输出,其他没有什么原因了。可以有多个隐藏层:
网络中的输入和输出层的设计通常是简单的。例如,假设我们正在决定一个手写图像是不是一个"9"。一个自然的方式来设计网络就是编码输入图像像素的强度。如果图像是一个64*64灰度级的图像,那么我们就有4096=64 x 64输入神经元,它们的强度级别在0和1之间。输出层将只包含一个单神经元,输出值小于0.5的时候表示输入图像不是一个9,反之是一个9。虽然,输入层和输出层的设计比较直观简单,但是隐藏层的设计就不一样了。研究者们开发了许多设计隐藏层的启发式方法来帮助人们获得它们想要的网络的行为。例如,这样的启发式方法能够被用来帮助决定怎样权衡隐藏层的个数,因为训练网络需要时间。后面我们将会遇到几种这样的设计启发式方法。
目前为止我们讨论的是前向神经网络,因为每一层的输入都是前一层的输出。这意味着网络中没有循环,信息总是前向反馈,从不往后反馈。当然也存在其他的神经网络结构里有前向循环,比如说recurrenct neural networks。这些模型的思想是使神经元被激活持续某段时间,在它变得静止之前。这个激活能够刺激其他的神经元,它们将在之后会被激活,也是一段时间。循环在这种模型中没有导致问题,因为一个神经元输出仅仅影响了它的输入在某个后续时间,而不是即刻被激活。
使用梯度下降来学习
我们用来分类数字的算法首先是要找到使得对于所有的训练输入x,神经网络的输出都接近于y(x)(它是已标记过的手写数字的类别)的那些权值和偏置。为了量化所有训练输入x的输出有多接近y(x),我们定义了一个损失函数:
(y(x)是实际正确的标记过的手写数字的类别,a是神经网络计算出来的类别)。我们把C称为二次损失函数,也有个别名叫均方误差MSE(mean squared error)。现在的目标就是要最小化C,并求出相应的w,b就可以了。有个著名的方法叫梯度下降(gradient descent)。
现在假设我们正在最小化某个函数C(v)。v是个向量,![]() 现在我们考虑两个变量的函数C,我们称之为
现在我们考虑两个变量的函数C,我们称之为![]() 和
和![]() 。这是一个连续多元函数的最小值问题。大家首先会想到积分的方法,我们可以计算偏导数,然后找出C的所有极值点,最后找出最小值点。运气好的话,你遇到的C可能是只有1个或2个变量。但是当我们有许许多多地变量呢?(神经网络中几十亿个权值和偏置都是有可能的!)所以使用积分的方法是不可行的。
。这是一个连续多元函数的最小值问题。大家首先会想到积分的方法,我们可以计算偏导数,然后找出C的所有极值点,最后找出最小值点。运气好的话,你遇到的C可能是只有1个或2个变量。但是当我们有许许多多地变量呢?(神经网络中几十亿个权值和偏置都是有可能的!)所以使用积分的方法是不可行的。
于是前辈们提出了梯度下降的方法。可以举一个通俗的例子来理解这个算法,我们把这个需要寻找最小值的函数想象成一个山谷,想象有一个球从斜坡上滚下来,经验告诉我们这个球最终会滚到山谷的底部。我们可以借助这个思想来寻找函数的最小值。随机地选择一个点,让小球从这个点往下滚,但是我们的算法并不是严格按照这个模型来进行,因为小球在现实生活中是受重力影响往下滚的,而我们的算法并不考虑这个。所以它是忽略了一些条件,假设把小球沿着![]() 方向移动一个很小的量
方向移动一个很小的量![]() ,在
,在![]() 方向上移动另一个很小的量
方向上移动另一个很小的量![]() 。微积分的知识告诉我们损失函数C(含有二个变量v1和v2)的变化如下:
。微积分的知识告诉我们损失函数C(含有二个变量v1和v2)的变化如下:
记住我们的目的是使C值最小,所以C的变化![]() 如果是负的,就说明C在减小,也就是这个球正在往山谷下面滚。关键是如何找到选择
如果是负的,就说明C在减小,也就是这个球正在往山谷下面滚。关键是如何找到选择![]() 和
和![]() 的方式呢?为了方便描述,我们引进一个新的变量
的方式呢?为了方便描述,我们引进一个新的变量![]() ,然后定义C的梯度为偏导数向量,
,然后定义C的梯度为偏导数向量,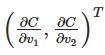 。我们用
。我们用![]() 表示梯度,也就是:
表示梯度,也就是:
所以我们重写损失函数C的变化为:
问题变成了如何选择![]() 来使得
来使得![]() 为负数。前辈们是这样构造的,令:
为负数。前辈们是这样构造的,令:
这里的![]() 是较小的,正的参数(它有个好听的名字叫学习率)。等式(9)告诉我们:
是较小的,正的参数(它有个好听的名字叫学习率)。等式(9)告诉我们:
![]()
现在我们发现![]() ,这就保证了
,这就保证了![]() ,也就是C将总是在减小,从不会增加,到现在我们也就知道了怎样选择v,即,我们使用等式(10)来计算
,也就是C将总是在减小,从不会增加,到现在我们也就知道了怎样选择v,即,我们使用等式(10)来计算![]() 的一个值,然后沿着v方向把小球移动一个量:
的一个值,然后沿着v方向把小球移动一个量:
接下来再次使用这个更新规则来继续小球的另外一个增量的移动,我们不断地保持这样做,那么将保持减少C直到我们达到一个全局最小值。总的来说,梯度下降算法的工作原理就是重复地计算梯度![]() ,然后在其相反的方向移动,使得小球沿着山谷向下走。用图形来看就是:
,然后在其相反的方向移动,使得小球沿着山谷向下走。用图形来看就是:
为了使梯度下降正确地工作,我们需要选择足够小地学习率![]() 使得等式(9)是一个好的近似。如果我们没有这样做,可能最终会以
使得等式(9)是一个好的近似。如果我们没有这样做,可能最终会以![]() 结束(不要怀疑这一点),这显然不是我们想要的结果。同时,我们也不希望选择太小的学习率,因为这将获得一个很小的
结束(不要怀疑这一点),这显然不是我们想要的结果。同时,我们也不希望选择太小的学习率,因为这将获得一个很小的![]() 变化,将导致梯度下降算法工作地非常慢。在实践中,
变化,将导致梯度下降算法工作地非常慢。在实践中,![]() 通常是不一样的,使得等式(9)保持一个好的近似,但是算法也不能太慢。后面我们将看到怎么选取学习率
通常是不一样的,使得等式(9)保持一个好的近似,但是算法也不能太慢。后面我们将看到怎么选取学习率![]() 。刚才已经解释了当C是一个只有2个变量的函数的梯度下降,事实上对于多个变量也是差不多的,只是把v向量的维数增加一下。梯度下降算法的更新规则总是这样的:
。刚才已经解释了当C是一个只有2个变量的函数的梯度下降,事实上对于多个变量也是差不多的,只是把v向量的维数增加一下。梯度下降算法的更新规则总是这样的:
但是,这个规则并不总是正确工作,有一些情况会导致错误以及阻止梯度下降找到C的全局最小值,后面会提到这个问题。不过,不用担心,梯度下降通常在实践中都工作得很好,在神经网络中我们将发现它是最有力的最小化损失函数的一种来帮助网络学习的方式。
实际上,梯度下降是一种寻找最小值的策略。假设我们尝试在某个方向上移动![]() 来尽可能多地减小C。这就等价于最小化
来尽可能多地减小C。这就等价于最小化![]() 。我们将限制移动的步长大小为:
。我们将限制移动的步长大小为:![]() 对于某个小的固定的
对于某个小的固定的![]() 。换句话说,我们想要一个是固定步长的移动,以及我们尝试找到尽可能多地减小C的移动方向。可以被证明最小化的
。换句话说,我们想要一个是固定步长的移动,以及我们尝试找到尽可能多地减小C的移动方向。可以被证明最小化的![]() 是
是![]() 。
。
接下来的问题就是如何把梯度下降应用到一个神经网络中呢?目的还是找到使得等式(6)中的损失函数最小的权值![]() 和偏置
和偏置![]() 。也就是把刚才的
。也就是把刚才的![]() 换成权值
换成权值![]() 和偏置
和偏置![]() ,换句话说就是现在梯度向量变成了:
,换句话说就是现在梯度向量变成了:![]() 和
和![]() 。所以梯度下降规则就变成了:
。所以梯度下降规则就变成了:
只要重复应用这个规则就能使"小球往山下移动"以及找到损失函数的一个最小值。应用梯度下降规则存在很多挑战,后面会深入分析这个问题。现在只提一个问题。我们注意到损失函数有形式![]() ,即它是单个训练样本的损失
,即它是单个训练样本的损失![]() 的一个平均值。在实践中,为了计算梯度
的一个平均值。在实践中,为了计算梯度![]() 我们需要单独地为每个训练输入x计算梯度,然后算出它们的平均值,
我们需要单独地为每个训练输入x计算梯度,然后算出它们的平均值,![]() 。不幸地是,当训练输入的个数很大的时候,这将十分耗费时间,这会导致学习地很慢。
。不幸地是,当训练输入的个数很大的时候,这将十分耗费时间,这会导致学习地很慢。
于是出现了另外一种想法,叫随机梯度下降,它是用来加速学习的。主要想法就是通过计算
随机选择出来的训练输入的这个小样本的![]() ,这将帮助加速梯度下降,从而提高算法的学习速度。更精确地说,随机梯度下降通过随机挑选出m(相对小的)个随机选择的训练输入。我们标记这些随机训练输入为
,这将帮助加速梯度下降,从而提高算法的学习速度。更精确地说,随机梯度下降通过随机挑选出m(相对小的)个随机选择的训练输入。我们标记这些随机训练输入为![]() 并且给它们取个新的名字叫mini-batch。问题是这个m我们选多少最为合适呢?我们期望
并且给它们取个新的名字叫mini-batch。问题是这个m我们选多少最为合适呢?我们期望![]() 的平均值能够粗糙地等于全部所有的
的平均值能够粗糙地等于全部所有的![]() 的平均,即:
的平均,即:
其中第2个和是训练数据的全部集合。交换一下顺序就会得到:
我们能够通过计算仅仅是随机选择的mini-batch的梯度来估计全部的梯度。所以现在我们的基于随机梯度下降方法的神经网络的梯度更新规则就变成了:
其中的和是当前mini-batch中的所有训练样本![]() 。然后我们挑选出另外一个随机选择的mini-batch并训练它们,等等,直到我们已经使用完所有的训练输入,我们把这个说成是完成了一个epoch的训练。在这个时候,我们就开始一个新的训练epoch。
。然后我们挑选出另外一个随机选择的mini-batch并训练它们,等等,直到我们已经使用完所有的训练输入,我们把这个说成是完成了一个epoch的训练。在这个时候,我们就开始一个新的训练epoch。
实现分类手写数字的神经网络
接下来我们以MNIST手写数字库来实现我们的神经网络。所有版权归《神经网络与深度学习》的作者,本文在翻译的基础上增加自己的理解。
关于MNIST数据集的详细信息见其官网。它被分成60,000幅训练图片和10,000幅测试图片。现在我们再将其训练图片分成2部分:50,000幅图片的集合用来训练我们的神经网络,以及一个单独的10,000幅图像为验证集。在这里我们先不使用验证数据,但是我们会发现在计算怎样设置某些神经网络的超参数是很有用的-像学习率这样的东西,等等,因为它们并不能直接地被学习算法选择出来。尽管验证数据不是原始MNIST指定的,许多人以这种方式使用MNIST,并且验证数据的使用在神经网络中是很普遍的。从现在开始,当我说"MNIST训练数据"的时候,我们是指我们的50,000图像数据集,并不是原来的60,000图像数据数据集。
除了使用MNIST数据,我们也需要一个叫Numpy的Python库,为了快速线性代数的计算。我们使用一个Network类来表示一个神经网络。下面是我们用来初始化一个Network对象的代码:
class Network():
def __init__(self,sizes):
self.num_layers=len(sizes)
self.sizes=sizes
self.biases=[np.random.randn(y,1) for y in sizes[1:]]
self.weights=[np.random.randn(y,x)
for x,y in zip(sizes[:-1],sizes[1:])]
sizes是一个列表,它包含了相关层的神经元个数。例如,如果我们想要创建一个第一层含有2个神经元,第二层含有3个神经元,最后一层含有1个神经元的Network对象,可以这样写:
net=Network([2,3,1])
Network对象中的偏置和权值都是被随机地初始化的,使用Numpy的np.random.randn函数来生成均值为0,标准差为1的高斯分布,np.random.randn(y,1)表示产生均值为0,标准差为1的y行1列的数组的高斯分布。这里权值是shape=(y,x)的数组,我们在初始化权值的时候,除了输入层,其他每一层都有一个权值向量,并且这一层的权值向量的性质由该层神经元个数和其前一层神经元个数决定,举个例子,sizes=[2,3,1]的网络结构的权值向量有2个,一个是第1层和第2层之间的连接以及第2层和第3层之间的连接。表示为w(1)和w(2),其中w(1)的形状为(3,2),w(2)的形状为(1,3)。作者写的代码很巧妙,由于分别要得到y和x的值,利用zip(sizes[:-1],sizes[1:])并行了2个列表的值。同理偏置只有1层的神经元个数决定(从第2层开始,因为第一层是输入层),对应的代码是for y in sizes[1:]。这个随机化初始给了我们的随机梯度下降算法一个开始的地方。后面我们会介绍更好地初始化权重和偏置的方式。
然后我们定义一个sigmoid函数,并使用Numpy来定义一个那个函数的一个向量化形式:
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
sigmoid_vec=np.vectorize(sigmoid) #使函数矢量化
接下来,为Network类增加一个feedforward方法,即给定网络的一个输入a,返回相应的输出。所有方法要做的就是对每一层应用等式(22):
a是第二层的神经元的激活的向量。为了得到a'我们用权值矩阵w乘以a,然后加上偏置向量。然后应用函数![]() 。
。
def feedforward(self,a):
for b,w in zip(self.biases,self.weights):
a=sigmoid_vec(np.dot(w,a)+b)
return a
下面是stochastic gradient descent的代码:
def SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None):
if test_data:
n_test=len(test_data)
n=len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches=[
training_data[k:k+mini_batch_size]
for k in xrange(0,n,mini_batch_size)
]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch,eta)
if test_data:
print "Epoch {0}:{1} / {2}".format(j,self.evaluate(test_data),n_test)
else:
print "Epoch {0} complete".format(j)
training_data是元组(x,y)的一个列表,它代表了训练输入以及相应的期望输出。变量epochs表示用来训练的epochs,以及当取样本时mini-batches的大小。eta是学习率,如果提供了可选参数test_data,那么程序将评估这个网络在每个训练的epoch之后,并且打印出局部的进展。这对于追踪过程是特别有用的,但是实质上会减慢速度。
在每个epoch中,它通过随机地shuffling训练数据,然后把它分成合适大小的mini-batches。这是一种随机抽样训练数据的简单方式。然后,对于每个mini_batch,我们应用一次梯度下降算法,这是通过代码self.update_mini_batch(mini_batch,eta)来实现的,它根据梯度下降算法的一次迭代更新权值和偏置,仅仅在mini_batch中使用训练数据。下面是update_mini_batch方法的代码:
def update_mini_batch(self,mini_batch,eta):
nabla_b=[np.zeros(b.shape) for b in self.biases] #因为我们要计算梯度的平均值
nabla_w=[np.zeros(w.shape) for w in self.weights] #梯度就是损失函数对权值和偏置分别的偏导
for x,y in mini_batch:
delta_nabla_b,delta_nabla_w=self.backprop(x,y)#利用反向传播算法求梯度(偏导),对于每一个训练输入对(x,y)
nabla_b=[nb+ dnb for nb,dnb in zip(nabla_b,delta_nabla_b)] #计算所有的梯度(对偏置b)的和
nabla_w=[nw+dnw for nw,dnw in zip(nabla_w,delta_nabla_w)] #计算所有的另外一个梯度(对权值w)的和
self.weights=[w-(eta/len(mini_batch)) * nw
for w,nw in zip(self.weights,nabla_w)] #根据更新规则更新所有的权值
self.biases=[b-(eta/len(mini_batch)) * nb
for b,nb in zip(self.biases,nabla_b)] #根据更新规则更新所有的偏置值
关键的代码在于:
delta_nabla_b,delta_nabla_w=self.backprop(x,y)
这就要引出著名的BP算法了,它是一种快速计算损失函数的梯度的一种方法。update_mini_batch是通过为mini_batch里的每个训练样本计算这些梯度,然后更新self.weights以及self.biases。这里关于BP算法暂时先不探讨,只要知道self.backprop的代码返回训练样本x关联的损失的相应的梯度值。
>>>import network
>>>net=network.Network([784,30,10])
最终,我们将使用随机梯度下降来学习MNIST的training_data 30 epochs,其中mini-batch的大小为10,以及一个学习率![]() =3.0。
=3.0。
>>>net.SGD(training_data,30,10,3.0,test_data=test_data)
详细代码在这里。
参考文献《neural networks and deep learing》
转载 http://www.gumpcs.com/index.php/archives/799