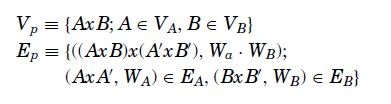异构计算-2-根据程序的属性分类

2，方法

我们的分类方法（CENTRIFUGE）分成三部：建立程序的representation，分组，评估。第一步包括收集function的静态和动态属性以得到程序的近似描述。第二步包括两个步骤：比较，和分组。比较，包括测试不同function的近似描述来判断他们的相似度。然后根据相似度的信息将这些function分成相似的几个集合。第二步最后是对每个分组的function进行研究。第三步，根据每个分组的面积来分析这种分组方法行还是不行。本章描述这些步骤的细节并大概介绍一下具体的处理过程。

 

2.1属性

确定代码行为的首要任务就是找到变现function行为的静态/动态特征。好的特征可以很好的采集到那些影响性能的属性。本文中，我们包含传统的静态/动态特征，比如，static instruction mix,

static control/data flow graphs ，dynamic data flow graphs. 此外我们还有两个新的特征:带局部信息的 dynamic dataflow graphs 和用现有的优化方法，function的性能表现怎么样。这些属性如下：

（1）       Static Instruction Mix。这个属性可以作为优化后function如何反应的一个很好的指标。比如，根据这个分类可能会产生计算型function，或者数据移动型function，这样对不同分类的优化就有不同的效果。我们怎么计算静态属性呢，就是我们不加任何优化选项对程序进行编译，然后把所有的指令分成以下几类：controltransfer, arithmetic, logical, 和memory.这样，每个类别中的一小部分指令集就是一个向量，这个向量就代表代码库中的每个function。

（2）       Static CDFG。这个东西经成用来进行编译器分析。这些图表可以表现一个function的并行度。因此可以很好的表示function的行为。在一般的编译器分析中，在流图（flow graphs）中，我们用basic blocks作为顶点。我们现在的流图中，我们用basic block instruction mixes作为顶点，以依赖类型作为边（control, must pointer, may pointer, register）。这些依赖关系是用LLVM编译器产生的。

（3）       DynamicDFG。他包含静态存储器依赖信息。这个依赖信息是通过算法分析来计算的。情况很糟的话，充足的保守分析会产生全部相连的依赖图表。由于这只有一个包含顶点数目完全图表，这个简单的分析会减少function的信息量。另一方面，关于function的信息，动态数据流图比Static CDFG更详细，因为他们只反映了实测依赖边，而不是潜在的依赖边。此外，我们可以给这些图表加一些注释，比如其他的动态信息。本文中，我们用依赖观测频率（基本快的执行次数）来增加依赖边权重到我们的DynamicDFG。为了给这些图表的顶点做注释，我们计算基本快的依赖链长度（在一个基本块内部最长的生产-x消费链的长度），整型指令的数量，浮点指令的数量，存储器加载的数量。动态特征（比如，执行次数）也会用到，这个会增加分析的灵敏度。

（4）       Dynamic DFG with Load Distance。大家都知道，数据局部性是影响性能的关键因素，除此之外，还有并行性。CDFG andDynamic DFG可以很好的采集并行性的约束条件，但不能采集数据局部性。为了采集数据局部性，我们测量动态指令的数目，因为每个加载的地址就是程序中最近访问的地址（用PIN，不带优化）。这跟重用距离相似，不同的是，我们计算指令数目，而不是内存访问数。例如，一个被调函数访问地址X，这个地址刚被调用函数写过，就会产生很短的加载距离。但是，如果，地址X,最近一次是被初始化程序写的，并且再也没有读过，那么就会产生很长的加载距离（load distance），这样，在局部在处理器高速缓存中的概率就很小。然后，我们计算一个function中所有加载距离的平均偏差的对数，和标准偏差的对数，然后这两个数作为重用的标志。

（5）       Function Optimization Reactions（函数优化反应）。作为上面属性的补充，我们还用应经存在的优化选项来进行分类。我们感觉，对相似的函数进行优化的话，那么他们的反应也应该相似。因此，利用这些优化反应，可能会给我们一个函数属性的简介指示。我们用对一个函数用不同的优化选项，测量这个函数的执行时间，计算这个函数的优化反应（公式7），来建立这个模型。根据优化反应对函数进行分类。

2.2 比较方法

现在我们有了进行分类的特征，下一步就是确定如何比较这些特征。我们通过定义距离函数来弄：用向量来代表特征，我们用两个向量间的欧几里得距离来测量他们的相似度。在我们最初的试验中发现，欧几里得距离比曼哈顿距离要好。对于两个向量A和B，长度为n，那么他们的欧几里得距离就是：

比较绘画属性更复杂，这个以后下一步会说。

         传统的图形比较算法，比如isomorphism and subgraph isomorphism，的结果是匹配或者不匹配，只有两种可能，这对比较两个函数的相似度没有意义。与此不同，我们用approximategraph comparison技术来计算两个图形的距离。确定这个距离需要两步： mapping andscoring（映射和得分）。映射这一步，我们给来自两个输入图形的节点进行配对。就是，对于图A的每个顶点，我们在图B中找到和这个顶点最相似的顶点，并且从局部性（localinformation）这方面来说也是相似的，并且邻居信息（neighborhoodinformation）也是相似的。得分这一步，用这个映射来计算顶点和图形结构相似度。根据我们的图形性特征，这个过程适合找相似的基本块，然后，利用边界信息（edgeinformation）来判断两个函数的相似度。

映射。映射已经在别人的论文里提到过了（SimilarityFlooding）。我们的方法跟他的类似，但是我们稍微修改了一下，就是在不同阶段的值的正常化方式。我们的基本思想是构建一个新的图表，这个图表包括向量的虽有配对组合，还有就是包括两个原始图表的边界分开的边界。我们给这个图表中的每个向量分配一个近似值，然后沿着边界迭代的扩展这些值。在收敛的情况下，每个值就表示一对向量的相似性，也就代表基本块的函数的相似性，其实也就是图表的结构的相似性。我们可以用这些值来确定最好的映射。举个例子，图3是这个图展示了这些细节。

正式一点，我们给两个待比较的函数图表建立一个张量积图表。对于图表A（Va,Ea）和B（Vb,Eb）,他们的张量积（Vp,Ep）表示为：

最后的图表（product graph）包含所有可能的映射，所以最后的映射就是这个图表的一个子集。

下一步，我们定义一个最初的product graph的向量相似性的函数，D（v）.在我们的方案里，每个product graph中的顶点代表一对基本块，所以我们用两个基本块指令混合的曼哈顿距离（Manhattandistance）。如下：

第三步，就是沿着图表的边来扩展相似性的得分。这是一个迭代计算，每一步用i代表，对V，我们计算每个顶点(j)的值（Mij），通过相邻顶点的一个集合和边权重，Ej,和Wj：

这一步有一个隐含的条件，就是如果一个节点匹配很好，那么他的相邻节点也会匹配很好，也就是说他的得分就会增加。

输出格式是这样的，是一个顶点-顶点对得分的矩阵，这个反映了基本块和结构的相似性。因此，确定最好匹配，就变成了选择一个最好的相似的对儿。这是一个赋值问题，我们用著名的匈牙利算法（HungarianAlgorithm）来解决。

 

得分。一旦建立了最优映射，我们就可以比较两个输入图表，然后给比较图表打分。有很多打分方法。有人可能会用映射阶段的那个方法。但是这个方法会受匹配不好的图表的影响。

我们有重新设计了一个算法，就是用曼哈顿距离和结构性不匹配（structuralmismatch）的混合。在V中，对于每个比较的顶点I,基本块指令混合的曼哈顿距离(Di),一般共享边地数目（Si）,未共享的边的数目（Ei）。对不相似的顶点，我们按照如下公式计算得分：

 

2.3 分类方法

分类方法有很多，如agglomerativeclustering, k-means, or SOM。本文用跟agglomerative类似的方法：

(1) Instruction Mix. Euclidean distance

(2) Static CDFG. Similarityflooding-based graph distance defined in Section 2.2 using

unity edge weights.

(3) Dynamic DFG. Similarityflooding-based graph distance defined in Section 2.2.

(4) Locality Annotated Dynamic DFG.

（5）Optimization Reaction Metric: