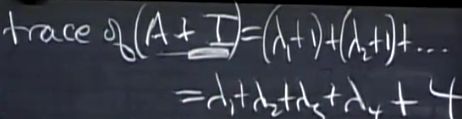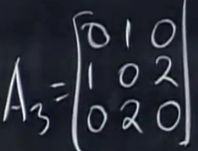线性代数导论25——第二阶段总结
本文是Gilbert Strang的线性代数导论课程笔记。课程地址: http://v.163.com/special/opencourse/daishu.html
第二十五课时:第二阶段总结
本讲是对前阶段的复习课。主要内容有正交性Q
TQ=I;计算到线和子空间的投影,用来解决Ax=b的问题;格拉姆-施密特正交化将无关的向量投影到另一向量,将获得的向量投影从向量中减去,新得到向量和之前的正交,将基变为标准正交基;行列式;特征值和特征向量。发现教授的复习课时很重要的,他的例子能让知识连贯起来,触类旁通。
题1:三维向量空间中,有a(2 1 2),要找到投影矩阵P,使得任意向量投影到a的投影矩阵为P,P的特征值和特征向量是多少?求解差分方程uk+1=Puk,u0=(9 9 0)
得到投影矩阵P如上图,特征值有三个0,0,1,
特征值为1的特征向量是哪个?哪个向量经过投影矩阵后不变,只有向量a是这样的了,所以可以求出特征向量。(还记得特征值和特征向量那一讲吗?特意讲了投影矩阵,它的特征值就是0和1)
那么u1=Pu0,表示将向量u0投影到线a上,因为u1就在a所在的直线上,那么Pu1=u1,因此可得uk的值就等于Pu0=(6 3 6)。(或者可以这样解释:
投影矩阵Pk=P)。
假设差分方程中,矩阵并不是投影矩阵P,那么该如何求解呢?此时需要求特征值和特征向量按部就班来做。
从上式看,如果A是投影矩阵,那么λ1=λ2=0,前两项为0,后一项为c3x3。
题2:将给定点拟合到一条过原点的直线y=Dt。求最优的D。
复习投影矩阵。将向量b(4 5 8)投影到了A的列空间,可得到:
题3:有两个向量a1=(1 2 3), a2=(1 1 1),找到这两个向量所在平面的一组正交基。(如果找到一组,旋转一下又可以找到另外一组,格拉姆-施密特方法可以从一个向量做起)
题4:4×4的矩阵A,有四个特征值λ1,λ2,λ3,λ4。
1)
什么样的特征值可满足矩阵可逆?特征值都不等于0,零意味着零空间里有非零向量。
2)
A逆的行列式为多少?A的逆的特征值相乘就是它的行列式,A的逆的特征值等于A的特征值的倒数。
3)
A+I的迹是多少?把A+I的特征值相加就等于它的迹了。A+I的特征值等于A的特征值加1,
题5:已知A4,求Dn=det(An)。使用代数余子式。Dn到底是收敛还是越来越大还是周期性的改变。
找出递归式,初始值D1=1,D2=0
求Dn,可通过求特征值特征向量来求得。特征值求得是共轭复数。
λ的六次方等于1,Dn是周期性的变化。矩阵的6次方的特征值为1.
题6:如下矩阵
1)A4投影到A3的列空间的投影矩阵,很容易想到的方法
:P=A(ATA)-1AT,可得投影矩阵。
2)求A3的特征值和特征向量。
3)
求A4的投影矩阵(即投影到A4列空间的投影矩阵)。因为A4的行列式不等于0,所以A4可逆,列空间为整个空间,所以投影矩阵为I.