一起talk C栗子吧(第五十四回:C语言实例--图的最短路径二)
各位看官们,大家好,上一回中咱们说的是最短路径的例子,这一回咱们继续说:图的最短路径,闲话休
提,言归正转。让我们一起talk C栗子吧!
看官们,我们在上一回中介绍了最短路径相关的概念,这一回中我们介绍如何使用迪杰斯特拉(Dijkstra)
算法去求顶点之间的最短路径。
迪杰斯特拉算法的基本思路:假设需要计算起点A和终点B之间的最短路径。首先计算出离起点距离近的顶
点与起点之间的最短距离,然后再计算出离起点距离远的顶点与起点之间的最短距离,如此反复,一直到
达终点为止。这里的远近关系可以这样去理解,如果两个顶点之间有直接的边,那么这两个顶点的距离就
比较近,反之,这两个顶点距离就比较远。
迪杰斯特拉算法的实现步骤:
- 1.选取图中任意一个顶点当作起点,对起点进行标记,表示它已经被访问过;
- 2.从图的邻接矩阵中读取与起点相连边的权值,并且存放到一个数组中;
- 3.在数组中找到权值最小的边,把该权值保存起来当作最短路径;
- 4.把步骤2中“权值最小的边”的另外一个顶点当作新的起点,对新起点进行标记,表示它已经被访问过;
- 5.查找是否可以通过新起点找到最短路径,如果有最短路径,那么更新存放最短路径的数组;
- 6.重复步骤3到步骤5,直到图中所有顶点都被查找完为止;
看官们,正文中就不写代码了,详细的代码放到了我的资源中,大家可以点击这里下载使用。关于该程序
我做以下的说明,方便大家理解:
- 1.程序中使用了一个数组来标记某个顶点是否被访问过,这样可以避免重复访问同一个顶点,从而避免计算出错误的最短路径。
- 2.程序中计算出了第一个顶点到其它顶点的的最短路径,如果想计算其它顶点之间的最短路径,只需要在程序中修改起点就能实现该目标。
- 3.程序中计算最短路径时,各个顶点的权值都是正数,如果有某个权值是负数,那么该算法就无能为力了。因此,在使用该算法时需要注意这点。
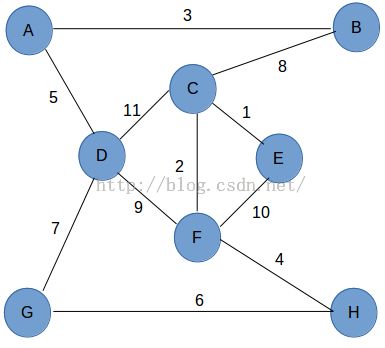
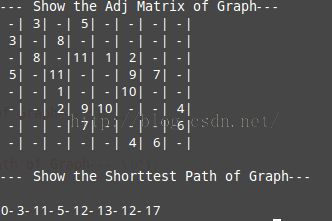
下面是程序的运行结果以及程序中使用的图。从程序运行结果中可以看到,顶点A到其它顶点的距离为A->B:3,
A->C:11依此类推,A->H:17.大家可以通过对比的方式查看程序运行结果和截图,这样可以更好地理解程序的
原理。
(程序中使用的图) (程序的运行结果)
各位看官,关于最短路径的例子咱们就说到这里。欲知后面还有什么例子,且听下回分解。