高斯混合模型（GMM）实现和可视化

作者：金良（[email protected]） csdn博客： http://blog.csdn.net/u012176591

需要整理后的代码文件和数据请移步 http://download.csdn.net/detail/u012176591/8748673

1.高斯分布公式及图像示例

定义在D-维连续空间的高斯分布概率密度的表达式
N(x|μ,Σ)=1(2π)D/21|Σ|1/2exp{−12(x−μ)TΣ−1(x−μ)}

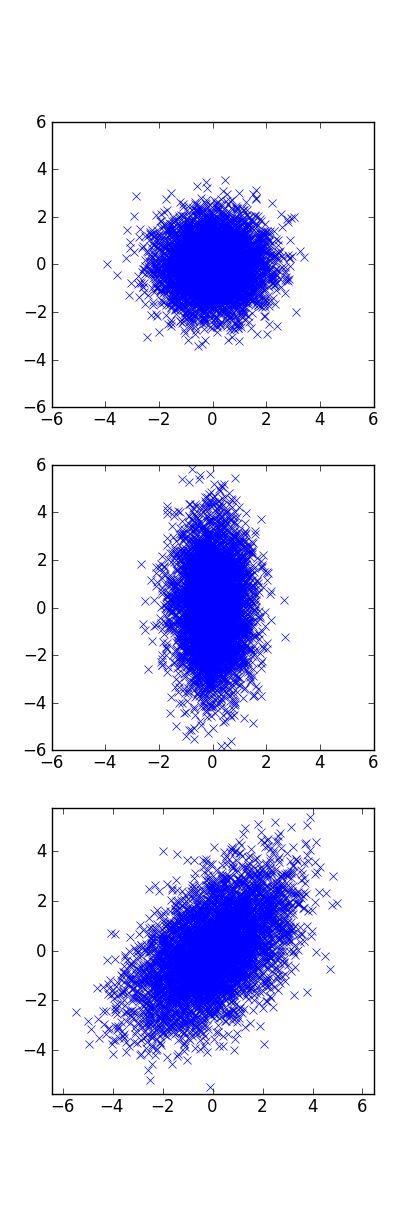
其等高线所形成的形状与协方差矩阵 Σ 密切相关，如下所示，后面的代码中有各个图像的对应的高斯分布的参数。

2. 高斯分布概率密度热力图

代码如下：

fig,axes = plt.subplots(nrows=3,ncols=1,figsize=(4,12))

# 标准圆形
mean = [0,0]
cov = [[1,0],
       [0,1]] 
x,y = np.random.multivariate_normal(mean,cov,5000).T
axes[0].plot(x,y,'x')
axes[0].set_xlim(-6,6) 
axes[0].set_ylim(-6,6) 

# 椭圆，椭圆的轴向与坐标平行
mean = [0,0]
cov = [[0.5,0],
       [0,3]] 
x,y = np.random.multivariate_normal(mean,cov,5000).T
axes[1].plot(x,y,'x')
axes[1].set_xlim(-6,6) 
axes[1].set_ylim(-6,6) 

# 椭圆，但是椭圆的轴与坐标轴不一定平行
mean = [0,0]
cov = [[1,2.3],
       [2.3,1.4]] 
x,y = np.random.multivariate_normal(mean,cov,5000).T
axes[2].plot(x,y,'x'); plt.axis('equal')
axes[2].set_xlim(-6,6) 
axes[2].set_ylim(-6,6) 

我们在下面的高斯混合模型中采用用第三种协方差矩阵，即概率密度的等高线是椭圆，且轴向不一定与坐标轴平行。

下图是高斯密度函数的热图：

以下是作图代码

# 自定义的高维高斯分布概率密度函数
def gaussian(x,mean,cov):    
    dim = np.shape(cov)[0] #维度
    covdet = np.linalg.det(cov+np.eye(dim)*0.01) #协方差矩阵的秩
    covinv = np.linalg.inv(cov+np.eye(dim)*0.01) #协方差矩阵的逆
    xdiff = x - mean
    #概率密度
    prob = 1.0/np.power(2*np.pi,1.0*2/2)/np.sqrt(np.abs(covdet))*np.exp(-1.0/2*np.dot(np.dot(xdiff,covinv),xdiff))

    return prob


#作二维高斯概率密度函数的热力图
mean = [0,0]
cov = [[1,2.3],
       [2.3,1.4]] 
x,y = np.random.multivariate_normal(mean,cov,5000).T
cov = np.cov(x,y) #由真实数据计算得到的协方差矩阵，而不是自己任意设定
n=200
x = np.linspace(-6,6,n)
y = np.linspace(-6,6,n)
xx,yy = np.meshgrid(x, y)
zz = np.zeros((n,n))
for i in range(n):
    for j in range(n):
        zz[i][j] = gaussian(np.array([xx[i][j],yy[i][j]]),mean,cov)

gci = plt.imshow(zz,origin='lower') # 选项origin='lower' 防止tuixan图像颠倒
plt.xticks([5,100,195],[-5,0,5])
plt.yticks([5,100,195],[-5,0,5])
plt.title(u'高斯函数的热力图',{'fontname':'STFangsong','fontsize':18})

３.高斯混合模型实现代码：

下面是几个功能函数，在主函数中被调用

# 计算概率密度，
# 参数皆为array类型，过程中参数不变
def gaussian(x,mean,cov):

    dim = np.shape(cov)[0] #维度
    #之所以加入单位矩阵是为了防止行列式为0的情况
    covdet = np.linalg.det(cov+np.eye(dim)*0.01) #协方差矩阵的行列式
    covinv = np.linalg.inv(cov+np.eye(dim)*0.01) #协方差矩阵的逆
    xdiff = x - mean
    #概率密度
    prob = 1.0/np.power(2*np.pi,1.0*dim/2)/np.sqrt(np.abs(covdet))*np.exp(-1.0/2*np.dot(np.dot(xdiff,covinv),xdiff))
    return prob


#获取初始协方差矩阵
def getconvs(data,K):
    convs = [0]*K
    for i in range(K):
        # 初始的协方差矩阵源自于原始数据的协方差矩阵，且每个簇的初始协方差矩阵相同
        convs[i] = np.cov(data.T)  
    return convs


def isdistinct(means,criter=0.03): #检测初始中心点是否靠得过近
    K = len(means)
    for i in range(K):
        for j in range(i+1,K):
            if criter > np.linalg.norm(means[i]-means[j]):
                return 0       
    return True
#获取初始聚簇中心
def getmeans(data,K,criter):
    means = [0]*K
    dim  = np.shape(data)[1]
    minmax = [] #各个维度的极大极小值
    for i in range(dim):
        minmax.append(np.array([min(data[:,i]),max(data[:,i])]))

    while True:
        #生成初始点的坐标
        for i in range(K):
            means[i] = []
            for j in range(dim):
                means[i].append(np.random.random()*(minmax[j][1]-minmax[j][0])+minmax[j][0])  
            means[i] = np.array(means[i])

        if isdistinct(means,criter):
            break  
    return means

# k-means算法的实现函数。
#用K-means算法输出的聚类中心，作为高斯混合模型的输入
def kmeans(data,K):
    N = np.shape(data)[0]#样本数目
    dim = np.shape(data)[1] #维度

    means = getmeans(data,K,criter=15)
    means_old = [np.zeros(dim) for k in range(K)]


    while np.sum([np.linalg.norm(means_old[k]-means[k]) for k in range(K)]) > 0.01:

        means_old = cp.deepcopy(means)

        numlog = [0]*K
        sumlog = [np.zeros(dim) for k in range(K)]
        for n in range(N):
            distlog = [np.linalg.norm(data[n]-means[k]) for k in range(K)]
            toK = distlog.index(np.min(distlog))

            numlog[toK] += 1
            sumlog[toK] += data[n]

        for k in range(K):
            means[k] = 1.0/numlog[k]*sumlog[k]
    return means

#对程序结果进行可视化，注意这里的K只能取2，否则该函数运行出错
def visualresult(data,gammas,K):
    N = np.shape(data)[0]#样本数目
    dim = np.shape(data)[1] #维度

    minmax = [] #各个维度的极大极小值
    xy = []
    n=200
    for i in range(dim):
        delta = 0.05*(np.max(data[:,i])-np.min(data[:,i]))
        xy.append(np.linspace(np.min(data[:,i])-delta,np.max(data[:,i])+delta,n))
    xx,yy = np.meshgrid(xy[0], xy[1])
    zz = np.zeros((n,n))
    for i in range(n):
        for j in range(n):
            zz[i][j] = np.sum(gaussian(np.array([xx[i][j],yy[i][j]]),means[k],convs[k]) for k in range(K))
    gci = plt.imshow(zz,origin='lower',alpha = 0.8) # 选项origin='lower' 防止tuixan图像颠倒
    plt.xticks([0,len(xy[0])-1],[xy[0][0],xy[0][-1]])
    plt.yticks([0,len(xy[1])-1],[xy[1][0],xy[1][-1]])

    for i in range(N):
        if gammas[i][0] >0.5:
            plt.plot((data[i][0]-np.min(data[:,0]))/(xy[0][1]-xy[0][0]),(data[i][1]-np.min(data[:,1]))/(xy[1][1]-xy[1][0]),'r.')
        else:
            plt.plot((data[i][0]-np.min(data[:,0]))/(xy[0][1]-xy[0][0]),(data[i][1]-np.min(data[:,1]))/(xy[1][1]-xy[1][0]),'k.')

    deltax = xy[0][1]-xy[0][0]
    deltay = xy[1][1]-xy[1][0]

    plt.plot((means[0][0]-xy[0][0])/deltax,(means[0][1]-xy[1][0])/deltay,'*r',markersize=15)
    plt.plot((means[1][0]-xy[0][0])/deltax,(means[1][1]-xy[1][0])/deltay,'*k',markersize=15)

    plt.title(u'高斯混合模型图',{'fontname':'STFangsong','fontsize':18})

高斯混合模型的主函数

N = np.shape(data)[0]#样本数目
dim = np.shape(data)[1] #维度
K = 2 # 聚簇的个数

means = kmeans(data,K)

convs = getconvs(data,K)

pis = [1.0/K]*K
gammas = [np.zeros(K) for i in range(N)] #*N 注意不能用 *N，否则N个array只指向一个地址

loglikelyhood = 0
oldloglikelyhood = 1

while np.abs(loglikelyhood - oldloglikelyhood)> 0.0001:
    oldloglikelyhood = loglikelyhood


    # E_step
    for n in range(N):
        respons = [pis[k]*gaussian(data[n],means[k],convs[k]) for k in range(K)]

        sumrespons = np.sum(respons)
        for k in range(K):
            gammas[n][k] = respons[k]/sumrespons

    # M_step
    for k in range(K):
        nk = np.sum([gammas[n][k] for n in range(N)])
        means[k] = 1.0/nk * np.sum([gammas[n][k]*data[n] for n in range(N)],axis=0)

        xdiffs = data - means[k]
        convs[k] = 1.0/nk * np.sum([gammas[n][k]*xdiffs[n].reshape(dim,1)*xdiffs[n] for n in range(N)],axis=0)
        pis[k] = 1.0*nk/N

    # 计算似然函数值
    loglikelyhood =np.sum( [np.log(np.sum([pis[k]*gaussian(data[n],means[k],convs[k]) for k in range(K)])) for n in range(N) ])
    #print means
    #print loglikelyhood
    #print '=='*10

visualresult(data,gammas,K)

4.高斯混合模型聚簇效果图

5.参考文献：

• K-means聚类和EM思想
  http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html
• （EM算法）The EM Algorithm
  http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
• 从决策树学习谈到贝叶斯分类算法、EM、HMM
  http://blog.csdn.net/v_july_v/article/details/7577684
• EM算法学习(Expectation Maximization Algorithm)
  http://www.vjianke.com/XUHV3.clip
• EM算法——理论与应用
  http://blog.sina.com.cn/s/blog_a8fead9b01014p6k.html
• EM算法 一个简单的例子
  http://blog.sina.com.cn/s/blog_a7da5cda010158b3.html
• 高斯混合模型（GMM）
  http://www.cnblogs.com/mindpuzzle/archive/2013/04/24/3036447.html
• 高斯混合模型
  http://www.cnblogs.com/zhangchaoyang/articles/2624882.html
• CS229 Lecture notes,Andrew Ng讲义
  http://cs229.stanford.edu/notes/cs229-notes7b.pdf
• https://github.com/lzhang10/maxent/blob/master/doc/manual.pdf
• http://nlp.stanford.edu/software/classifier.shtml
• https://github.com/juandavm/em4gmm
  用最大期望算法求解高斯混合模型，dat文件夹里的压缩文件是数据
• http://insideourminds.net/python-unsupervised-learning-using-em-algorithm-implementation/
  Python实现的期望最大化算法，数据是鸢尾花数据