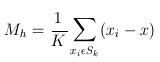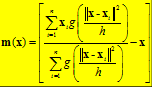机器学习（十）Mean Shift 聚类算法

Mean Shift 聚类算法

原文地址：http://blog.csdn.net/hjimce/article/details/45718593 

作者：hjimce

一、mean shift 算法理论

Mean shift 算法是基于核密度估计的爬山算法，可用于聚类、图像分割、跟踪等，因为最近搞一个项目，涉及到这个算法的图像聚类实现，因此这里做下笔记。

(1)均值漂移的基本形式

给定d维空间的n个数据点集X，那么对于空间中的任意点x的mean shift向量基本形式可以表示为：

这个向量就是漂移向量，其中Sk表示的是数据集的点到x的距离小于球半径h的数据点。也就是：

而漂移的过程，说的简单一点，就是通过计算得漂移向量，然后把球圆心x的位置更新一下，更新公式为：

使得圆心的位置一直处于力的平衡位置。

 

总结为一句话就是：求解一个向量，使得圆心一直往数据集密度最大的方向移动。说的再简单一点，就是每次迭代的时候，都是找到圆里面点的平均位置作为新的圆心位置。

(2)加入核函数的漂移向量

这个说的简单一点就是加入一个高斯权重，最后的漂移向量计算公式为：

因此每次更新的圆心坐标为：

不过我觉得如果用高斯核函数，把这个算法称为均值漂移有点不合理，既然叫均值漂移，那么均值应该指的是权重相等，也就是(1)中的公式才能称之为真正的均值漂移。

我的简单理解mean shift算法是：物理学上力的合成与物体的运动。每次迭代通过求取力的合成向量，然后让圆心沿着力的合成方向，移动到新的平衡位置。

二、mean shift 聚类流程：

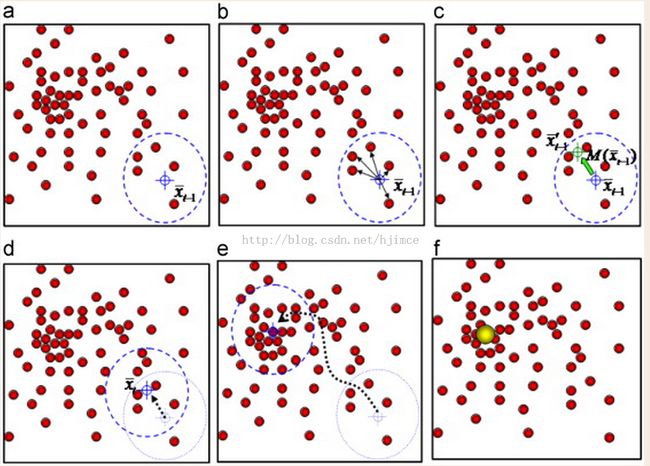
假设在一个多维空间中有很多数据点需要进行聚类，Mean Shift的过程如下：

1、在未被标记的数据点中随机选择一个点作为中心center；

2、找出离center距离在bandwidth之内的所有点，记做集合M，认为这些点属于簇c。同时，把这些求内点属于这个类的概率加1，这个参数将用于最后步骤的分类

3、以center为中心点，计算从center开始到集合M中每个元素的向量，将这些向量相加，得到向量shift。

4、center = center+shift。即center沿着shift的方向移动，移动距离是||shift||。

5、重复步骤2、3、4，直到shift的大小很小（就是迭代到收敛），记住此时的center。注意，这个迭代过程中遇到的点都应该归类到簇c。

6、如果收敛时当前簇c的center与其它已经存在的簇c2中心的距离小于阈值，那么把c2和c合并。否则，把c作为新的聚类，增加1类。

6、重复1、2、3、4、5直到所有的点都被标记访问。

7、分类：根据每个类，对每个点的访问频率，取访问频率最大的那个类，作为当前点集的所属类。

简单的说，mean shift就是沿着密度上升的方向寻找同属一个簇的数据点。

三、mean shift 聚类实现

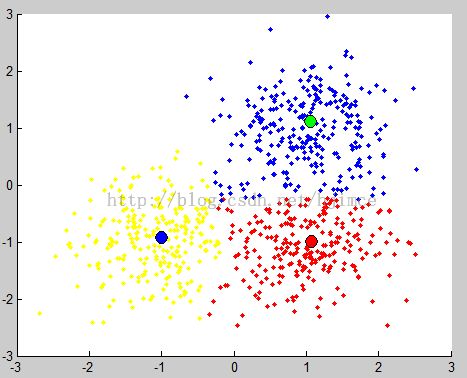
Mean shift 算法不需要指定聚类个数，贴一下用matlab实现的聚类结果：

clc close all; clear profile on %生成随机数据点集 nPtsPerClust = 250; nClust = 3; totalNumPts = nPtsPerClust*nClust; m(:,1) = [1 1]'; m(:,2) = [-1 -1]'; m(:,3) = [1 -1]'; var = .6; bandwidth = .75; clustMed = []; x = var*randn(2,nPtsPerClust*nClust); for i = 1:nClust x(:,1+(i-1)*nPtsPerClust:(i)*nPtsPerClust) = x(:,1+(i-1)*nPtsPerClust:(i)*nPtsPerClust) + repmat(m(:,i),1,nPtsPerClust); end data=x'; % plot(data(:,1),data(:,2),'.') %mean shift 算法 [m,n]=size(data); index=1:m; radius=0.75; stopthresh=1e-3*radius; visitflag=zeros(m,1);%标记是否被访问 count=[]; clustern=0; clustercenter=[]; hold on; while length(index)>0 cn=ceil((length(index)-1e-6)*rand);%随机选择一个未被标记的点，作为圆心，进行均值漂移迭代 center=data(index(cn),:); this_class=zeros(m,1);%统计漂移过程中，每个点的访问频率 %步骤2、3、4、5 while 1 %计算球半径内的点集 dis=sum((repmat(center,m,1)-data).^2,2); radius2=radius*radius; innerS=find(dis<radius*radius); visitflag(innerS)=1;%在均值漂移过程中，记录已经被访问过得点 this_class(innerS)=this_class(innerS)+1; %根据漂移公式，计算新的圆心位置 newcenter=zeros(1,2); % newcenter= mean(data(innerS,:),1); sumweight=0; for i=1:length(innerS) w=exp(dis(innerS(i))/(radius*radius)); sumweight=w+sumweight; newcenter=newcenter+w*data(innerS(i),:); end newcenter=newcenter./sumweight; if norm(newcenter-center) <stopthresh%计算漂移距离，如果漂移距离小于阈值，那么停止漂移 break; end center=newcenter; plot(center(1),center(2),'*y'); end %步骤6 判断是否需要合并，如果不需要则增加聚类个数1个 mergewith=0; for i=1:clustern betw=norm(center-clustercenter(i,:)); if betw<radius/2 mergewith=i; break; end end if mergewith==0 %不需要合并 clustern=clustern+1; clustercenter(clustern,:)=center; count(:,clustern)=this_class; else %合并 clustercenter(mergewith,:)=0.5*(clustercenter(mergewith,:)+center); count(:,mergewith)=count(:,mergewith)+this_class; end %重新统计未被访问过的点 index=find(visitflag==0); end%结束所有数据点访问 %绘制分类结果 for i=1:m [value index]=max(count(i,:)); Idx(i)=index; end figure(2); hold on; for i=1:m if Idx(i)==1; plot(data(i,1),data(i,2),'.y'); elseif Idx(i)==2; plot(data(i,1),data(i,2),'.b'); elseif Idx(i)==3; plot(data(i,1),data(i,2),'.r'); elseif Idx(i)==4; plot(data(i,1),data(i,2),'.k'); elseif Idx(i)==5; plot(data(i,1),data(i,2),'.g'); end end cVec = 'bgrcmykbgrcmykbgrcmykbgrcmyk'; for k = 1:clustern plot(clustercenter(k,1),clustercenter(k,2),'o','MarkerEdgeColor','k','MarkerFaceColor',cVec(k), 'MarkerSize',10) end

在图像分割、图像跟踪，需要加入核函数。

聚类结果                                                                                           圆心漂移轨迹

*********作者：hjimce     联系qq：1393852684   更多资源请关注我的博客：http://blog.csdn.net/hjimce                原创文章，版权所有，转载请保留本行信息。*****************