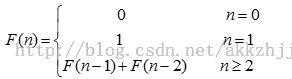常用算法之分治法与动态规划法
之所以把这两种算法放到一起,是因为它们都是用来求最优解的问题,与贪心算法是不同的。但是这两种算法又有一些区别,下面来做解释:
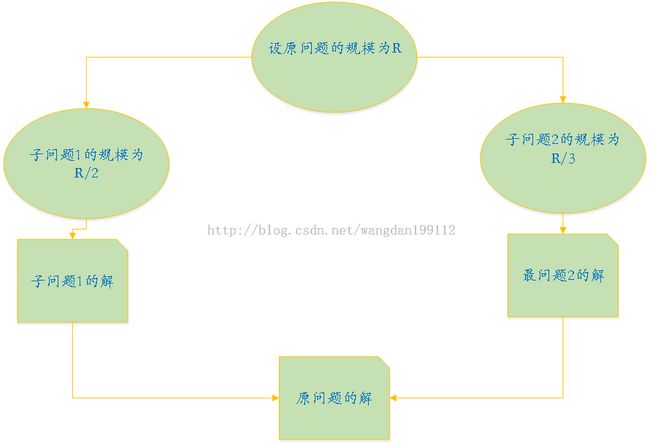
分治,即分而治之,把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
上图用一个例子来解释如下:
当n>1时,想求得T(n),必须知道T(n-1),以此类推,所以要想求得T(n)就必须将T(n)分解,从最小的子问题开始计算,最终求得T(n),这个过程就是一个递归。分治与递归像一对孪生兄弟,经常在分治中用到递归。
使用场合:
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解;
4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加;
第二条特征是应用分治法的前提它也是大多数问题可以满足的,此特征反映了递归思想的应用;、
第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。
第四条特征涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
应用框架:
/*分治法——归并排序
* 二路归并排序的分治策略是:
(1)划分:将待排序序列r1, r2, …, rn划分为两个长度相等的子序列r1, …, rn/2和rn/2+1, …, rn;
(2)求解子问题:分别对这两个子序列进行排序,得到两个有序子序列;
(3)合并:将这两个有序子序列合并成一个有序序列。
*/
public class MergeSort {
/**
* @param args
*/
public static void main(String[] args) {
int a[] = { 21, 34, 56, 43, 99, 37, 78, 10 };// 这里对8个元素进行排序
int low = 0, high = 7;// 初始化low和high的值,即数组的起始和终止的坐标
// 辅助数组b,作为临时数组
int b[] = new int[a.length];
//输出排序前的数组
System.out.print("排序前:");
for (int i = 0; i <= high; i++) {
System.out.print(a[i] + " ");
}
// 归并排序
mergerSort(a, low, high, b);
//输出排序后的数组
System.out.print("排序后:");
for (int i = 0; i <= high; i++) {
System.out.print(a[i] + " ");
}
}
/**
* 分治和归并
*
* @param a
* @param low
* @param high
* @param b
*/
public static void mergerSort(int a[], int low, int high, int b[]) {
int mid = 0;
if (low < high) {
mid = (high + low) / 2;// 分治位置,即将数组拆分的位置
mergerSort(a, low, mid, b);
mergerSort(a, mid + 1, high, b);
merger(a, low, mid, high, b);// 归并
}
}
/**
* 合并两个有序子序列
*
* @param a
* @param low
* @param mid
* @param high
* @param b
* 辅助数组
*/
public static void merger(int[] a, int low, int mid, int high, int b[]) {
int i = low;
int j = mid + 1;
int p = 0;
// 合并两个有序数组 子序列1 a[low..mid] 子序列2 a[mid+1..high]
while (i <= mid && j <= high) {
b[p++] = (a[i] <= a[j]) ? a[i++] : a[j++];
}
// 如果子序列1没有合并完则直接复制到复制数组中去
while (i <= mid) {
b[p++] = a[i++];
}
// 如果子序列2没有合并完则直接复制到复制数组中去
while (j <= high) {
b[p++] = a[j++];
}
// 把辅助数组的元素复制到原来的数组中去
for (p = 0, i = low; i <= high; i++, p++) {
a[i] = b[p];
}
}
}
而动态规划法与分治法有什么区别呢?由于文章篇幅过长,请看系列博客: 常用算法之动态规划法