字典树
1.字典树在串的快速检索中的应用。
给出N个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。在这道题中,我们可以用字典树,先把熟词建一棵树,然后读入文章进行比较,这种方法效率是比较高的。
2. 字典树在“串”排序方面的应用
给定N个互不相同的仅由一个单词构成的英文名,让你将他们按字典序从小到大输出用字典树进行排序,采用数组的方式创建字典树,这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。
3. 字典树在最长公共前缀问题的应用
对所有串建立字典树,对于两个串的最长公共前缀的长度即他们所在的结点的公共祖先个数,于是,问题就转化为最近公共祖先问题。
使用字典树的好处:
1.利用字符串的公共前缀来节约存储空间。
2.最大限度地减少无谓的字符串比较,查询效率比较高。例如:若要查找的字符长度是5,而总共有单词的数目是26^5=11881376,利用trie树,利用5次比较可以从11881376个可能的关键字中检索出指定的关键字,而利用二叉查找树时间复杂度是O( log2n ),所以至少要进行log211881376=23.5次比较。可以看出来利用字典树进行查找速度是比较快的。
既然有这么多的好处和用处,那么字典树到底是一个什么东西呢,先来看一张图,这就是一个最简单的字典树 。 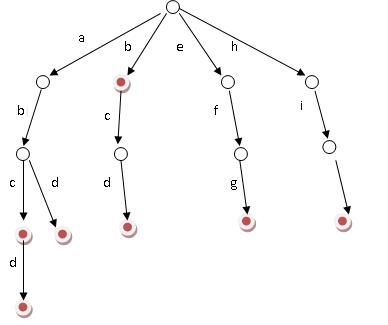 字典树给出abcd,abd,bcd,efg,hi等这样的几个字符串,我们就建立这样的一棵树,最上面是root节点,它是一个空的节点,在root节点下面有很多节点,如果我们是只是小写的字符串的话,我们就可以设置26个节点,但是怎样把他们连起来呢,看到箭头我们就能想到用链表了,既上面的每一个字母都是一个节点,我们可以在结构体里面根据解题的需要定义相应的变量,
字典树给出abcd,abd,bcd,efg,hi等这样的几个字符串,我们就建立这样的一棵树,最上面是root节点,它是一个空的节点,在root节点下面有很多节点,如果我们是只是小写的字符串的话,我们就可以设置26个节点,但是怎样把他们连起来呢,看到箭头我们就能想到用链表了,既上面的每一个字母都是一个节点,我们可以在结构体里面根据解题的需要定义相应的变量,
下面用一道可以作为字典树的模板题进行分析,题目地址:http://acm.nyist.net/JudgeOnline/problem.php?pid=290,题意就是给你n个字符串,让你统计出现最多次数的字符串,当然我们可以用其他的比较快的方法如vector容器或者map容器进行比较,但是最快的还是字典树,字典树的思路就是初始每个节点count的值为0,然后读入每个字符串建立字典树,建立的同时将最后一个字母的count值+1,这样我们只要找每读入一个字符串之后判断最后的count最大的记录下来就可以了,当然其这个结构的特殊性决定了它的高效。下面贴这个题的代码,可以作为一个模板代码:
#include <cstdio>
#include <cstdlib>
#include <cstring>
int max;
char ans[110];
struct tree //字典树每个节点
{
int count;
struct tree *next[26];
};
tree *root;
tree *newset() //用动态建树是开辟内存
{
tree *p;
p=(struct tree *)malloc(sizeof(struct tree));
for(int i=0;i<26;i++)
{
p->next[i]=NULL;
}
p->count=0;
return p;
}
void insert(char *s) //建立字典树,并判断出现最多的次数记录
{
tree *p;
p=root;
int len=strlen(s);
for(int i=0;i<len;i++)
{
if(p->next[s[i]-'a']==NULL)
p->next[s[i]-'a']=newset();
p=p->next[s[i]-'a'];
}
p->count++; //到最后一个节点才自加1;
if(p->count>max) //判断次数
{
max=p->count;
strcpy(ans,s);
}
}
int main()
{
int T;
char str[20];
root=newset();
scanf("%d",&T);
while(T--)
{
scanf("%s",str);
insert(str);
}
printf("%s %d\n",ans,max);
return 0;
}
当然有的题可能会需要我们再次遍历树查找某些值,树的遍历我们可以根据建树来写,也是从root节点开始,根据题目需要边判断边遍历,记录。下面是一个遍历的函数,可做参考:
int findTrie(char *str)
{
int len = strlen(str);
Trie *p = root;
for(int i=0; i<len; ++i)
{
int id = str[i]-'0';
p = p->next[id];
if(p == NULL)
return 0;
if(p->v == -1)
return -1;
}
return -1;
}
有时候让我们需要处理多组数据的时候,需要清空内存判断下一组数据,当然也是从root节点往下清理的。函数:
int deal(Trie* T) //这是把T清空
{
int i;
if(T==NULL)
return 0;
for(i=0;i<10;i++)
{
if(T->next[i]!=NULL)
deal(T->next[i]);
}
free(T);
return 0;
}
好了,就到这里了,等学了字典树的排序再来更新、、、