poj1556

计算几何+最短路

最短路是套的模版。。= =

毕竟不是自己写的。。模版上的点竟然是从0开始的。

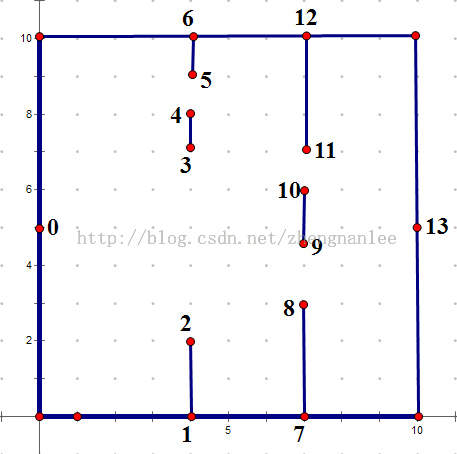
难在建图。图中，比如2和12点，其间如果没有任何线段阻挡，那么边权是他们的直线距离，如果有线段阻挡，边权是inf。

枚举每两个点，用其组成的线段与其他所有线段判断，如果相交则边权inf，如果不相交距离是其直线距离。

#include <iostream>
#include <math.h>

#define eps 1e-8
#define zero(x) (((x)>0?(x):-(x))<eps)

#define pi acos(-1.0)


struct point
{
	double x, y;
};

struct line
{
	point a, b;
};

//计算cross product (P1-P0)x(P2-P0)
double xmult(point p1, point p2, point p0)
{
	return (p1.x - p0.x)*(p2.y - p0.y) - (p2.x - p0.x)*(p1.y - p0.y);
}
//两点距离
double distance(point p1, point p2)
{
	return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y));
}

//判三点共线
bool dots_inline(point p1, point p2, point p3)
{
	return zero(xmult(p1, p2, p3));
}

//判点是否在线段上,包括端点
bool dot_online_in(point p, line l)
{
	return zero(xmult(p, l.a, l.b)) && (l.a.x - p.x)*(l.b.x - p.x) < eps && (l.a.y - p.y)*(l.b.y - p.y) < eps;
}

//判点是否在线段上,不包括端点
bool dot_online_ex(point p, line l)
{
	return dot_online_in(p, l) && (!zero(p.x - l.a.x) || !zero(p.y - l.a.y)) && (!zero(p.x - l.b.x) || !zero(p.y - l.b.y));
}

//判两点在线段同侧,点在线段上返回0
bool same_side(point p1, point p2, line l)
{
	return xmult(l.a, p1, l.b)*xmult(l.a, p2, l.b) > eps;
}

//判两点在线段异侧,点在线段上返回0
bool opposite_side(point p1, point p2, line l)
{
	return xmult(l.a, p1, l.b)*xmult(l.a, p2, l.b) < -eps;
}

//判两直线平行
bool parallel(line u, line v)
{
	return zero((u.a.x - u.b.x)*(v.a.y - v.b.y) - (v.a.x - v.b.x)*(u.a.y - u.b.y));
}

//判两直线垂直
bool perpendicular(line u, line v)
{
	return zero((u.a.x - u.b.x)*(v.a.x - v.b.x) + (u.a.y - u.b.y)*(v.a.y - v.b.y));
}

//判两线段相交,包括端点和部分重合
bool intersect_in(line u, line v)
{
	if (!dots_inline(u.a, u.b, v.a) || !dots_inline(u.a, u.b, v.b))
		return !same_side(u.a, u.b, v) && !same_side(v.a, v.b, u);
	return dot_online_in(u.a, v) || dot_online_in(u.b, v) || dot_online_in(v.a, u) || dot_online_in(v.b, u);
}
bool intersect_ex(line u, line v)
{
	return opposite_side(u.a, u.b, v) && opposite_side(v.a, v.b, u);
}

//单源最短路径,bellman_ford算法,邻接阵形式,复杂度O(n^3)
//求出源s到所有点的最短路经,传入图的大小n和邻接阵mat
//返回到各点最短距离min[]和路径pre[],pre[i]记录s到i路径上i的父结点,pre[s]=-1
//可更改路权类型,路权可为负,若图包含负环则求解失败,返回0
//优化:先删去负边使用dijkstra求出上界,加速迭代过程
#define MAXN 200
#define inf 1000000000
typedef double elem_t;

int bellman_ford(int n, elem_t mat [][MAXN], int s, elem_t* min, int* pre){
	int v[MAXN], i, j, k, tag;
	for (i = 0; i < n; i++)
		min[i] = inf, v[i] = 0, pre[i] = -1;
	for (min[s] = 0, j = 0; j < n; j++){
		for (k = -1, i = 0; i < n; i++)
			if (!v[i] && (k == -1 || min[i] < min[k]))
				k = i;
		for (v[k] = 1, i = 0; i < n; i++)
			if (!v[i] && mat[k][i] >= 0 && min[k] + mat[k][i] < min[i])
				min[i] = min[k] + mat[pre[i] = k][i];
	}
	for (tag = 1, j = 0; tag && j <= n; j++)
		for (tag = i = 0; i < n; i++)
			for (k = 0; k < n; k++)
				if (min[k] + mat[k][i] < min[i])
					min[i] = min[k] + mat[pre[i] = k][i], tag = 1;
	return j <= n;
}

int main()
{
	line l[100];
	point p[200];
	int n;
	while (std::cin >> n && (n != -1))
	{
		int j = -1;
		int k = 0;
		p[0].x = 0.0, p[0].y = 5.0;
		for (int i = 0; i < n; i++)
		{
			double a, b, c, d, e;
			std::cin >> a >> b >> c >> d >> e;
			l[++j].a.x = a, l[j].a.y = 0.0;
			l[j].b.x = a, l[j].b.y = b;

			l[++j].a.x = a, l[j].a.y = c;
			l[j].b.x = a, l[j].b.y = d;

			l[++j].a.x = a, l[j].a.y = e;
			l[j].b.x = a, l[j].b.y = 10.0;

			p[++k].x = a, p[k].y = 0.0;
			p[++k].x = a, p[k].y = b;
			p[++k].x = a, p[k].y = c;
			p[++k].x = a, p[k].y = d;
			p[++k].x = a, p[k].y = e;
			p[++k].x = a, p[k].y = 10.0;
		}
		p[++k].x = 10.0, p[k].y = 5.0;

		/*for (int i = 0; i <= j; i++)
		{
		std::cout << l[i].a.x << ' ' << l[i].a.y << " to " << l[i].b.x << ' ' << l[i].b.y << std::endl;
		}
		for (int i = 1; i <= k; i++)
		{
		std::cout << i << ' '<<p[i].x << ' ' << p[i].y << std::endl;
		}*/

		double mat[MAXN][MAXN];
		for (int a = 0; a <= k; a++)
		{
			for (int b = 0; b <= k; b++)
			{
				line temp;
				temp.a = p[a], temp.b = p[b];
				bool flag = false;
				for (int c = 1; c <= j; c++)
				{
					if (intersect_ex(temp, l[c]))
					{
						mat[a][b] = inf;
						flag = true;
						break;
					}
				}
				if (!flag)
				{
					mat[a][b] = distance(p[a], p[b]);
				}
			}
		}
		/*
		for (int a = 0; a <= k; a++)
		{
			for (int b = 0; b <= k; b++)
			{
				std::cout << a << ' ' << b << ' ' << mat[a][b] << '\n';
			}
		}
		std::cout << k << std::endl;*/
		
		elem_t min[MAXN];
		int pre[MAXN];
		bellman_ford(k+1, mat, 0, min, pre);
		/*for (int i = 0; i <= k; i++)
		{
			std::cout << ' ' << min[i] << "\n";
		}*/
		printf("%.2lf\n", min[k]);
	}
}