关于方程a^x=1(mod m)的最小x解
定理:
设gcd(a,m)=1,必有正整数x,使得a^x=1(mod m),且设满足等式的最小正整数为x0,必满足x0|phi(m).注意m>1.
否则如果gcd(a,m)!=1,则方程a^x=1(mod m)没有解。
典型题目:HDU1395,HDU3307,POJ3696
前面两题很简单,下面我们来分析POJ3696.
题目:The Luckiest number
题意:求出由全8组成的数的最短长度,使得给定的L能整除它。
分析:先分析公式,可以发现一个全由A组成的数的表示形式为: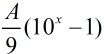 ,所以全8组成的数为:
,所以全8组成的数为: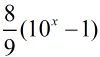 。
。
L能整除它,则有: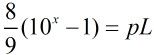 ,亦即:
,亦即:![]() ,则应该先约去8与9L的最大公约数。
,则应该先约去8与9L的最大公约数。
因为8与9互素,所以实际上就是约去8与L的最大公约数。
所以进一步有:![]() ,然后就是上面的那个定理了。
,然后就是上面的那个定理了。
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
using namespace std;
typedef long long LL;
LL dp[1000005];
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
LL phi(LL n)
{
LL rea=n,i;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
rea=rea-rea/i;
while(n%i==0) n/=i;
}
}
if(n>1)
rea=rea-rea/n;
return rea;
}
LL multi(LL a,LL b,LL m)
{
LL ans=0;
while(b)
{
if(b&1)
{
ans=(ans+a)%m;
b--;
}
b>>=1;
a=(a+a)%m;
}
return ans;
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans=1;
a%=m;
while(b)
{
if(b&1)
{
ans=multi(ans,a,m);
b--;
}
b>>=1;
a=multi(a,a,m);
}
return ans;
}
int main()
{
int k=1;
LL L,i,m;
while(cin>>L)
{
if(L==0) break;
printf("Case %d: ",k++);
m=9*L/gcd(8,L);
if(gcd(10,m)!=1)
{
puts("0");
continue;
}
LL ans=phi(m);
LL size=0;
for(i=1;i*i<=ans;i++)
{
if(ans%i==0)
{
dp[size++]=i;
if(ans!=i*i) dp[size++]=ans/i;
}
}
sort(dp,dp+size);
for(i=0;i<size;i++)
if(quick_mod(10,dp[i],m)==1) break;
cout<<dp[i]<<endl;
}
return 0;
}