可能是最难围住的神经猫——寻找必胜路径的算法实现

标题借鉴了一下老罗的风格，哈哈(*^__^*) 

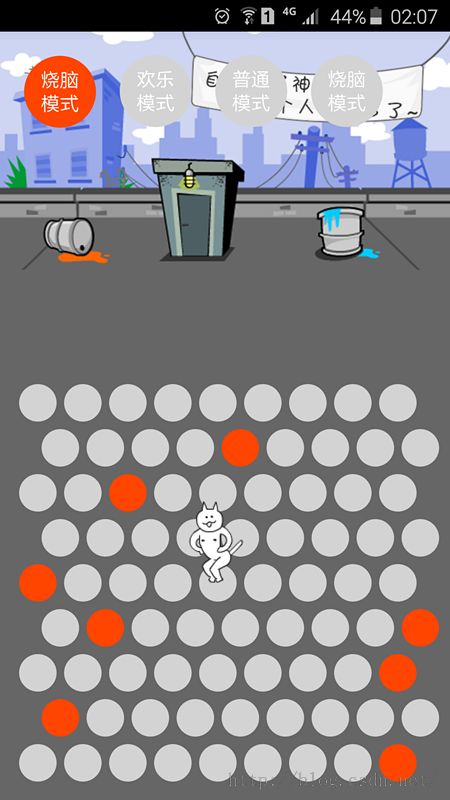
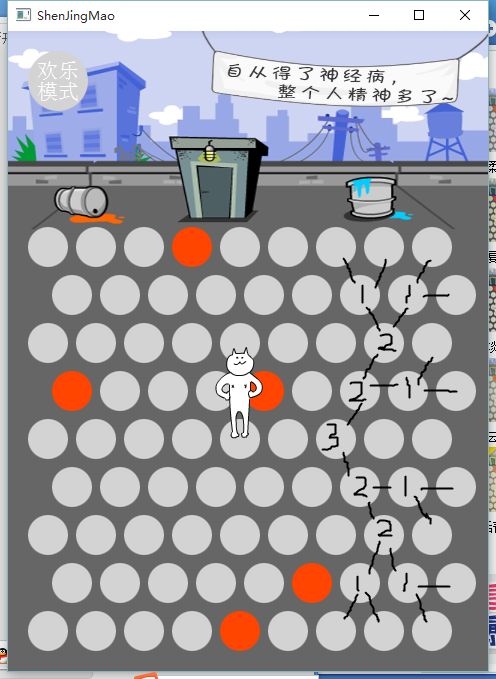
原来围住神经猫游戏刚火的时候，恰巧当时正在学QML，顺手就给弄了一个，不知道大家还记不记得这个游戏，简单说就是设置障碍把中间的猫围住就获胜了（橙色圆即为障碍），而猫可以向周围六个方向中的非障碍区域逃跑，如果猫逃跑到四周边界的圆上则玩家失败，界面是酱紫的：

然后在 Qt 贴吧里面也共享了一下：http://tieba.baidu.com/p/3241650033

因为当时做这个的时候主要是想练下 QML，所以草草弄了个随机方向选择算法（应该没资格叫算法吧...），然后这只小猫就蠢得不要不要的，到了边界都往回跑。。。

最近突然又翻到这个东西，就还是想把这个草率的东西弄得完整一点，于是又花了几天时间，先是增加了两个游戏难度，一个就是原版以及网络上大部分版本所使用的基于贪心法的实现，说直白点就是打表了，找到最短通路，然后朝那个方向跑。但是这个方式很容易被玩家使用“挖陷阱”的方式破掉，大部分“攻略”也是基于此的。第二个就是这篇博文的主题了——这个游戏人类几乎无法取胜。不过我们后头来谈，这里先把嗑唠完O(∩_∩)O~

之后呢，为了在手机也可以玩这个游戏，调整了界面布局以适应不同屏幕尺寸，然后就有了下面这个apk：

http://pan.baidu.com/s/1eQ0ePhg，下面上个图，上排多了难度选择的内容。

为毛apk要放百度网盘呢，原本也是想试试这个小游戏能不能在百度91助手和豌豆荚上线，毕竟良心应用，无须任何权限且免费无广告。不过最后还是因为copyright的问题没能成功，想想也是，毕竟除了代码是自己写的，其它的都是用的人家的东西-.-

然后这个小游戏也托管在Github上，如果大家有兴趣也可以共同维护一下：

https://github.com/uCloudCastle/ShenJingMao

好，再唠下去就成单口相声了，赶快开始我们的正片部分：

我们可以再看一眼上面的三个难度选择，“欢乐模式”就是随机方向了，“普通模式”就是贪心法+最大通路算法，这个算法在大多数情况下都比较好用，但如果是下面这样：

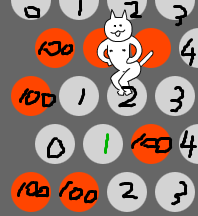
每一个边界上的数字表示从该点到边界需要的步数，障碍值我们直接设100了，因为总共也就81个点，当然这个100用一个const全局量来表示，以及地图的维度，尽量保证代码的通用性。

除了边界值和障碍值，其他点上的数字则是周围6个点数值中的最小值+1，有了这样一个矩阵，神经猫在移动时只需要往身边值最小的格子上移动就可以了。

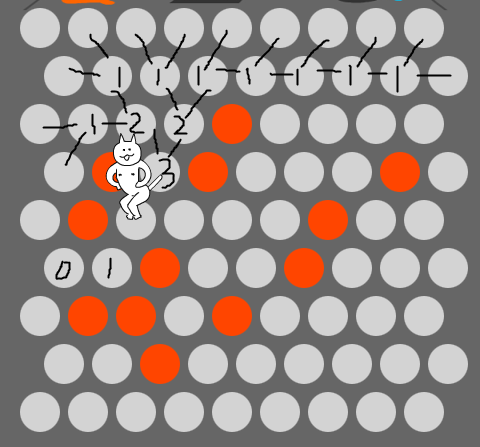
所以，“挖陷阱”捉神经猫的方法就是：现在玩家封上“1”为绿色的那个格子，神经猫只会向左侧的“1”移动，然后玩家封上“0”，神经猫后退到“2”，玩家再封“3”，就 GameOver 了。

现在的问题就是，如果让神经猫能够知道玩家在封绿色“1”那个格子的时候是在“make trap”呢，或者说，看起来充满诱惑的路到底该不该走？

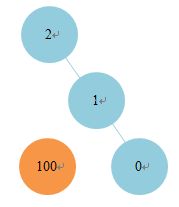
如上图，如果当前轮到神经猫移动，而猫在“2”的位置，“1”的周边仅有那一个值为“0”的边界点，神经猫能移动到“1”处吗？答案是取决于“1”周边其他格子的数值，但稍微理智点的玩家应该都不会让猫从这个“0”出去，所以，神经猫最终要取胜，一定是踏上了某个拥有两个“0”值边界的节点：

此时，神经猫在“E1”处，玩家无论封住哪个“0”都无法阻止神经猫逃出，我们把这样的“1”节点命名为“E1”。也就说，如果神经猫到达“E1”，它就已经赢了。那么同样的，如果神经猫到达“E2”，结局也就写好了（当然也包含超过两个“E1”的情况）：

注意这里我们再把开始那个“周围只有一个边界的格子”的问题再处理一下：

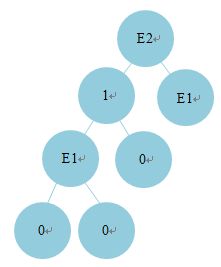
这个“1”周围只有一个出口，但当神经猫到达该点时，玩家势必要将它身边这个“0”封住，然后神经猫也就能够顺利到达“E1”了，也就是说，这个“1”等同于身边最小的“Ex”，所以在其之上的“E2”也就成立了。

对于这个情况有一个更一般的推论：如果把边界“0”看做“E0”，那么两个“Ex”(x代表任一数字)的父节点为两者中的较大值，也就是说，下面这个图是成立的：

到了这里问题似乎变得很明了，我们继续向上推到“E3”、“E4”。。只要神经猫踏上其中的任何一个点，游戏其实就已经结束了，但是，在这个map中，大多数结构是下面这样的：

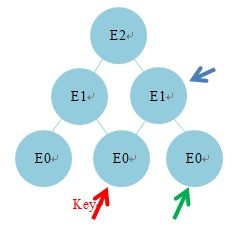
有一个边界被两个“E1”共享，如果 cat 目前位于“E2”，玩家稍微聪明点不去封其中一个“E1”，而是封住了红色箭头所指向的关键边界点Key，那么无论神经猫到达哪个“E1”，玩家都可以将其截住。（比如神经猫走到蓝色箭头处，而玩家再封住绿色箭头所指节点。）

因此，我们需要保证该拓扑是一个真正的树形结构，每个节点的子节点不能被其他成员共享。在9*9并且包含障碍节点的map中，如果我们想从边界点开始建立完全由独立互不影响的“E1”、 “E2”、 “E3”。。构成的树形网络，一方面是计算量特别大，因为每个边界“0”点换到一个新的“E1”名下都会从下至上影响每一层的计算，另一方面是，该map的结构决定了能够作为“E3”的点也就那么几个，“E4”就不用想了，下图显示了需要多少个非障碍节点才能构成一个“E3”节点。

因此，从神经猫所在的节点向外扩张反而是更好的选择，即便神经猫当前不在“必胜路径上”，玩家要想识别出每条通往“E3”、“E2”和“E1”的路径并破坏它却并不容易，我们使用一个多叉树的结构来存储神经猫的路径，为了保证节点不会反向跳到自己的祖辈造成无限循环，这里按层次遍历方式建树，并用 QHash 存储祖辈及其所在层数。各节点的子节点与其兄弟节点的子节点可能相同，这样保证了神经猫在比较靠近中心或者障碍较多的位置仍然能够找到一条非“必胜”但仍较优的路径，玩家稍微下错一步，该路径可能就成为“必胜”路径了。

所用到的数据结构是下面这个样子的：

struct TreeNode {
    int val;
    int depth;
    QVector<TreeNode*> childList;

    TreeNode(int v = nullInit, int d = nullInit) :
    val(v), depth(d){}

    ~TreeNode()
    {
        TreeNode* n;
        foreach(n, childList)
            delete n;
    }
};

struct PathStruct {
    QHash<int, int> m_Hash;
    TreeNode *m_Node;

    PathStruct() { m_Node = NULL; }
    ~PathStruct() { delete m_Node; }
};

呼，更多的细节大家可以到上面贴的 Github 上看看，只要想法到了代码反而是其次了，最后给大家留个图吧，猜猜神经猫会往哪儿跑呢？~