LeetCode(50) N-Queens II
题目如下:
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.
For example,
There exist two distinct solutions to the 4-queens puzzle:
[
[".Q..", // Solution 1
"...Q",
"Q...",
"..Q."],
["..Q.", // Solution 2
"Q...",
"...Q",
".Q.."]
]
Now, return the total number of distinct solutions.
分析如下:
这道题目我一直想得不是很明白,直到今天看了一个princeton的课件,才发现好像有点真正理解这个问题了。
第一步,先会写permutation.
写permutation的经典做法是DFS, 核心代码在这里
void dfs(vector<int> & num, int k, int n, vector<vector<int> > & result) {
if (k == n){
result.push_back(num);
}else {
for (int i = k; i <= n; ++i) { //i = k, i与包含自己在内的后面的所有元素进行交换。
swap(num, k, i);
dfs(num, k+1, n, result);
swap(num, k, i);
}
}
}
第二步,把2D棋盘简化为1D的数组,比如a[3] = 5,表示在第3行和第5列放一个棋子。
第三步,继续用1D数组表示棋盘,接下来需要满足两个条件。条件①,不能在棋盘相同行放皇后条件,条件②不能在棋盘相同列放皇后的要求,很容易发现,这道题需要你求1~8的一个排列,并且这个排列需要满足前面的条件①, 条件②。
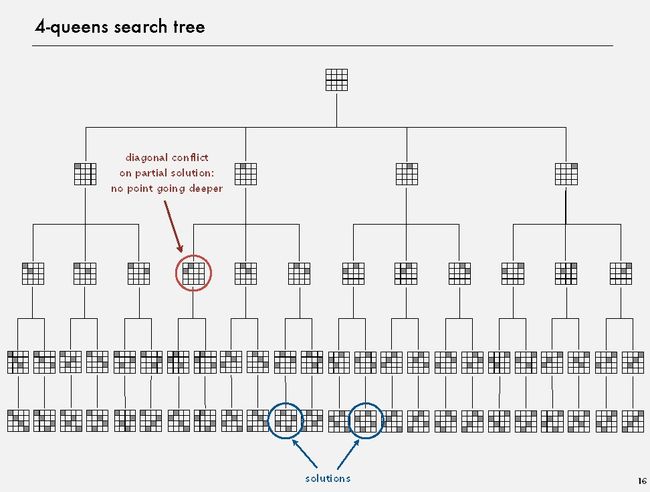
第三步,除了满足条件①, 条件②,还需要满足一个条件,对角线不能冲突。见下图
第四步,把对角线冲突的排列组合过舍弃。这个舍弃不能等到所有可能的排列的结果都出来了再进行,这样的话,N的数讲用掉N!的时间按复杂度才能进行检查和舍弃。必须在生成排列的中间过程中一边舍弃一边生成。这就是backtracking。见下图。
第五步,知道走到正常的DFS求排列的结束条件时,结束。
我的代码:
//3ms nice!
class Solution {
public:
void swap(int* array, int a ,int b) {
int tmp = array[a];
array[a] = array[b];
array[b] = tmp;
}
bool collide(int k, int* array) {
for (int i = 0; i <k; ++i) {
//检查array[k] 和 array[k]之前的数有无对角线方向的冲突
if ((array[k] - k == array[i] - i) ||
(array[k] + k == array[i] + i))
return true;
}
return false;
}
void GenQueens(int k, int n, int & sum, int* array) {
if (k == n){
sum++;
return;
} else {
for (int i = k; i < n; ++i) {
swap(array, i, k);
//如果交换后的当前值引起了冲突,就不进行下一步的dfs
if(!collide(k, array)) {
GenQueens(k+1, n, sum, array);
}
swap(array, k, i);
}
}
}
int totalNQueens(int n) {
int* array = new int[n];
for (int i = 0; i < n; ++i) {
array[i] = i;
}
int sum = 0;
GenQueens(0, n, sum, array);
delete [] array;
return sum;
}
};