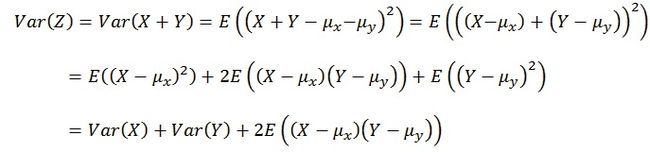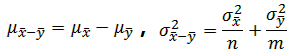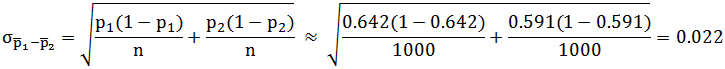Khan公开课 - 统计学学习笔记:(八)样本均值之差
E(X)和Var(X)符合线性
所谓的线性,就是f(x+y)=f(x)+f(y)。概率中期望值和方差都符合线性。
X、Y为两个互不相干,即相互独立的概率变量。
如果Z=X+Y,则E(Z)=E(X+Y)=E(X)+E(Y),方差Var(Z)=Var(X+Y)=Var(X)+Var(Y)。
如果A=X-Y,则E(A)=E(X-Y)=E(X)-E(Y),方差Var(A)=Var(X-Y)=Var(X)+Var(Y)。因为Var(-Y)=Var(Y)。
下面我们试图进行证明。
Var的线性证明要复杂一些。
对于等式右边的第三个参数相当于2E((X-E(X))(Y-E(Y)),其中E((X-E(X))(Y-E(Y))也记为Cov(X,Y),即协和方差,当X和Y完全独立的时候,Cov(X,Y)=0。因此,在X、Y为完全不相干事件的前提下,证得Var(Z)=Var(X)+Var(Y),符合线性关系。我们换种方法证明一下,所谓不相关,就是在不同的纬度上,即矢量相互垂直,用勾股定理证明。Z2=X2+y2,由于E(X)符合线性关系E(Z2)=E(X2)+E(y2)
对于Var(A)=Var(X-Y)=Var(X)+Var(Y),由于Var(X-Y)=Var(X)+Var(-Y),只要能证明Var(-Y)=Var(Y)即可。
注意其中E(-Y)=-E(Y),当Y成为都取相反值时,mean也成了相反值,因此方差不发生变化。
样本均值之差的例子1
Z=X-Y,根据中心极限定理,有:
样本均值之差有很多应用场景。例如测试药品效果,实验组n1=100,E(X1)=9.31,S1=4.76,另一个是对照组,n2=100,E(X2)=7.40,S2=4.04。
(1)估算试验效果95%的置信区间。
有两个sample size=100的均值样本变量:X1和X2,药物的效果Y=X1-X2,而X1和X2是独立的样本,即不相干两个变量:X1和X2,试验效果Y=X1-X2,有:
E(Y)=E(X1-X2)= E(X1)-E(X2)≈9.31-7.40=1.91
我们查Z table,得到z=1.96
P(Y is within ±1.96σY of μY)=95%
P(1.91 is within ±1.21 of μY) = 95%
P(μY is within ±1.21 of 1.91) = 95% ,药物效果95%的置信区间为(0.7,3.12)。
(2)在sinificance level α=5%下,是否认为药物具有效果?
H0:μx1-μx2= 0,即μx1-x2=0
H1:μx1-μx2 > 0,即μx1-x2>0,是个单边检验
由于样本足够大,采用Z table,注意此例为one tailed test,差得z score=1.65,而标准差为
我们计算的1.65×0.617=1.033。而本例中9.31-7.40=1.91,也就是我们将选择H1。
样本均值之差的例子2:总本占比的比较
均值样本支持的应用范围非常广泛,在这个例子中比较男选民投票和女选民投票的差异。在抽样的1000个男选民中投个某候选人A的票给642,其余投个另一个候选人B,在抽样的1000名女选民中,投个候选人A的有591票,其余投給候选人B。上面是已知条件,读题如下:
男选民:Bernoulli分布,有μ1=p1,和σ12=p1(1-p1)。在n=1000个抽样中,样本均值为![]() ,其中这次样本均值采样为p1=0.642
,其中这次样本均值采样为p1=0.642
女选民:Bernoulli分布,有μ2=p2,和σ22=p2(1-p2)。在n=1000个抽样中,样本均值为![]() ,其中这次样本均值采样为p2=0.591
,其中这次样本均值采样为p2=0.591
(1)问:男、女选民投给候选人A的差异的95%的confident interval
即求p1-p2的95%置信区间。
对于男女选民的样本均值的之差异有: ![]() ,我们得到其中一个样本均值之差为0.642-0.591=0.051。
,我们得到其中一个样本均值之差为0.642-0.591=0.051。
对于男女选民的样本均值的标准差有:
求p1-p2的95%置信区间,即求95% chance that p1-p2 is within distance of 0.051,等同于95% chance that 0.051 is within d of p1-p2,即P(0.051 is within d of p1-p2)=95%,查z table得α=1.96,男女候选人投给被选人A的差异p1-p2的95%置信区间为(0.08,0.94)
(2)问:在α=5%下,男、女选民投给候选人A是否存在差异
H0:No difference, p1=p2 →p1-p2=0
H1: There is difference, p1≠p2 → p1-p2≠0
假设H0是正确的→![]() ,样本均值之差为
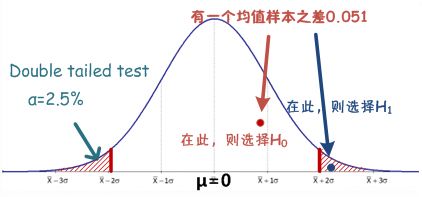
,样本均值之差为![]() ,如图,我们需要知道0.051的概率落在那个区间。
,如图,我们需要知道0.051的概率落在那个区间。
H0的假设是p1=p2=p,因此样本均值之差的标准差的更好估算应该是
而p在2000个样本中去均值更为准确,p=(642+591)/2000=0.6165,计算的σ=0.0217。
样本均值之差的z score=0.051/0.0217=2.35,我们知道在双边检测的整体分布中,α=5%的critical z score=1.96,所有这个样本均值之差位于更为极端的区间,在统计上,在α=5%上,认为男女选民存在差异,即选择H1。
相关链接:我的四方书库